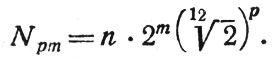Алгебра что такое ноты

Логарифмы в музыке

Музыканты редко увлекаются математикой; большинство их, питая к этой науке чувство уважения, предпочитает держаться от нее подальше. Между тем музыканты — даже те, которые не проверяют, подобно Сальери у Пушкина, «алгеброй гармонию», — соприкасаются с математикой гораздо чаще, чем сами подозревают, и притом с такими страшными вещами, как логарифмы.

Позволю себе по этому поводу привести отрывок из статьи нашего покойного физика проф. А. Эйхенвальда * .

* ( Она была напечатана в «Русском астрономическом календаре на 1919 г.» и озаглавлена «О больших и малых расстояниях».)

«Товарищ мой по гимназии любил играть на рояле, но не любил математики. Он даже говорил с оттенком пренебрежения, что музыка и математика друг с другом ничего не имеют общего. «Правда, Пифагор нашел какие-то соотношения между звуковыми колебаниями, — но ведь как раз пифагорова-то гамма для нашей музыки и оказалась неприменимой».

Представьте же себе, как неприятно был поражен мой товарищ, когда я доказал ему, что,, играя по клавишам современного рояля, он играет, собственно говоря, на логарифмах. И действительно, так называемые «ступени» темперированной хроматической гаммы не расставлены на равных расстояниях ни по отношению к числам колебаний, ни по отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин. Только основание этих логарифмов равно 2, а не 10, как принято в других случаях.

Положим, что нота do самой низкой октавы — будем ее называть нулевой октавой — определена n колебаниями в секунду. Тогда do первой октавы будет делать в секунду 2n колебаний, а m-й октавы n × 2 m колебаний и т. д. Обозначим все ноты хроматической гаммы рояля номерами p, принимая основной тон do каждой октавы за нулевой; тогда, например, тон sol будет 7-й, la будет 9-й и т. д.; 12-й тон будет опять do, только октавой выше. Так как в темперированной хроматической гамме каждый последующий тон имеет в 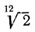большее число колебаний, чем предыдущий, то число колебаний любого тона можно выразить формулой

Логарифмируя эту формулу, получаем:

а принимая число колебаний самого низкого do за единицу (n = 1) и переводя все логарифмы к основанию, равному 2 (или попросту принимая lg 2 = 1), имеем:

Отсюда видим, что номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков * . Мы даже можем сказать, что номер октавы представляет собой характеристику, а номер звука в данной октаве ** — мантиссу этого логарифма».

* Умноженные на 12.

Например, — поясним от себя, — в тоне sol третьей октавы, т. е. в числе 3 + 7/12 (≈ 3,583), число 3 есть характеристика логарифма числа колебаний этого тона, a 7/12 (≈ 0,583) — мантисса того же логарифма при основании 2; число колебаний, следовательно, в 2 3,583 , т. е. в 11,98, раза больше числа колебаний тона do первой октавы.

Источник

Урок 2. Нотная грамота

Теория музыки невозможна без нотной грамоты. В этом вы уже успели убедиться, когда изучали на первом уроке ступени звукоряда. Вы уже знаете, что основным ступеням звукоряда присвоены те же названия, что и нотам, и понимаете что такое понижение ступени, т.е. ноты.

Этого достаточно, чтобы приступить к изучению нотной грамоты «с нуля». Если нотная грамота вам знакома, все равно просмотрите материал урока с целью убедиться, что вы ничего не пропустили, когда изучали нотную грамоту ранее.

Это нужно, чтобы вы могли в будущем самостоятельно разбирать ноты, записанные на нотном стане, и ориентироваться в табах и аккордах, если вам попадется аккордовая запись мелодии либо табулатура.

Содержание:

Заметим, что большинство современных музыкальных сайтов чаще предлагают для гитары именно аккорды либо табулатуру (табы) к песне, нежели традиционную запись на нотном стане. Для начинающих музыкантов нужно уточнить, что аккорды и табы – это те же самые ноты, только записанные в другом виде, т.е. в другом виде музыкальной нотации, поэтому выучить ноты нужно обязательно. В общем, приступаем!

Кто придумал ноты

Начнем с небольшого исторического экскурса. Считается, что первым человеком, кому пришла в голову идея обозначать высоту звука знаками, был флорентийский монах и композитор Гвидо д’Ареццо. Это случилось в первой половине 11 века. Гвидо учил монастырских певчих различным церковным песнопениям, а чтобы добиться слаженного звучания хора, придумал систему знаков, указывающих на высоту звука.

Это были квадратики, расположенные на четырех параллельных линиях. Чем более высокий звук нужно было издать, тем выше располагался квадратик. В его нотации было всего 6 нот, а названия они получили от начальных слогов строк Гимна, воспевающего Иоанна Крестителя: Ut, Resonare, Mira, Famuli, Solve, Labii. Несложно заметить, что 5 из них – «ре», «ми», «фа», «соль», «ля» – используются и сегодня. К слову, музыку к гимну написал сам Гвидо д’Ареццо.

Позже в нотный ряд добавилась нота «си», в нотный стан – пятая линейка, скрипичный и басовый ключи, знаки альтерации, которые мы сегодня будем изучать. В эпоху Средневековья, когда зарождалась буквенная нотация, звукоряд было принято начинать с ноты «ля», за которой закрепилось обозначение в виде первой буквы латинского алфавита А. Соответственно, следующей за ней ноте «си» досталась вторая буква алфавита В.

Современное понимание звукоряда и основных его ступеней сложилось в 17 веке, а звук, соответствующий по высоте «си-бемолю», долгое время считался базовым элементом музыкальной системы, т.е. не пониженным и не повышенным. Сегодня общепринятой считается система нотации в виде C, D, E, F, G, A, B. Хотя и обозначение ноты «си» в виде Н тоже можно встретить. Мы уже начали и далее продолжим изучать системы нотации и записи нот на нотном стане, принятые в современном мире музыки.

Расположение нот на нотном стане

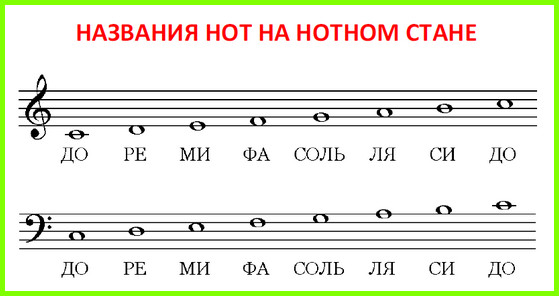
Вы уже знаете, что нота – это музыкальный звук. Ноты отличаются по высоте, и за каждой нотой закреплено свое обозначение. Также вы уже поняли, что нотный стан представляет собой 5 параллельных линий, на которых расположены ноты. За каждой нотой закреплено свое место. Собственно, именно так и можно идентифицировать ноты, глядя на обозначения в нотном стане. Теперь давайте совместим эти знания и посмотрим, как выглядит нотный стан с нотами в самом общем виде (на значки слева пока не смотрим):

Нотный стан (он же нотоносец) – это те самые 5 параллельных линий, которые вы видите на картинке. Кружочки на нотах – это условные обозначения нот. На верхнем нотоносце вы видите ноты для 1-й октавы, на нижнем – ноты для малой октавы.

Точкой отсчета в обоих случаях является нота «до» 1-й октавы, и для нее предусмотрена добавочная линейка. Разница в том, что на верхнем нотоносце ноты идут снизу вверх, поэтому нота «до» 1-й октавы находится внизу. На нижнем нотоносце ноты идут сверху вниз, поэтому нота «до» 1-й октавы находится сверху.

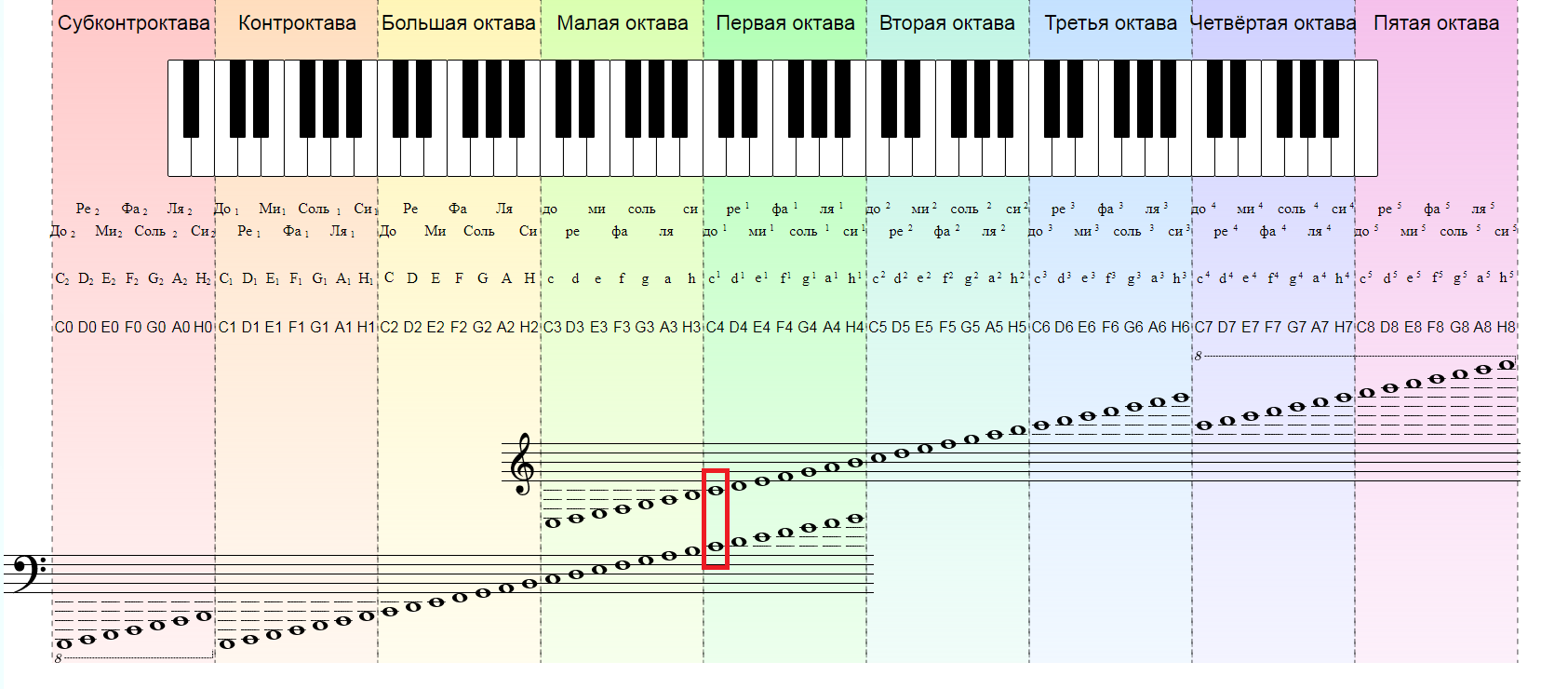
Однако мы помним, что музыкальные звуки охватывают намного больший диапазон, чем малая и первая октавы. Поэтому, чтобы получить полное представление о расположении нот на нотном стане, вам нужно изучить более подробную схему размещения нот:

Самые внимательные из вас увидели, что и на подробной схеме мы видим не все октавы. Чтобы увидеть правильное расположение всех нот, нам снова понадобятся добавочные линейки. Посмотрите, как это выглядит, на примере контроктавы:

А теперь вы уже готовы к тому, чтобы выучить расположение всех нот на нотном стане. Для удобства скоординируем изображение нотного стана с клавиатурой фортепиано, которую вы уже успели рассмотреть, когда проходили урок №1. Обратите внимание, где находится первая нота «до» 1-й октавы относительно линий верхнего и нижнего нотоносца. Мы отметили ее красным цветом:

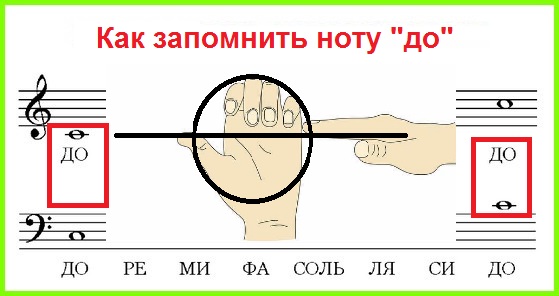
У большинства из тех, кто видит всю эту картину впервые, возникает вопрос: а как же это запомнить. В общем-то, запомнить вам нужно только расположение первой ноты «до» 1-й октавы, а все остальные ноты располагаются в определенной логической последовательности относительно первой ноты «до».

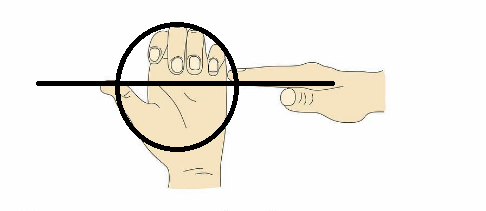
Более легкому запоминанию нот поможет упражнение «Лезгинка». Как ни удивительно, к музыке оно никакого отношения не имеет, а предназначено для развития координации работы правого и левого полушарий головного мозга у детей [А. Сиротюк, 2015]. Представьте, что кулак или ладошка с поджатыми пальцами – это кружок для обозначения ноты, а прямая кисть руки, которая упирается в середину ребра ладони – это добавочная линейка нотоносца:

Так вы запомните, что добавочная линейка рассекает пополам кружок, обозначающий ноту «до»:

Дальше будет проще. Ноту «ре» можно представить как кулак, расположенный над вытянутой кистью. Следующая нота «ми» будет рассечена пополам вытянутой кистью, но кисть уже будет изображать не добавочную линию, а нижнюю из пяти линий нотоносца. Для ноты «фа» мы поднимаем кулак над линией, а ноту «соль» рассекаем вытянутой кистью, которая теперь изображает вторую снизу линию нотоносца. Думается, принцип построения нот вы поняли. Аналогично можно выстроить ноты, идущие вниз относительно «до» 1-й октавы.

Есть и другие мнемонические техники запоминания. «Рассеченные» ноты на нотном стане можно запомнить по первым буквам английской фразы Every (Е-«ми») Good (G-«соль») Boy (В-«си») Does (D-«ре») Fine (F-«фа»). Ноты, обозначенные цельными не «рассеченными» кружочками можно запомнить с помощью слова FACE: (F-«фа»), (А-«ля»), (С-«до»), (Е-«ми»).

Если вы хотите освоить специальные мнемотехники, которые помогут запоминать любую информацию, записывайтесь на наш курс «Мнемотехники», и за короткий срок (чуть больше месяца) вы поймете, что никаких проблем с памятью у вас нет. Есть лишь более эффективные техники запоминания, нежели те, которыми вы пользовались ранее.

Итак, с расположением нот на нотном стане, думаем, в целом все понятно. Самые внимательные уже заметили, что при такой расстановке нот места для диезов и бемолей, т.е. повышения и понижения ноты, уже не остается. И вот для этого нам нужны знаки альтерации в нотах.

Знаки альтерации

В конце предыдущего урока вы уже выучили символы диеза (♯) и бемоля (♭). Вы уже поняли, что если нота повышается на полутон, к ней добавляют значок диеза, если понижается на полутон – значок бемоля. Так, повышенная нота «соль» будет записана как G♯, а пониженная нота «соль» как G♭. Диез и бемоль называются знаками альтерации, т.е. изменения. Слово происходит от позднелатинского alterare, что переводится как «изменять».

Повышение на 2 полутона обозначается двойным, т.е. дубль-диезом, понижение на 2 полутона обозначается двойным, т.е. дубль-бемолем. Для дубль-диеза есть специальный значок, похожий на крестик , но, т.к. его трудно подобрать на клавиатуре, может использоваться обозначение ♯♯ или просто две решетки ##. Чтобы обозначить дубль-бемоль, пишут либо 2 значка ♭♭, либо латинские буквы bb.

Чтобы обозначить повышение или понижение ноты на нотном стане, значок диеза или бемоля располагается либо непосредственно перед нотой, либо, если ту или иную ноту нужно снизить или повысить во всем произведении, в начале нотного стана с нотами к произведению. Для случаев, когда изменение ноты предусмотрено на протяжении всего произведения, за символами диезов и бемолей закреплены определенные места на нотном стане:

Уточним для надписи на картинке, что под словосочетанием «в скрипичном ключе» подразумевается нотоносец для нот 1-5 октав, а под словами «в басовом ключе» – нотоносец для всех остальных октав от малой до субконтроктавы. Чуть позже мы расскажем про скрипичный и басовый ключи подробнее. Пока поговорим о том, как запомнить расположение диезов и бемолей на нотоносце.

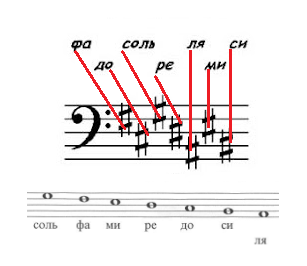
В принципе, это несложно, если вы успели выучить расположение значков, обозначающих ноты. Так, значок диеза располагается ровно на той линии нотоносца, что и та нота, которую требуется повышать. Для нотоносца в скрипичном ключе вам нужно запомнить, где находятся ноты в диапазоне от «ля» 1-й октавы до «соль» 2-й октавы, и вы легко поймете закономерность размещения диезов:

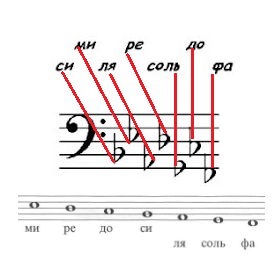
Точно такая закономерность наблюдается при расположении бемолей. Они тоже находятся на тех строчках, что и ноты, к которым они относятся. Здесь в качестве ориентира используются ноты в диапазоне от «фа» 1-й октавы до «ми» 2-й октавы:

С диезами и бемолями в басовом ключе действуют абсолютно те же закономерности. Для ориентирования в диезах вам следует запомнить расположение нот от «соль» малой октавы до «ля» большой октавы:

Для ориентирования в бемолях нужно запомнить расположение нот от «ми» малой октавы до «фа» большой октавы:

Как вы уже заметили, для расположения диезов и бемолей в начале произведения возле ключа – скрипичного или басового – задействуются только основные линейки нотоносца. Такие знаки альтерации называются ключевыми.

Знаки альтерации, относящиеся только к одной ноте, называются случайными или встречными, действуют в пределах одного такта и располагаются непосредственно перед этой нотой.

А сейчас давайте разберемся, что же делать, если нужно отменить диез или бемоль, установленный в начале нотного стана. Такая необходимость может возникнуть при модуляции, т.е. при переходе в другую тональность. Это модный прием, часто применяемый в эстрадной музыке, когда последний припев или куплет и припев исполняется на 1-2 полутона выше, чем предыдущие куплеты и припевы.

Для этого существует еще один знак альтерации: бекар. Его функция – отмена действия диезов и бемолей. Бекары тоже подразделяются на случайные и ключевые.

Функции бекара:

Случайный бекар отменяет действие случайных знаков альтерации, ставится в том месте и перед той нотой, для которой нужно отменить действие диеза или бемоля, и действует в пределах такта.
Ключевой бекар отменяет действие диезов и бемолей, указанных в начале произведения, т.е. ключевых. Он действует до следующей смены ключевого знака либо, если такового не будет, до конца произведения.

Чтобы было нагляднее, посмотрите, где располагается случайный бекар на нотном стане:

А теперь посмотрите, где располагается ключевой бекар, и вы сразу поймете разницу:

Уточним, что запись на нотном стане применяется для гитары и фортепиано, и любых других музыкальных инструментов, а вот табы, которые вы видите на предыдущей картинке под нотным станом, используются для гитары.

В гитарных табах 6 линий по количеству струн гитары. Верхняя линия обозначает самую тонкую струну, которая будет нижней, если вы возьмете гитару в руки. Нижняя линия означает самую толстую гитарную струну, которая является верхней, когда вы держите гитару в руках. Цифры указывают, на каком ладу зажимать ту струну, на которой написана цифра.

Применительно к иллюстрации по случайному бекару мы видим, что сначала нужно было играть «до-диез», который как раз находится на втором ладу 2-й струны. После бекара, т.е. отмены диеза, нужно играть чистую ноту «до», которая находится на первом ладу 2-й струны. Финальный урок нашего курса будет посвящен игре на различных музыкальных инструментах, в том числе на гитаре, и мы расскажем, как легко и просто запомнить расположение нот на гитарном грифе.

Подведем итог и сведем воедино всю информацию по знакам альтерации на следующей картинке:

Если вы уже умеете играть на каком-нибудь музыкальном инструменте, а сейчас решили подтянуть теорию, рекомендуем прочитать параграф 11 «Знаки альтерации» в учебнике Варфоломея Вахромеева «Элементарная теория музыки», где есть примеры разбора нотной записи [В. Вахромеев, 1961]. Мы же переходим к выполнению ранее данных обещаний и расскажем, что же такое ключи применительно к нотному стану.

Ключи на нотном стане

Мы ранее использовали словосочетания «в скрипичном ключе» и «в басовом ключе». Расскажем, что имеется в виду. Дело в том, что за каждой из линий нотоносца условно закреплена определенная звуковысотность. Ввиду того, что в мире существует множество музыкальных инструментов, издающих самые разные звуки, понадобились некие «точки отсчета» звуковысотности, и их роль отдали ключам.

Ключ выписывается так, чтобы линия, откуда стартует отсчет, пересекла его в главной точке. Таким способом ключ закрепляет за нотой, написанной на данной линии, точную высоту, относительно которой отсчитывается высотность и наименования прочих звуков. Различают несколько разновидностей ключей.

Ключи – перечень:

Скрипичный – так называемый ключ «Соль», закрепляет на 2-й линии высоту звука «соль» 1-й октавы. Главная точка расположена по центру спирали ключа и как бы «накручивается» на 2-ю линейку нотного стана.
Басовый– так называемый ключ «Фа», закрепляет на 4-й линии высоту «фа» в малой октаве. 2 точки знака стоят сверху и снизу 4-й линии нотоносца, если вести отсчет снизу.
Альтовый – так называемый ключ «До», закрепляет высоту «до» в 1-й октаве на 3-й линии, используется преимущественно для альтовых инструментов.
Теноровый – тоже ключ «До», но уже на 4-й линии, используется для таких инструментов как фагот, виолончель и тромбон.

Давайте проиллюстрируем:

Заметим, что когда-то ключей «До» было больше. Ключ «До» на 1-й линии назывался сопрановым, на 2-й – меццо-сопрановым, на 5-й – баритоновым, а употреблялись они для вокальных партий соответственно указанным диапазонам. Вообще, разные ключи в нотах нужны, чтобы не делать добавочные линии нотоносца в избыточных количествах и облегчить восприятие нот. К слову, чтобы упростить чтение нот, используется ряд дополнительных обозначений, о которых мы сейчас поговорим.

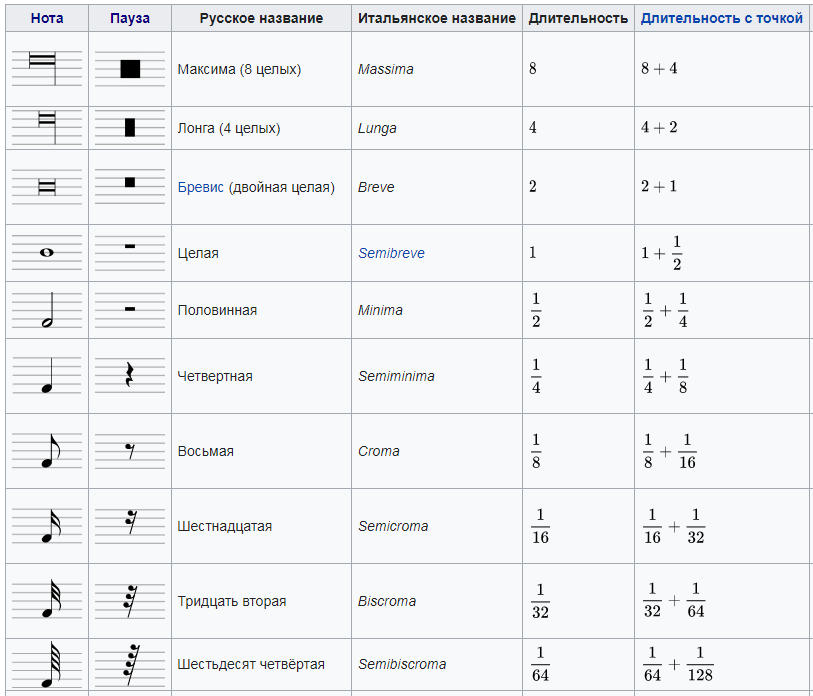
Длительности нот

Когда на 1-м уроке мы изучали физические свойства звука, мы узнали, что для музыкального звука важной характеристикой является его длительность. Глядя на нотный стан, музыкант должен понимать не только то, какую ноту нужно сыграть, но и как долго она должна звучать.

Чтобы было проще ориентироваться, кружочки нот могут быть светлыми или темными (пустыми или заштрихованными), иметь дополнительные «хвостики», «палочки», «линии» и прочее. Глядя на эти нюансы, сразу понятно, целая это нота или половинная, или еще какая-либо. Осталось разобраться, что значит «целая» нота, «половинная» и т.д.

Как считать длительности:

1	Целая нота– тянется на равномерный отсчет «раз и 2 и 3 и 4 и» (звук «и» в конце произносится обязательно – это важно).
2	Половинная– тянется на отсчет «раз и 2 и».
3	Четвертная – тянется на «раз и».
4	Восьмая– тянется на «раз» или на звук «и», если восьмые идут подряд.
5	Шестнадцатая– успевает повториться дважды на слово «раз» или на звук «и».

Понятно, что считать можно с разной скоростью, поэтому для унификации счета используется специальное устройство: метроном. Там четко выверено расстояние между звуками и устройство как бы считает вместо вас. Сейчас существует бесчисленное множество программ с функцией метронома, как самостоятельных, так и имеющих данную опцию в составе других мобильных приложений для музыкантов.

В Google Play можно найти, к примеру, программу-метроном Soundbrenner, а можно скачать программу для настройки гитары Guitar Tuna, где в разделе «Инструменты» будет «Библиотека аккордов» и «Метроном» (не забудьте разрешить приложению доступ к микрофону). Далее давайте разберемся, как обозначается длительность нот.

Длительности (обозначения):

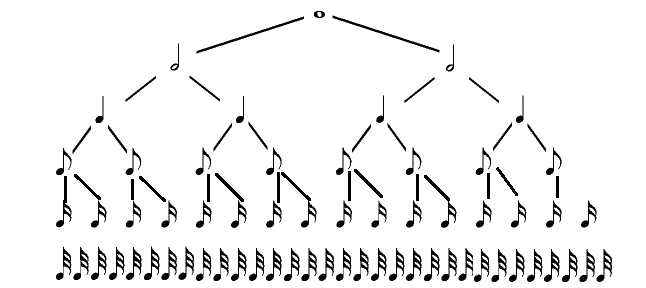
Целая нота – светлый (незакрашенный) значок.
Половинная – светлый (незакрашенный) значок + штиль (вертикальная линия).
Четвертная– темный (заштрихованный) значок + штиль.
Восьмая– темный (заштрихованный) значок + штиль с «флажком» (он же «хвостик»).
Шестнадцатая– темный (заштрихованный) значок + штиль с двойным «хвостиком».
Тридцатьвторая – темный (заштрихованный) значок + штиль с тройным «флажком».
Точки справа от ноты увеличивают долготу звука в 1,5 раза.

Думается, принцип понятен, а для наглядности предлагаем вам следующую иллюстрацию:

Если 8-е, 16-е, 32-е ноты идут подряд, их принято объединять в группы и не «пестрить» большим количеством «хвостиков» или «флажков». Для этого применяется так называемое «ребро». По количеству ребер можно сразу понять, какие именно ноты объединены в группу для проигрыша.

Объединение нот в группу:

1 ребро – восьмые.
2 ребра – шестнадцатые.
3 ребра – тридцать вторые.
4 ребра – шестьдесят четвертые.

Вот как это выглядит:

Обычно ноты объединяются внутри такта. Напомним, что такт – это ноты и сопутствующие им знаки между двумя вертикальными линиями, которые именуются тактовыми чертами:

Как вы заметили, штиль может смотреть наверх либо вниз. Тут есть свои закономерности.

Направление штиля:

Для записи одной мелодической линии без моментов, когда звучат одновременно две ноты или больше, штили направляю вверх для нот, изображенных ниже середины нотного стана, и вниз для нот, нарисованных выше середины нотного стана. Штили нот на 3-й (средней) линии могут быть направлены и вверх, и вниз, но чаще их направляют вниз.
Для записи двух мелодических линий, когда могут звучать несколько нот одновременно, штили для нот «верхней» мелодии смотрят вверх, для «нижней» мелодии – вниз.

Более подробную информацию про длительности нот можно найти у Вахромеева в «Элементарной теории музыки [В. Вахромеев, 1961].

И, наконец, в любой мелодии есть и звуки, и паузы между ними. Поговорим о них.

Паузы

Паузы измеряются по такому же принципу, как нотные длительности. Пауза точно так может быть целой, половинной и т.д. Однако пауза может длиться дольше, чем целая нота, и для таких случаев придуманы особые названия. Так, если пауза длится в 2 раза дольше, чем целая нота, ее называют бревис, если в 4 раза дольше – это лонга, в 8 раз – максима. Полный перечень названий с обозначениями можно увидеть в нижеследующей таблице:

Итак, на сегодняшнем уроке вы познакомились с нотной грамотой «с нуля», получили представление о знаках альтерации, написании нот, обозначении пауз и других связанных с этой темой понятиях. Думаем, что для одного задания этого более чем достаточно. Теперь осталось закрепить ключевые моменты урока с помощью проверочного теста.

Тест на усвоение материала урока

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

А теперь переходим к изучению гармонии в музыке.

Источник

Алгебра что такое ноты

Алгебра гармонии