Чистая квинта от ноты ля бемоль

Из таблицы видно, что тоновая величина чистой квинты – 3,5 тона, чистой кварты – 2,5 тона. С помощью этих интервалов строится кварто-квинтовый круг тональностей.

Мы проверим это в соответствующем разделе статьи.

Объяснение магии кварто-квинтового круга заключается в том, что чистая квинта – это обращение чистой кварты, т.е. если переместить основание чистой квинты на октаву вниз – получится чистая кварта.

Для закрепления информации стоит запомнить аппликатуры этих интервалов на гитаре и фортепиано.

Тональность – это высотное положение лада, построенного от определенной ноты. Другими словами: тональность – это высота звучания музыкального произведения, которая определяется тоникой.

Параллельные тональности – это мажорная и минорная тональность, которые имеют разную тонику, но содержат одинаковый набор нот и ключевых знаков.

Знаки альтерации – это знаки, которые используются при нотном письме и обозначают повышение или понижение высотности звука без изменения его названия. Эта тема частично затрагивалась в статье «Как быстро научиться играть на гитаре с нуля».

# – диез – повышает звук на полутон, b – бемоль – понижает. Также существуют дубль-диезы и дубль-бемоли, которые повышают или понижают звук на целый тон.

Теперь мы знаем всю необходимую теорию, чтобы построить кварто-квинтовый круг тональностей. На картинке видно, что начальной точкой отсчета служит нота До. От неё и будем строить наш круг.

Мы уже знаем, что чистая квинта имеет тоновую величину 3,5 тона. Отложим этот интервал по восходящему звукоряду от ноты До.

Первая чистая квинта по восходящему звукоряду от ноты До привела к ноте Соль. Следующая чистая квинта от ноты Соль – нота Ре. Если продолжить откладывать чистые квинты по восходящему звукоряду – мы снова вернемся к ноте До.

Теперь проделаем то же самое с чистыми квартами.

Первая чистая кварта по восходящему звукоряду от ноты До – нота Фа. Следующая чистая кварта от ноты Фа – нота Си-бемоль. Здесь действует такое же правило. Если мы продолжим последовательно откладывать чистые кварты по восходящему звукоряду – мы вернемся к ноте До.

Для лучшего понимания теории и схемы построения кварто-квинтового круга тональностей – взгляните на ступени по которым он строится на восходящем звукоряде. Для удобства чистые кварты обозначены красным цветом, чистые квинты – синим.

Проверяем эту теорию по нашему квинтовому кругу.

Из всего этого можно сделать вывод о том, как построить кварто-квинтовый круг:

по часовой стрелке – квинтами вверх;
против часовой стрелки – квартами вверх.

Раз чистая квинта – это обращением чистой кварты, то если идти по часовой стрелке квартами вниз или против часовой стрелки квинтами вниз – мы получим совершенно идентичный набор нот.

Самое очевидное применение кварто-квинтового круга – транспозиция. Может возникнуть ситуация, когда вы хотите спеть какую-нибудь лёгкую песню, но её тональность не подходит под ваш голосовой диапазон. В таком случае мы представляем, что наш кварто-квинтовый круг – это довольно понятная схема аккордов и их последовательностей, а не схема тональностей.

Поворачиваем квинтовый круг по часовой стрелке или против – получаем другую тональность. Аккорды изменятся, но их функции сохранятся.

Пробуем петь в новой тональности и радуемся. Если тональность не подошла – снова вращаем наш круг до тех пор, пока не найдём комфортную тональность.

Теперь разберем эти манипуляции на живом примере. Будем делать транспозицию для песни группы Кино «Кукушка».

В оригинале эта песня исполняется в тональности Ля минор. Находим на квинтовом круге эту тональность, внимательно смотрим на то, как расположены аккорды песни на квинтовом круге и поворачиваем его.

Мы транспонировали песню из тональности Ля минор в Ми минор. Осталось попробовать спеть в новой тональности и определить подходит она или нет.

Если не можете запомнить как располагаются аккорды песни на квинтовом круге – можно записать результаты транспонирования в виде таблицы.

В предыдущем разделе статьи мы уже говорили, что можно воспринимать кварто-квинтовый круг не как схему тональностей, а как схему аккордов для гитары.

Это даёт нам возможность не задумываться каждый раз, когда мы хотим сочинить гитарный аккомпанемент к своей песне и не тратить время на бесконечное перебирание базовых аккордов и их последовательностей. Всё что нужно – уже есть в кварто-квинтовом круге тональностей.

Тоника, доминанта и субдоминанта – это основные устойчивые ступени лада и квинтовый круг позволяет сразу найти доминанту и субдоминанту для любой тональности.

Доминанта и субдоминанта создают основное движение в музыкальном произведении.

Доминанта имеет максимальное напряжение и стремится разрешиться в тонику. Субдоминанта уводит нас в противоположную сторону, поэтому субдоминанту часто используют для модуляции.

Если посмотреть на любую тональность на квинтовом круге, то доминанта всегда будет следующей нотой после тоники по часовой стрелке, а субдоминанта – следующей нотой против часовой стрелки.

Например, для тональности До мажор доминантой будет Соль, субдоминантой – Фа.

То же правило справедливо для минорных тональностей, с одной оговоркой – минорный аккорд не может быть полноценной доминантой и следует использовать мажорный аккорд в тех случаях, когда он должен разрешиться в тонику. Таким образом, в тональности Ля минор субдоминантой будет Ре минор, а доминантой Ми мажор.

Давайте рассмотрим несколько тональностей на квинтовом круге и разберемся в этом.

Мы видим, что в тональности До мажор и её параллельной тональности Ля минор самыми логичными и ожидаемыми будут аккорды C, G, F, Am, Dm, Em. К этим аккордам добавится Ми мажор, если речь идет о минорной тональности.

Подавляющее большинство популярной музыки написано по такой схеме, не выходя за рамки тональности в квинтовом круге. Именно эти аккорды стоит использовать в первую очередь при написании гитарного аккомпанемента.

Если такой подход кажется вам скучным и вы хотите как-то разнообразить аккомпанемент – можете позаимствовать аккорды из соседних тональностей.

Источник

Кварто-квинтовый круг тональностей

Кварто-квинтовый круг тональностей или просто квинтовый круг – это схема для удобного и быстрого запоминания всех тональностей и ключевых знаков в них.

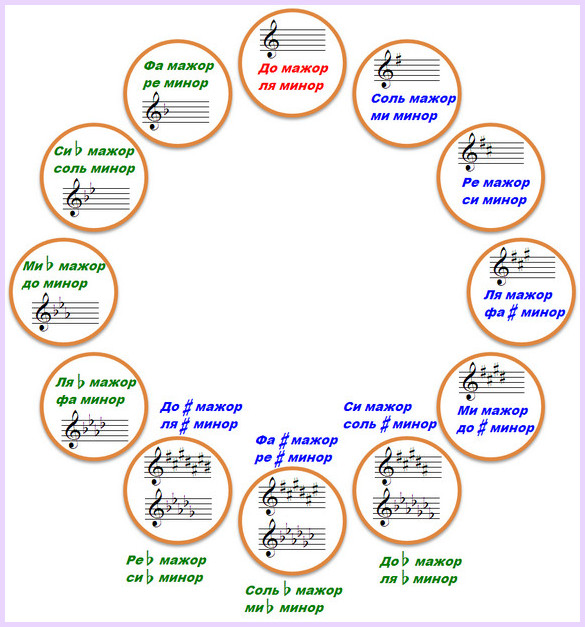
В вершине квинтового круга находится тональность До мажор; по часовой стрелке – диезные тональности, тоники которых расположены по чистым квинтам вверх от тоники исходного До мажора; против часовой стрелки – круг бемольных тональностей, расположенных также по чистым квинтам, но только вниз.

При этом, при движении по квинтовому круг по часовой стрелке с каждой новой тональностью постепенно возрастает количество диезов (от одного до семи), при движении против часовой стрелки, соответственно, от одной тональности к другой возрастает количество бемолей (также от одного до семи).

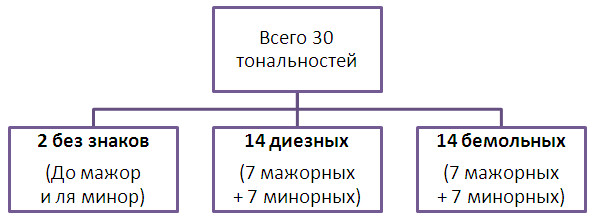
Сколько всего в музыке тональностей?

В музыке применяется, главным образом, 30 тональностей, из которых одна половина – мажорные, а другая – минорные. Мажорные и минорные тональности образуют пары по принципу совпадения в них ключевых знаков альтерации – диезов и бемолей. Тональности с одинаковыми знаками называются параллельными. Всего, таким образом, есть 15 пар параллельных тональностей.

Из 30 тональностей две не имеют знаков – это До мажор и ля минор. 14 тональностей имеют диезы (от одного до семи по порядку диезов ФА ДО СОЛЬ РЕ ЛЯ МИ СИ), из этих 14 семь тональностей будут мажорные, а семь, соответственно, минорные. Ещё 14 тональностей имеют бемоли (аналогично от одного до семи, но только по порядку бемолей СИ МИ ЛЯ РЕ СОЛЬ ДО ФА), из них также семь мажорных и семь минорных.

Таблицу всех используемых музыкантами в практике тональностей вместе с их знаками можно скачать ЗДЕСЬ, распечатать и пользоваться ей как шпаргалкой.

Объяснение: как образуется квинтовый круг?

Квинта в этой схеме – самый главный интервал. Почему именно чистая квинта? Потому что квинта – это физически (акустически) наиболее естественный способ перехода от одного звука к другому, и этот простой интервал был рождён самой природой.

Итак, диезные тональности располагаются по чистым квинтам вверх. Первая квинта строится от ноты «до», то есть от тоники До мажора, чистой тональности без знаков. Квинта от «до» — это «до-соль». Значит, нота «соль» становится тоникой следующей тональности по квинтовому кругу, это будет тональность Соль мажор и в ней будет один знак – фа-диез.

Следующую квинту строим уже от звука «соль» — «соль-ре», полученный звук «ре» — тоника очередной тональности квинтового круга – тоника гаммы Ре мажор, в которой два знака – два диеза (фа и до). С каждой построенной квинтой мы будем получать новые диезные тональности, и количество диезов будет все более возрастать, пока не достигнет семи (пока все ступени не окажутся повышенными).

Таким образом, если строить квинты, начиная от «до», то у нас получается следующий ряд тональностей: Соль мажор (1 диез), Ре мажор (2 диеза), Ля мажор (3 диеза), Ми мажор (4 диеза), Си мажор (5 диезов), Фа-диез мажор (6 диезов), До-диез мажор (7 диезов). Ряд записанных тоник оказался настолько широк своим размахом, что приходится начинать записывать его в басовом ключе, а заканчивать в скрипичном.

Порядок, в котором прибавляются диезы: ФА, ДО, СОЛЬ, РЕ, ЛЯ, МИ, СИ. Диезы также отстоят друг от друга на интервал чистой квинты. Это связано вот с чем. Каждый новый диез появляется на седьмой ступени гаммы, об этом мы говорили ещё в статье «Как запомнить знаки в тональностях». Соответственно, если тоники новых тональностей всё время отодвигаются на чистую квинту, то и их седьмые ступени также отодвигаются друг от друга ровно на чистую квинту.

Бемольные мажорные тональности располагаются по чистым квинтам вниз от «до». Точно также с каждой новой тональностью происходит увеличение количества бемолей в гамме. Ряд бемольных тональностей следующий: Фа мажор (один бемоль), Си-бемоль мажор (2 бемоля), Ми-бемоль мажор (3 бемоля), Ля-бемоль мажор (4 бемоля), Ре-бемоль мажор (5 бемолей), Соль-бемоль мажор (6 бемолей) и До-бемоль мажор (7 бемолей).

Порядок появления бемолей: СИ, МИ, ЛЯ, РЕ, СОЛЬ, ДО, ФА. Бемоли так же, как и диезы, добавляются по квинтам, только вниз. Более того, порядок бемолей совпадает с порядком тональностей бемольной ветви кварто-квинтового круга, начиная с Си-бемоль мажора.

Ну а теперь, наконец, представим собственно весь круг тональностей, в который для полноты отображения мы добавим ещё и параллельные миноры для всех мажоров.

Кстати, квинтовый круг нельзя строго назвать кругом, он представляет собой скорее некое подобие спирали, так как на определённом этапе некоторые тональности пересекаются из-за совпадения по высоте звучания. Кроме того, квинтовый круг не является замкнутым, его можно продолжить новыми более сложными тональностями с двойными знаками альтерации – дубль-диезами и дубль-бемолями (такие тональности используются в музыке крайне редко). О совпадающих по звучанию тональностях мы ещё поговорим отдельно, но чуть позже.

Откуда взялось название «кварто-квинтовый круг»?

До сих пор мы рассматривали движение в круге только по квинтам и ни разу не упоминали кварты. Так при чём же тут они? Почему полное название схемы звучит именно как «кварто-квинтовый круг»?

Дело в том, что кварта является обращением интервала квинты. И тот же ряд тональностей круга можно получить если двигаться не по квинтам, а по квартам.

Например, диезные тональности можно расположить не по чистым квинтам вверх, а по чистым квартам вниз. Получится тот же самый ряд:

Бемольные тональности можно расположить не по чистым квинтам вниз, а по чистым квартам вверх. И снова результат будет один и тот же:

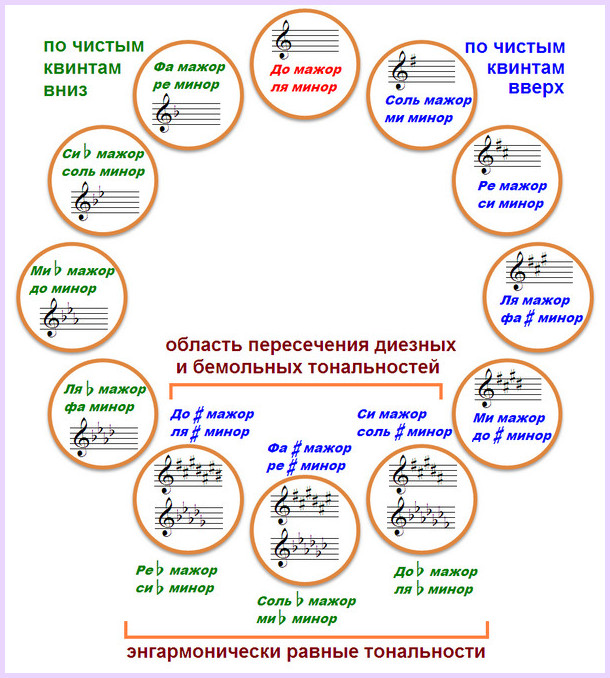
Энгармонически равные тональности

Энгармонизм в музыке – это совпадение элементов по звучанию, но разность их по названию, написанию или обозначению. Энгармонически равными могут быть простые ноты: например, до-диез и ре-бемоль. Энгармонизм характерен и для интервалов или аккордов. А в данном случае мы будем иметь дело с энгармонически равными тональностями , соответственно, звукоряды гамм этих тональностей также будут совпадать по звучанию.

Как мы уже отметили, такие совпадающие по звучанию тональности появляются на пересечении диезной и бемольной ветвей квинтового круга. Это тональности с большим числом знаков – с пятью, шестью или семью диезами или бемолями.

К энгармонически равным относят следующие тональности:

Си мажор (5 диезов) и До-бемоль мажор (7 бемолей)
Параллельные названным соль-диез минор (5 диезов) и ля-бемоль минор (7 бемолей);
Фа-диез мажор (6 диезов) и Соль-бемоль мажор (6 бемолей);
Параллельные им ре-диез минор и ми-бемоль минор с таким же количеством знаков;
До-диез мажор (7 диезов) и Ре-бемоль мажор (5 бемолей);
Параллельные этим строям ля-диез минор (тоже 7 диезов) и си-бемоль минор (5 бемолей).

Как пользоваться квинтовым кругом тональностей?

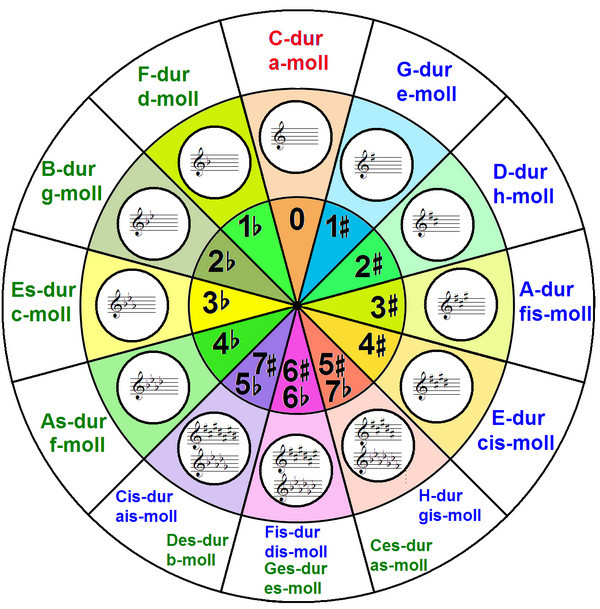
Во-первых, квинтовым кругом можно пользоваться как удобной шпаргалкой для выучивания всех тональностей и их знаков.

Во-вторых, по квинтовому кругу можно легко определить разницу в знаках между двумя тональностями. Для этого достаточно просто посчитать сектора от исходной тональности до той, с которой мы сравниваем.

Например, между Соль мажором и Ми-мажором разница в три сектора, и, значит, в три знака. Между До мажором и Ля-бемоль мажором разница в 4 бемоля.

Разницу в знаках нагляднее всего показывает квинтовый круг, поделённый на сектора. Для того чтобы изображение круга было компактным, тональности в нём можно записывать с помощью буквенного обозначения:

Наконец, в-третьих, по квинтовому кругу мгновенно можно установить «ближайших родственников» той или иной тональности, то есть определить тональности первой степени родства. Они находятся в том же секторе, что и исходная тональность (параллельная) и в соседних с каждой стороны.

Например, для Соль мажора такими родственными тональностями будут считаться ми минор (в том же секторе), а также До мажор и ля минор (соседний сектор слева), Ре мажор и си минор (соседний сектор справа).

К более подробному изучению родственных тональностей мы ещё вернёмся в будущем, тогда и узнаем все способы и секреты их розыска.

Немного об истории квинтового круга

Никто точно не знает, когда и кем был изобретён кварто-квинтовый круг. Но ранние описания похожей системы содержатся ещё в рукописи далёкого 1679 года – в труде «Мусикийская грамматика» Николая Дилецкого. Его книга предназначалась для обучения церковных певчих. Круг мажорных строёв он именует «колесом весёлой мусикии», а круг минорных – колесом «мусикии печальной». Мусикия – это слово переводится как «музыка» со славянского.

Сейчас, конечно, этот труд представляет интерес, главным образом, как исторический и культурный памятник, сам по себе теоретический трактат уже не отвечает требованиям современности. Однако можно сказать, что с тех пор, квинтовый круг закрепился в практике обучения и вошёл почти во все известные отечественные учебники по теории музыки.

Дорогие друзья! Если вопросы по теме квинтового круга ещё себя не исчерпали, то обязательно напишите их в комментариях к данной статье. На прощание предлагаем вам послушать немного хорошей музыки. Пусть сегодня это будет знаменитый романс Михаила Ивановича Глинки «Жаворонок» (стихи поэта Николая Кукольника). Певица — Виктория Иванова.

Думал никогда не разберусь, но когда так наглядно и четко объясняют, грех не понять 🙂 Спасибо !

Спасибо! Наконец-то я понял, буду закреплять на практике

Огромное вам спасибо! Думал уже двойка за урок будет… Спасибочки авторам этой страницы!

Здравствуйте, а можете пожалуйста объяснить зачем вообще нужен этот круг? То есть как нам помогает знание того, сколько в какой гамме бемолей и диезом? Ведь мне нужно построить гамму Соль мажор, к примеру. Я смотрю на круг, вижу, что будет 1 диез. Далее, можно определить что диез будет для ноты Фа. Но ведь этих данных недостаточно для построения гаммы. Приходится все равно пользоваться правилом «тон-тон-полутон-….». Так что нам дает это знание?
Или я в что-то конкретно не врубаюсь?

Никита, суть как раз и заключается в том, чтобы не считать тона и полутона каждый раз для получения верной гаммы, а знать конкретно и сразу, какие звуки будут понижены или повышены в данной гамме. Соль мажор — 1 диез, значит играем от СОЛЬ до СОЛЬ через фа-диез; Ре мажор — 2 диеза, значит, играем от РЕ до РЕ все ноты подряд, только фа и до будут повышены (диезами); Ля мажор — 3 диеза, значит, играем от ЛЯ до ЛЯ подряд все ноты, только фа, до и соль будут с диезами и т.д.

А вообще квинтовый круг нужен не только для определения знаков в тональностях, но и для других целей: например, для быстрого нахождения родственных тональностей (у каждой тональности по 6 родственников), для понимания, как можно перейти из одной тональности в другую (это называется модуляция) и др.

Знаки в тональностях можно также определять по-другому, читайте подробнее об этом здесь — https://muz-teoretik.ru/kak-zapomnit-znaki-v-tonalnostyax/

Со временем, после недолгой практики путешествия по разным тональностям, их знаки (диезы и бемоли) запомнятся сами собой. Необходимость что-то считать отпадёт. Любой образованный музыкант ничего не вычисляет, он просто знает (как 2+2), сколько диезов или бемолей и какие именно есть в той или иной тональности.

Спасибо большое за столь оперативный ответ!
Я все понял

Ничего непонятно. Объяснять не можешь. Это тупая, сухая теория — никому неинтересна. Где примеры, доказательства? Чистый, тупой груз: на тему разберись сам.

Яша, кажется что тупой здесь кое-кто другой, а не теория.

Что ж поделать? Попробуйте разобраться ещё раз или поищите другое объяснение, может быть, действительно, какой-нибудь другой подход к проблеме поможет.

Здравствуйте.Никак не могу получить больше 6и диезов\бемолей. 1,2,3,4,5,6 совпадает. а вместо 7и опять 6 получается.
Пример: Cis-dur= c#, d#, f, f#, g#, a#, c,c#. где еще 7й взяли?

В До мажоре знаков нет, в До-диез мажоре все ступени повышены: до-диез, ре-диез, ми-диез, фа-диез, соль-диез, ля-диез, си-диез.

Ми диез и Си диез ? =). Нет же таких нот.

Очень интересная статья, а главное разжеванное самим автором!
Спасибо большое за многочасовые усилия, для чайников самое то.
Только вот предусмотрен ли этот круг для всех инструментов?
К примеру я басист, в моем случае здесь понимание этой схемы предоставит шансы к легкому запоминанию и перебиранию модуляции и гамм?

Все ясно и понятно ! Все вы строилось в четкую картину . Спасибо автору . Сама все поняла и внучке семилетней объяснила , она тоже все поняла . Теперь тренируемая , чтоб от » зубов » отлетало

Спасибо за статью. Только начинаю разбираться. Ещё вот нашел подробную статью о том, как пользоваться квинтовым кругом. Если кому-то вдруг будет интересно углубиться https://guitar-geek.ru/lessons/kvarto-kvintovyj-krug

Сегодня с утра мне подумалось. Вот пришло в голову Пифагору поделить струну на 3 части и услышал он квинту от главного звука. Вот решил он поэкспериментировать — попробовать делить полученный звук снова на треть и так далее. И получил он настоящий музыкальный строй, который назвали его именем.

Квартово-квинтовый круг, кстати, является как бы иллюстрацией метода Пифагора по нахождению нот. Но у Пифагора в его методе получилась погрешность (или особенность) — октава не сошлась, и это расхождение назвали пифагоровой коммой. Если бы квартово-квинтовый круг отражал бы пифагоров строй, то у нас в круге возникли бы две ноты фа слегка отличающиеся друг от друга.

С проблемой комм бились полторы тыщи лет пока не придумали равномерно-темперированный строй. И тут, с утра, подумалось мне, а если бы Пифагор решил делить струну не квинтой, а терцией, как тогда бы шёл его опыт?

Для начала я взял большую терцию (соотношение частот 5/4), калькулятор и начал шагать методом Пифагора: каждый полученный результат снова умножать на 5/4 и загонять в октаву делением, кратным двум. Но у меня стало получаться очень много ступеней. Судить, насколько они приятны на слух и полезны для создания музыки, я не стал. Тут мне пришлось бы повозиться: включить программу «генератор частот», записать в аудиоредактор эти частоты, поиграться с ними. Причём, я заранее знаю, что вряд ли приму их за полезную находку. Ведь мой слух привык к равномерной темперации, и даже древний пифагоров строй может показаться не совсем правильным, а тем более всякие многоступенные строи, типа индийских. То есть, я подумал, что овчинка не стоит выделки.

Затем я подумал, какими ещё интервалами можно было бы поделить основной тон для получения нот? И я обратил внимание на кварту. Кварта — это как бы изнанка квинты — квинта в другую сторону. Может быть результат у меня получится идентичным квинтовому делению? Я начал делить калькулятором, получая, порою, по пять знаков после запятой. Возможно, что это вносило свою погрешность. Но пока я пришёл к выводу, что если бы Пифагор делил тон не на 2/3 (квинта), а на 4/5 (кварта), то он получил бы слегка другие ноты и комму, конечно тоже получил бы.

Так устроено природой, что есть во всех этих соотношениях есть что-то подобное бесконечному иррациональному числу пи, и нам, чтобы как-то жить, приходится что-то округлять, подгонять. Таким образом, даже чистая квинта в равномерной темперации не чиста — её «округлили» ради других интервалов. И тогда я подумал — а если попробовать делить тон темперированной квинтой, то всё ли сойдётся с нашими привычными нотами? 😊

Наверное, 30 тональностей, это чисто теоретически. На практике, слушая музыку и определяя её тональность (допустим, с помощью инструмента) для нас ведь равнозначны до-диез или ре-бемоль. Это автор мог постановить что данное произведение написанов до-диез, к примеру, а для слушателя до-диез и ре-бемоль это одно и то же ведь? И тогда, получается, что квартово-квинтовый круг описывает 16 тональностей (7 минорных альтерированных, 7 мажорных альтерированных и 2 без знаков альтерации). Так?

Нет, увы. Если одинаковые по звучанию, но разные по обозначению тональности считать за одну и ту же (всего 6 пар таких тональностей), то от 30 останется 24 (12 мажорных и 12 минорных). В принципе, я бы голосовал за то, чтобы упразднить такие ненужные обозначения нот, как ми-диез (нота фа), си-диез (нота до) и, соответственно, фа-бемоль, до-бемоль. Но, тут, как в математике. Теория предписывает их использование и от этого никуда не деться.

Источник