Что такое резонанс гитары

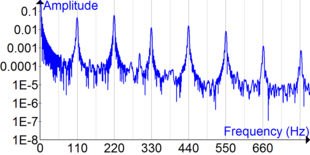
Звуковой резонанс и интерференция звука

Каждый, кто мало-мальски профессионально играет на акустической гитаре или скрипке, знает, как важен материал, из которого изготовлен инструмент, и его окраска. И важно это совсем не для того, чтобы инструмент выглядел красиво, а для правильного звукоизвлечения. Почему же так важен корпус? Как он влияет на свойства звука?

Резонанс звуковых волн

Чтобы ответить на этот вопрос надо вспомнить, что такое явление резонанса. Когда колебания какой-либо колебательной системы совпадают с вынуждающими колебаниями, происходит их резкое усиление. В этом заключается явление резонанса. А так как звук это тоже колебания, то логично предположить, что явление резонанса не чуждо и звуку. И это так.

Например, если расположить рядом два камертона и легонько стукнуть по одному из них, то приглушив его, можно услышать, как издает звук и другой, которого не касались. Это происходит вследствие того, что второй камертон попадает в резонанс с первым и его колебания резко возрастают. Так осуществляется звуковой резонанс.

Звуковой резонанс в гитаре

Вернемся к гитаре. Звук, издаваемый самой гитарной струной не слишком громкий. Для того, чтобы усилить этот звук, струны располагают поверх корпуса, который делают специальной формы и размера. В середине корпуса обязательно имеется отверстие круглой формы для выхода звука. Звук струны, попадая внутрь корпуса, резонирует и усиливается, отчего гитара звучит намного громче.

Настройка гитары — это также пример явления звукового резонанса. Если настроить первую струну по камертону, а потом зажать вторую струну на определенном ладу (опредлеленная нота) и дернуть ее, то можно увидеть, как первая струна слегка поддергивается (при условии, что гитара настроена правильно).

От качества дерева, из которого изготовлена гитара, зависит не только сила, но и чистота, и тембр извлекаемого звука. Влияет на это и покраска, и лак на дереве. Именно поэтому изготовить качественную гитару или скрипку совсем не просто, и качественные инструменты стоят больших денег. Так, явление звукового резонанса из физики перекочевало в иные сферы и плотно там обосновалось.

Интерференция звука

Звук, как и любые другие колебания, может не только резонировать, но и создавать более сложные картины. Например, в случае, когда мы имеем звуковые колебания одной частоты и разности фаз, будет происходить интерференция звука.

Колебания будут складываться, и суммарная звуковая волна будет зависеть от того, как расположены по отношению друг к другу волновые фазы. В точках, где фазы волн будут одинаковы, их амплитуда будет максимальна, а в противофазе их амплитуда будет равна нулю.

То есть будут места, где звук будет очень громким, а в некоторых местах будет стоять тишина, несмотря на прохождение через это место звуковых волн. Но это можно наблюдать в основном в лаборатории, так как в жизни практически не приходится встречать подобные ситуации, когда мы имеем звуковые волны одинаковых частот и разности фаз без присутствия посторонних звуков.

Источник

Акустический резонанс — Acoustic resonance

Акустический резонанс — это явление, при котором акустическая система усиливает звуковые волны, частота которых совпадает с одной из ее собственных частот вибрации (ее резонансными частотами ).

Термин «акустический резонанс» иногда используется для сужения механического резонанса до частотного диапазона человеческого слуха, но поскольку акустика определяется в общих терминах, касающихся колебательных волн в веществе, акустический резонанс может возникать на частотах за пределами диапазона человеческого слуха.

Акустически резонансный объект обычно имеет более одной резонансной частоты, особенно на гармониках самого сильного резонанса. Он будет легко вибрировать на этих частотах и ​​менее сильно вибрировать на других частотах. Он будет «выделять» свою резонансную частоту из сложного возбуждения, такого как импульсное или широкополосное шумовое возбуждение. Фактически, он отфильтровывает все частоты, кроме резонанса.

Акустический резонанс — важное соображение для производителей инструментов, поскольку в большинстве акустических инструментов используются резонаторы , такие как струны и корпус скрипки , длина трубки в флейте и форма мембраны барабана. Акустический резонанс также важен для слуха. Так , например, резонанс структурного элемента жесткого, называемый базилярная мембрана в улитке части внутреннего уха позволяет волосковые клетки на мембране , чтобы обнаружить звук. (У млекопитающих мембрана имеет сужающиеся резонансы по всей длине, так что высокие частоты сосредоточены на одном конце, а низкие — на другом.)

Как и механический резонанс, акустический резонанс может привести к катастрофическому отказу вибратора. Классический пример этого — разбивание бокала звуком с точной резонансной частотой бокала.

СОДЕРЖАНИЕ

Вибрирующая струна

В музыкальных инструментах натянутые струны, такие как лютни , арфы , гитары , пианино , скрипки и т. Д., Имеют резонансные частоты, напрямую связанные с массой, длиной и натяжением струны. Длина волны, которая создаст первый резонанс на струне, равна удвоенной длине струны. Более высокие резонансы соответствуют длинам волн, которые являются целыми делениями основной длины волны. Соответствующие частоты связаны со скоростью V в виде волны , распространяющейся вдоль струны по уравнению

ж знак равно п v 2 L <\ displaystyle f = >

где L — длина струны (для струны, закрепленной на обоих концах) и n = 1, 2, 3 . ( гармоника в трубе с открытым концом (то есть оба конца трубы открыты)). Скорость волны через струну или проволоку связана с ее натяжением T и массой на единицу длины ρ:

v знак равно Т ρ <\ displaystyle v = <\ sqrt >>

Таким образом, частота связана со свойствами струны уравнением

ж знак равно п Т ρ 2 L знак равно п Т м / L 2 L <\ displaystyle f = > \ over 2L> = > \ over 2L>>

где T — натяжение , ρ — масса на единицу длины, m — общая масса .

Более высокое натяжение и меньшая длина увеличивают резонансные частоты. Когда струна возбуждается импульсной функцией (выщипывание пальцем или удар молотком), струна колеблется на всех частотах, присутствующих в импульсе (импульсная функция теоретически содержит «все» частоты). Те частоты, которые не являются одним из резонансов, быстро отфильтровываются — они ослабляются — и все, что остается, — это гармонические колебания, которые мы слышим как музыкальную ноту.

Струнный резонанс в музыкальных инструментах

Струнный резонанс возникает на струнных инструментах . Струны или части струн могут резонировать на своих основных частотах или частотах обертона, когда звучат другие струны. Например, струна A на 440 Гц вызовет резонанс струны E на 330 Гц, потому что они имеют общий обертон 1320 Гц (3-й обертон A и 4-й обертон E).

Резонанс трубки воздуха

Резонанс трубки с воздухом зависит от длины трубки, ее формы и того, имеет ли она закрытые или открытые концы. Многие музыкальные инструменты напоминают трубы конической или цилиндрической формы (см. Отверстие ). Труба, которая закрыта с одного конца и открыта с другого, называется остановленной или закрытой, в то время как открытая труба открыта с обоих концов. Современные оркестровые флейты ведут себя как открытые цилиндрические трубы; кларнеты ведут себя как закрытые цилиндрические трубы; и саксофоны , гобои и фаготы в виде закрытых конических труб, в то время как большинство современных инструментов с язычком для губ ( медные духовые инструменты ) акустически похожи на закрытые конические трубы с некоторыми отклонениями (см. тембры педалей и ложные звуки ). Как и струны, колеблющиеся воздушные колонны в идеальных цилиндрических или конических трубах также имеют резонансы на гармониках, хотя есть некоторые отличия.

Цилиндров

Любой цилиндр резонирует на нескольких частотах, создавая несколько музыкальных нот. Самая низкая частота называется основной частотой или первой гармоникой. Цилиндры, используемые в качестве музыкальных инструментов, обычно открыты либо с обоих концов, как флейта, либо с одного конца, как некоторые органные трубы. Однако цилиндр, закрытый с обоих концов, также может использоваться для создания или визуализации звуковых волн, как в трубке Рубенса .

Резонансные свойства цилиндра можно понять, рассмотрев поведение звуковой волны в воздухе. Звук распространяется как продольная волна сжатия, заставляя молекулы воздуха двигаться вперед и назад вдоль направления движения. Внутри трубки образуется стоячая волна, длина которой зависит от длины трубки. В закрытом конце трубки молекулы воздуха не могут сильно двигаться, поэтому этот конец трубки является узлом смещения в стоячей волне. На открытом конце трубки молекулы воздуха могут свободно перемещаться, создавая пучность смещения . Узлы смещения являются пучностями давления и наоборот.

Закрыто с обоих концов

В таблице ниже показаны волны смещения в цилиндре, замкнутом с обоих концов. Обратите внимание, что молекулы воздуха около закрытых концов не могут двигаться, тогда как молекулы около центра трубы перемещаются свободно. В первой гармонике замкнутая трубка содержит ровно половину стоячей волны ( узел- пучность- узел).

Частота	Приказ	Имя 1	Название 2	Название 3	Волновое представление	Молекулярное представление
1 · f = 440 Гц	п = 1	1-й частичный	основной тон	1-я гармоника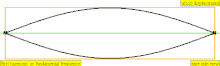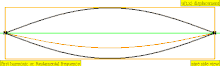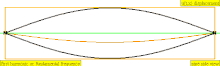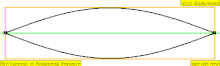
2 · f = 880 Гц	п = 2	2-й частичный	1-й обертон	2-я гармоника
3 · f = 1320 Гц	п = 3	3-й частичный	2-й обертон	3-я гармоника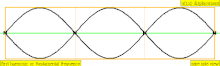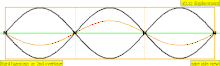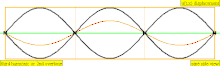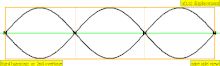
4 · f = 1760 Гц	п = 4	4-я часть	3-й обертон	4-я гармоника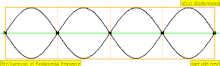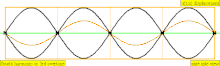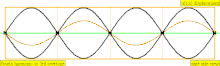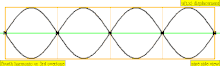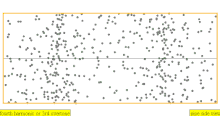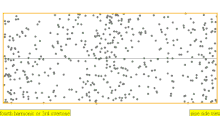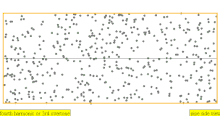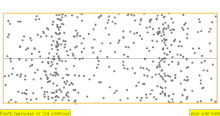

Открыты с обоих концов

В цилиндрах с открытыми обоими концами молекулы воздуха около конца свободно перемещаются в трубу и выходят из нее. Это движение вызывает пучности смещения в стоячей волне. Узлы имеют тенденцию формироваться внутри цилиндра, вдали от концов. В первой гармонике открытая трубка содержит ровно половину стоячей волны (пучность-узел-пучность). Таким образом, гармоники открытого цилиндра рассчитываются так же, как гармоники закрытого / закрытого цилиндра.

Физика трубы, открытой с обоих концов, объясняется в классе физики . Обратите внимание, что на схемах в этом справочнике показаны волны смещения, аналогичные показанным выше. Они резко контрастируют с волнами давления, показанными в конце данной статьи.

По overblowing открытой трубы, примечание может быть получено , что на октаве выше основной частоты или примечания трубки. Например, если основная нота открытой трубы — это C1, то при выдувании трубы за пределы трубы получается C2, которая на октаву выше C1.

Открытые цилиндрические трубки резонируют примерно на частотах:

ж знак равно п v 2 L <\ displaystyle f = >

где n — положительное целое число (1, 2, 3 . ), представляющее резонансный узел, L — длина трубки, а v — скорость звука в воздухе (которая составляет приблизительно 343 метра в секунду [770 миль в час] при 20 ° C [68 ° F]).

Более точное уравнение, учитывающее конечную поправку , приведено ниже:

ж знак равно п v 2 ( L + 0,8 d ) <\ displaystyle f = >

где d — диаметр резонансной трубки. Это уравнение компенсирует тот факт, что точная точка, в которой звуковая волна отражается от открытого конца, находится не идеально в концевой части трубки, а на небольшом расстоянии от нее.

Коэффициент отражения немного меньше 1; открытый конец не ведет себя как бесконечно малый акустический импеданс ; скорее, он имеет конечное значение, называемое импедансом излучения, которое зависит от диаметра трубки, длины волны и типа отражающей панели, которая может присутствовать вокруг отверстия трубки.

Итак, когда n равно 1:

ж знак равно v 2 ( L + 0,8 d ) <\ displaystyle f = > ж ( 2 ( L + 0,8 d ) ) знак равно v <\ Displaystyle <е (2 (L + 0.8d))>= v> ж λ знак равно v <\ displaystyle = v> λ знак равно 2 ( L + 0,8 d ) <\ displaystyle \ lambda = <2 (l + 0.8d)>>

где v — скорость звука, L — длина резонансной трубки, d — диаметр трубки, f — резонансная частота звука, а λ — резонансная длина волны.

Закрыто с одного конца

При использовании в органе труба, которая закрыта с одного конца, называется «закрытой трубой». Такие цилиндры имеют основную частоту, но их можно раздувать для воспроизведения других более высоких частот или нот. Эти раздутые регистры можно настраивать, используя различные степени конической конусности. Закрытая трубка резонирует на той же основной частоте, что и открытая трубка, вдвое превышающая ее длину, с длиной волны, равной четырехкратной ее длине. В закрытой трубе узел смещения или точка отсутствия вибрации всегда появляется на закрытом конце, и если труба резонирует, у нее будет пучность или точка наибольшей вибрации в точке Phi (длина × 0,618) рядом с открытым. конец.

По overblowing цилиндрической закрытой трубки, примечание может быть получено , что приблизительно двенадцатая выше основной ноты трубы, или пятой над октавой фундаментальной ноты. Например, если основной нотой закрытой трубы является C1, то при переполнении трубы получается G2, что на одну двенадцатую выше C1. В качестве альтернативы мы можем сказать, что G2 на одну пятую выше C2 — октавы выше C1. Регулировка конуса этого цилиндра для уменьшения конуса может настроить вторую гармонику или усиленную ноту близко к октавной позиции или 8-й. Открытие небольшого «отверстия динамика» в точке Phi или в общем положении «волна / узел» отменит основную частоту и заставит трубку резонировать на 12-й ступени выше основной. Этот метод используется в записывающем устройстве путем защемления заднего отверстия для большого пальца. Перемещение этого маленького отверстия вверх, ближе к вокалу, сделает его «эхо-дырой» (модификация записывающего устройства Dolmetsch), которая при открытии даст точную половинную ноту выше основной. Примечание. Для точной настройки частоты половинной ноты требуется небольшая регулировка размера или диаметра.

Закрытая трубка будет иметь приблизительные резонансы:

ж знак равно п v 4 L <\ displaystyle f = >

где «n» — нечетное число (1, 3, 5 . ). Этот тип лампы производит только нечетные гармоники, а его основная частота на октаву ниже, чем у открытого цилиндра (то есть вдвое ниже).

Более точное уравнение приведено ниже:

ж знак равно п v 4 ( L + 0,4 d ) <\ displaystyle f = > .

Опять же, когда n равно 1:

ж знак равно v 4 ( L + 0,4 d ) <\ displaystyle f = > ж ( 4 ( L + 0,4 d ) ) знак равно v <\ Displaystyle <е (4 (L + 0,4d))>= v> ж λ знак равно v <\ displaystyle = v> λ знак равно 4 ( L + 0,4 d ) <\ displaystyle \ lambda = <4 (l + 0,4d)>>

где v — скорость звука, L — длина резонансной трубки, d — диаметр трубки, f — резонансная частота звука, а λ — резонансная длина волны.

Волна давления

На двух диаграммах ниже показаны первые три резонанса волны давления в цилиндрической трубе с пучностями на закрытом конце трубы. На схеме 1 трубка открыта с обоих концов. На диаграмме 2 он закрыт с одного конца. Горизонтальная ось — давление. Обратите внимание, что в этом случае открытый конец трубы является узлом давления, а закрытый конец — пучностью давления.

Источник