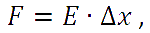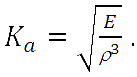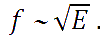Гитара резонирует это как
Сообщений: 5
Регистрация: 10.11.2011

Друзья! У меня обычная классическая гитара Santos Martinez SM50. И я столкнулся с такой проблемой: струны (замечено за басовыми — 4, 5, 6) «заводятся» и звучат, когда их об этом не просят 🙂
Например: я играю какую-нибудь фразу на первых двух струнах (для верности использую апояндо). Басовые струны даже и не трогаю — и все равно они начинают ни с того ни с сего входить в резонанс и издавать гул! Если, к примеру, большой палец лежит на одной из них (соответственно, глушит) — все равно «заводятся» две остальные.
Иногда из-за этого получается жуткий диссонанс, и играть трудно. А уж если с этими шумами «приварить» туда какой-нибудь пьезодатчик и подключить к динамику — даже боюсь представить, что будет.
Поэтому хочется спросить вашего совета — что делать? А именно:
1. Это гитара такая?
2. Это струны такие?
3. Это я такой чайник? 🙂 и так и должно быть?
Вы скажете: «не нравится — глуши пальцами». Согласен. Но, во-первых, в некоторых фрагментах глушить — пальцев не напасешься ни на одной, ни на второй руке.
А во-вторых, вот по этой ссылке
http://www.youtube.com/watch?v=LjMk1mK3O9A — запись вариации на тему «цыганочки» в исполнении гитарного дуэта. На 1:40 дама играет соло с обычной опорой на 6-ю струну, и совершенно понятно, что ее инструмент звучит чисто, «непрошенных» звуков нет. А у меня — есть.
Есть вариант — взять заглушку для гитары, типа вот такой
http://musicsales.ru/show999006677
Но поможет ли она?
Как быть? Вариант «менять гитару» не предлагать. Спасибо всем, кто откликнется!
Источник
Звуковой резонанс и интерференция звука
Каждый, кто мало-мальски профессионально играет на акустической гитаре или скрипке, знает, как важен материал, из которого изготовлен инструмент, и его окраска. И важно это совсем не для того, чтобы инструмент выглядел красиво, а для правильного звукоизвлечения. Почему же так важен корпус? Как он влияет на свойства звука?
Резонанс звуковых волн
Чтобы ответить на этот вопрос надо вспомнить, что такое явление резонанса. Когда колебания какой-либо колебательной системы совпадают с вынуждающими колебаниями, происходит их резкое усиление. В этом заключается явление резонанса. А так как звук это тоже колебания, то логично предположить, что явление резонанса не чуждо и звуку. И это так.
Например, если расположить рядом два камертона и легонько стукнуть по одному из них, то приглушив его, можно услышать, как издает звук и другой, которого не касались. Это происходит вследствие того, что второй камертон попадает в резонанс с первым и его колебания резко возрастают. Так осуществляется звуковой резонанс.
Звуковой резонанс в гитаре
Вернемся к гитаре. Звук, издаваемый самой гитарной струной не слишком громкий. Для того, чтобы усилить этот звук, струны располагают поверх корпуса, который делают специальной формы и размера. В середине корпуса обязательно имеется отверстие круглой формы для выхода звука. Звук струны, попадая внутрь корпуса, резонирует и усиливается, отчего гитара звучит намного громче.
Настройка гитары — это также пример явления звукового резонанса. Если настроить первую струну по камертону, а потом зажать вторую струну на определенном ладу (опредлеленная нота) и дернуть ее, то можно увидеть, как первая струна слегка поддергивается (при условии, что гитара настроена правильно).
От качества дерева, из которого изготовлена гитара, зависит не только сила, но и чистота, и тембр извлекаемого звука. Влияет на это и покраска, и лак на дереве. Именно поэтому изготовить качественную гитару или скрипку совсем не просто, и качественные инструменты стоят больших денег. Так, явление звукового резонанса из физики перекочевало в иные сферы и плотно там обосновалось.
Интерференция звука
Звук, как и любые другие колебания, может не только резонировать, но и создавать более сложные картины. Например, в случае, когда мы имеем звуковые колебания одной частоты и разности фаз, будет происходить интерференция звука.
Колебания будут складываться, и суммарная звуковая волна будет зависеть от того, как расположены по отношению друг к другу волновые фазы. В точках, где фазы волн будут одинаковы, их амплитуда будет максимальна, а в противофазе их амплитуда будет равна нулю.
То есть будут места, где звук будет очень громким, а в некоторых местах будет стоять тишина, несмотря на прохождение через это место звуковых волн. Но это можно наблюдать в основном в лаборатории, так как в жизни практически не приходится встречать подобные ситуации, когда мы имеем звуковые волны одинаковых частот и разности фаз без присутствия посторонних звуков.
Источник
Гитаростроение
|       Автор: Jhav       Дата публикации: 10 января 2013 г. |
Эта статья просто напрашивалась на написание, ибо тема лежит на поверхности, но до сих пор детально не рассмотрена. Российские и постсоветские мастера, производя хорошие инструменты, зачастую не могут объяснить природу звука их инструментов, рассказывая о «мастерстве», клеях, естественной сушке, лаках на основе природных смол и пр. А когда случается фэйл (чаще всего он постигает эксперименты мастера), то объясняется это обычно неудачным материалом. Разве не возникает желание контролировать звук будущего инструмента ДО момента выбора древесины и конструкции? ТОЧНО ЗНАТЬ, а не рисовать в воображении «рамки звучания» инструмента, путая себя и пугая клиента? Точное знание предполагает некие численные показатели и критерии; без них точное знание перестает быть знанием, а становится домыслом или, в лучшем случае, умозрительным заключением.
Я решил систематизировать знания и данные, касающиеся акустики цельнокорпусных гитар. Признаться, я начинал статью раза три, но, углубляясь в анализ, находил что-то, что заставляло меня возвращаться к самому началу. Собственно, начнем с самого начала.
Необходимое уточнение. Данная статья написана больше для меня самого, чтобы отчетливее все понять и разложить по полочкам. Никаких готовых рецептов не будет, так как любая наука требует самостоятельного мышления. При достаточном желании и подготовке (школьный курс физики/математики), все «рецепты» будут выведены вами за такой же срок, необходимый для понимания изложенного материала.
Распространение колебаний
Итак, что происходит такого в электрогитарах, что они все так по-разному звучат? Попробуем разобраться. Сначала для наглядности упростим модель гитары до бруска дерева со струной. Натяжение струны немного деформирует брусок. Если мы оттянем струну для извлечения звука, то сила натяжения так же немного деформирует брусок. Как только мы отпустим струну, произойдет следующее. Во-первых, струна начнет совершать свободные колебания, а во-вторых, в тот же момент, то есть до того, как звуковая волна от струны дойдет до опор, со своей собственной частотой начнет колебаться брусок. Брусок и струна будут колебаться в противофазе друг к другу. Как только поперечная волна струны достигнет опор, фаза свободных колебаний для бруска закончится, и он начнет колебаться с частотой струны.
Получив некоторое количество энергии, струна будет стремиться ее израсходовать. Часть энергии тратится струной на излучение в пространство, часть на преодоление ее собственного внутреннего сопротивления. Оставшаяся энергия передается бруску и тратится на преодоление внутреннего сопротивления бруска и излучение колебаний в пространство с поверхности. Струна, колеблясь, совершает работу по переносу массы бруска. Соответственно, чем больше масса бруска, тем больше энергии будет затрачиваться за каждый период колебания, и тем быстрее колебательное движение затухнет. Но только ли масса влияет на длительность и амплитуду колебательных движений? Если взять два одинаковых по массе бруска, один из древесины, а другой из пластилина, совершенно очевидно, что деревянный брусок будет дольше поддерживать колебательные движения. Кроме прочего, древесина отличается от пластилина упругостью. Упругость – свойство материала деформироваться обратимо, после снятия напряжений материал становится недеформированным. Сила упругости в простейшем случае описывается формулой:
где E – модуль упругости, Δx – величина деформации. Согласно третьему закону Ньютона, сила деформации бруска равна силе натяжения колеблющейся струны. Выходит, что чем выше модуль упругости, тем меньше величина деформации при той же силе. За один полупериод совершается меньшая работа по «переносу массы» бруска на расстояние Δx и преодолению внутреннего трения, а значит, затрачивается меньшее количество энергии за один полупериод, что делает расход энергии более длительным. Получается, что два физических свойства материала, масса и упругость, в удельных величинах – плотность ρ и модуль Юнга E, определяют способность материала колебаться. Эти величины объединяются в акустическую константу Ka:
Самые высокие значения акустической константы – у ели, кедра, пихты и сосны. Однако, у двух последних очень высокий разброс свойств, что ограничивает применение этих пород в изготовлении инструментов.
Как я говорил ранее, энергия струны в бруске расходуется на внутреннее трение (нагрев) и на излучение в пространство (собственно звучание). Характеристики материала, описывающие способность материала препятствовать колебательному процессу, называются внутренним сопротивлением и сопротивлением излучения. Чем выше внутреннее сопротивление, тем больше энергии будет затрачиваться на нагрев материала. Чем ниже внутреннее сопротивление, тем меньше энергии будет расходоваться на нагрев и больше – на излучение. Чем выше сопротивление излучения, тем больше энергии будет расходоваться в виде колебаний в пространство, тем выше будет амплитуда колебаний. Деки акустических гитар, например, обладают более высоким сопротивлением излучения, чем цельнокорпусные деки, поэтому звучат громче (правда, громкость обусловлена не только этим).
Теперь представим следующую ситуацию – наш брусок имеет такую же частоту собственных колебаний, что и струна. Что произойдет?
Резонанс
Произойдет резкое увеличение амплитуды колебаний бруска, вследствие совпадения частоты колебания струны с собственной частотой бруска. Это явление называется резонансом, а частота, на которой наблюдается резонанс – резонансной частотой. Что же происходит с энергией колебаний? Казалось бы, при увеличении амплитуды колебаний, увеличивается расход энергии в единицу времени, значит, длительность колебательного процесса должна сократиться, так как количество энергии в системе конечно и равно количеству энергии, переданному струне. Однако на практике наблюдается обратное явление – колебания увеличивают амплитуду и медленнее затухают. Дело в том, что на резонансных частотах система наиболее эффективно расходует энергию на колебания, а не на нагрев. На резонансных частотах отношение сопротивления излучения к внутреннему сопротивлению повышается. Почему так происходит? Дело в том, что резонансная частота f продольных волн нашего бруска нелинейно зависит от упругости материала, а точнее:
Отсюда следуют два важных вывода.
Акустическое КПД системы принимает наибольшие значения на резонансных частотах, так как на них упругость материала наиболее эффективно поддерживает колебания.
Зависимость упругости и резонансной частоты не линейна. Это объясняет разницу в длительности звучания дек разной толщины. Поясню на примере. Уменьшение толщины деки в два раза уменьшает массу деки в два раза (соответственно, в два раза уменьшается внутреннее сопротивление) и в два раза понижает резонансную частоту. Если бы соотношение упругости и резонансной частоты было линейным, то упругость деки понизилась бы так же в два раза, и в два раза понизилось бы сопротивление излучения. В таком соотношении получилось бы, что более тонкая дека расходовала бы энергию точно так же, как и более толстая. Тогда не было бы разницы в звучании акустических и электрогитар. Но поскольку резонансная частота и упругость связаны нелинейно, то уменьшение толщины деки в два раза понизит частоту в два, а упругость в четыре раза. Таким образом, отношение сопротивления излучения к внутреннему сопротивлению у такой деки будет ниже, чем у более толстой. Из-за этого возрастет амплитуда колебаний (дека станет более податливой) и увеличится расход энергии за один период колебаний, что сократит длительность колебательного процесса. Поэтому, при прочих равных, более тонкие деки акустик звучат громче, но с меньшим сустейном, чем более толстые.
Необходимо отметить, что резонанс будет наблюдаться в случае, если частота возбуждающих его колебаний ниже резонансной частоты и кратна ей в целое число раз, то есть резонансная частота будет являться гармоникой возбуждающей частоты. Если возбуждающая частота выше резонансной и кратна ей, то явление резонанса наблюдаться не будет, так как направление движения колебаний будет меняться в два раза чаще, чем у резонирующих колебаний, что приведет к их гашению. Это справедливо и в обратном направлении – брусок, резонирующий с частотой, в два раза превышающей частоту возбуждающих колебаний струны, будет ослаблять колебательные движения струны. Почему же тогда колебания струны не затухают сразу?
Все дело в добротности, характеристике, определяющей полосу резонанса и показывающей, во сколько раз запас энергии в системе больше, чем затраты энергии за один период колебаний. Добротность струны гораздо выше добротности деревянного бруска, и как колебательный элемент она в разы эффективнее. Следовательно, энергия ее собственных колебаний гораздо больше, поэтому резонанс деревянного бруска хоть и будет немного ее ослаблять, но не настолько, чтобы быстро погасить колебания.
Сколько же резонансных частот у бруска дерева? Логично предположить, что три – по одной на каждое измерение. Но это не так. Звук в твердых телах распространяется по более сложным законам, нежели в воздухе. В твердых телах есть волны сжатия/растяжения (поперечные), продольные (изгибные) волны, волны кручения и пр. Тело сложной формы, такое, как корпус электрогитары, может иметь достаточно большое количество резонансных частот, но наиболее выраженными будут резонансы изгибных волн вдоль относительно больших плоскостей и резонансы продольных волн вдоль и поперек волокон дерева.
Анизотропность древесины
Сейчас я хочу заострить ваше внимание на том факте, что мы будем рассматривать резонансы нашего бруска в направлении вдоль и поперек волокон. Почему? Дело в том, что дерево – материал анизотропный, его свойства очень зависят от расположения волокон. Модуль упругости вдоль волокон примерно в 20 раз выше модуля упругости в поперечном направлении. Необходимо заметить, что именно этот модуль используется для расчета акустической постоянной. Именно поэтому крайне важно отбирать хвойную древесину по распилу – акустическая постоянная выше в радиальном направлении.
Необходимо так же отметить, что анизотропность свойств древесины варьируется от породы к породе, поэтому инструменты из пород древесины с близкой акустической постоянной могут звучат различно.
Тембр гитарного звука
Очевидно, что физические свойства древесины влияют не только на излучение колебаний, но и на тембр звука. Каким образом?
Тембр звука – субъективная характеристика качества звука, позволяющая отличить звуки одинаковой интенсивности и высоты. Тембр характеризуется не только составом гармоник, но и характеристиками переходных процессов основного тона и обертонов, а так же негармоничность обертонов.
Еще раз рассмотрим колебания струны, но теперь с точки зрения колебательного процесса, а не энергии. Колебательный процесс принято делить на фазы, называемые еще переходными процессами. Для удобства будем называть их фазами. Первая фаза – атака, при которой амплитуда колебаний нарастает от нуля до максимального значения. После атаки наступает спад, когда амплитуда снижается до некоторого значения. С этого момента амплитуда начинает уменьшаться гораздо медленнее, эта фаза называется сустейном. И последняя фаза – затухание – колебания инструмента после того, как струна перестала колебаться. Эта фаза почти не представлена в гитарах, однако длинное эхоподобное затухание есть в звучании ситара. В рамках данной статьи мы пренебрежем этой фазой.
Итак, дергая струну, мы передаем ей импульс, заставляя ее совершать сложные колебания. Помимо основного тона рабочей части в звучании струны присутствуют гармоники основного тона и негармонические составляющие. Шумовые составляющие и колебания, частота которых не кратна основному тону, затухают гораздо быстрее собственной частоты струны и ее гармоник. Затухание шумовых и негармонических составляющих приходится на вторую фазу – спад. В спектре остаются только основной тон и его гармоники. При этом гармоники не кратны основному тону, а отличаются от расчетных значений. Причем, чем выше номер гармоники, тем больше это различие. Это явление называется негармоничностью обертонов и объясняется подвижностью опор струны и ненулевой поперечной упругостью струны. Соотношение амплитуд гармоник и их количество зависит от многих факторов: от массы, длины рабочей части, упругости, балласта (загрязнения), изломов и т.д., вплоть до места возбуждения колебаний (чем ближе к центру рабочей части, тем ярче выражен основной тон относительно гармоник). Спектральный состав звука – статическая характеристика тембра.
Но если бы тембры отличались только спектральным составом, то любые тембры получались бы из других обычной эквализацией. Однако тембры разных инструментов отличаются не только спектральным составом, но и характеристикой переходных процессов основного тона и обертонов. Другими словами, гармоники в составе тембров разных инструментов имеют не только различные относительные амплитуды, но и различные характеристики атаки-спада-сустейна-затухания.
Поскольку деревянная часть имеет гораздо меньшую добротность по сравнению со струной, то инструмент выступает, в общем-то, демпфером для струны. Огромная часть спектра струны затухает практически сразу. В составе спектра остается основной тон и гармоники, если они близки к резонансным частотам деревянной части. Как говорилось ранее, деревянная часть обязательно резонирует только в момент атаки, поскольку импульс передается так же и корпусу. В этот момент в спектральном составе атаки струны усиливаются частоты, на которых резонирует деревянная часть инструмента. После атаки для деревянной части наступает фаза вынужденных колебаний, и явление резонанса будет наблюдаться только в случае достаточной близости частот спектра струны и резонансных частот деревянной части. При этом увеличивается не только амплитуда гармоники, но и изменяется ее переходный процесс – такая гармоника будет медленнее затухать.
Таким образом, деревянная часть инструмента, имея некоторое количество резонансов, выступает в роли пассивного акустического фильтра, демпфируя одни составляющие тембра струны и усиливая другие. Причем резонанс древесины может как усиливать, так и демпфировать составляющие тембра струны. Об этом мы поговорим подробнее в другой раз.
Итак, механические свойства древесины влияют на звучание цельнокорпусных гитар. Задача гитарного мастера состоит в выявлении точной зависимости физических параметров деревянной части инструмента на общее звучание инструмента. Сложность состоит в том, чтобы формализовать субъективные характеристики, описываемые такими словами как «хороший сустейн», «взрывная атака», «плотный низ» и пр. В следующий раз мы попытаемся сделать шаг в этом направлении.
При использовании данной статьи на других Интернет-ресурсах указание автора и прямая ссылка на guitar.ru обязательна!
| 10.01.13 | Автор: Имя админа |  | |||||
|
25.12.2014, Jhav
Чем больше масса, тем больше энергии будет затрачиваться струной на 1 колебание, тем быстрее расходуется энергия струны — меньше сустейн.
В вашем случае необходимо понижение одного из резонансов инструмента. Я бы не рекомендовал ослаблять конструкцию, поэтому приемлемый способ — увеличение внутреннего объема и уменьшение диаметра голосника.
16.05.2014, Jhav
Vladimir,
Часть гитар копии, да. Но кто сказал, что они не делались с учетом акустики? Много моих решений, как по отбору пород древесины, так и по конструкции. Niigredo — почти холлоубоди гитара, сконструирована мной с нуля. Под копией дизайна может скрываться противоположность )
Опыт и чутье — это круто, но все это нарабатывается быстрее, когда точно знаешь, что ищешь, и, притом, в цифрах
21.04.2014, Jhav
>Статья, не спорю, теоретически грамотная, но я хотел бы спросить у автора, а сам он лично смастерил какой нибудь инструмент?
Источник