Музыкальная система координат
Общеизвестно, что многие взаимодействия,
имеющие место быть в окружающей нас Вселенной
имеют определённую цикличность.
И в том числе и цикличность «волнового порядка».
Данный «волновой порядок», в частности проявляется и при распространении
звука в воздушной среде, а так же при прочих.
циклических космических изысках,
в том числе и при перемещении.
видимого и не видимого нами «света».
идущего к нам на Землю от различных «Космическими светил».
Давно заметил, что видимые семь цветов радуги.
прямо таки напрашиваются на родственную соразмерность.
с семью основными музыкальными нотами в одной октаве.
Из за чего и сподобился таки.
ознакомится с информацией об «октавном строе».
Оказывается частота определённого звука в соседних октавах,
к примеру ДО в 1 октаве и ДО во 2 октаве отличается между собой
ровно в два раза.
А частота звука между всеми соседними полутонами имеет
постоянное соотношение равное 1,0595 что соответствует
значению корня из двух в двенадцатой степени.
В принципе это объясняется просто,
в октаве включая полутона имеется 12 нот.
Частота звучания нот последовательно увеличивается в 1,0595 раза.
А при перемножении 1,0595 само на себя 12 раз (12 нот),
ну или возведении 1,0595 в 12 степень.
и получается разница в 2 раза между определёнными нотами.
К примеру ДО 1 октавы и ДО 2 октавы (находящиеся в соседних октавах)
имеют двойное соотношения частот звучания.
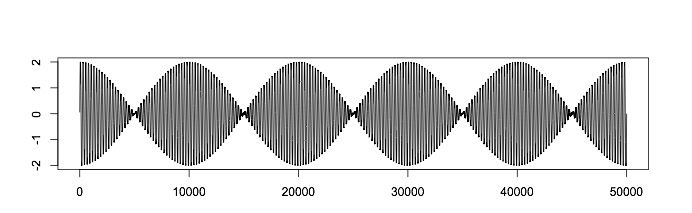
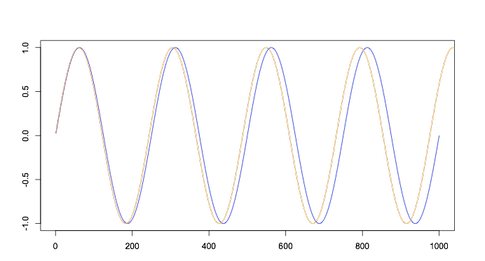
При этом направление векторов волн как видно из нижнего графика,
с «двойной периодичностью» совпадает.
Если данный «музыкальный строй» доказал состоятельность своих
пропорций, своих всевозможных «гармоник».
так сказать в воздушной среде,
то почему бы не поискать наличие данных пропорций и гармоник
для прочих «волновых скитальцев».
в пространстве Вселенной?
Вопрос скорее всего риторический, и многие многие научные мужи
им наверняка загружались, надо будет ответ списать.
Хотя есть и ещё по моему мнению ещё одна причинность для
возможного применения «музыкального ряда».
А что если прикинуть его возможности для более точного
измерения.
к примеру некой «определяемой длины»,
ведь применяемая ныне Декартовая система координат,
с использованием десятичных дробей,
к примеру при делении «простого числа» 17
на ещё более «простое число» 71
17/71
в десятичном формате измерения.
наверняка даст кучу знаков после запятой.
А ведь волны имеют целостную значимость,
и какой длины нам прикажите волну гнать.
что бы прислать сообщение в точку 17/71 .
тут однако без очень приблизительной десятичной точности.
не обойтись.
А вдруг при музыкальном.
«волновом строе» окажется возможным более точно запускать на нужное
расстояние «информационную волну»,
ну и определять конкретную длину.
с помощью октавной.
«волновой системы координат»?
Надо однако помыслить.
Далее разместил найденную в интернете информацию по данной теме,
данную с небольшими моими уточнениями.
На дорисованном мной в принципиальном формате графике нот
«ДО» 1 и 2 октавы,
я указал на явное совпадения направления векторов одноимённых
нот при наложении их совместного звучания в соседних октавах,
что по моему мнению и определяет их «одно — нотную» схожесть в звучании.
Частота, длина, амплитуда и фаза звуковой волны
Количество колебаний воздуха в секунду называется частотой звука. Волны с разной частотой воспринимаются нами как звук разной высоты: волны с малой частотой воспринимаются как низкие, басовые звуки, а волны с большой частотой — как высокие. Частота измеряется в Герцах (Гц): 1 Гц = 1 колебание в секунду; или килогерцах (кГц): 1кГц = 1000 Гц. Большинство людей от 18 до 25 лет реально способны слышать колебания воздуха с частотой от 20 до 20000 Герц (с возрастом верхняя граница восприятия уменьшается). Именно этот диапазон волн называется звуковым диапазоном. Кстати говоря, наши уши устроены таким образом, что когда мы слышим два звука, частоты которых относятся как 2:1, то нам кажется, что эти звуки близки друг к другу и при одновременном воспроизведении они для нас как бы сливаются. Именно на этом эффекте основана музыкальная шкала высоты звуков, у которой одна и та же нота повторяется каждую октаву. То есть в натуральном звукоряде частоты одинаковых нот соседних октав соотносятся между собой как 2:1.
Частота волны обратно пропорциональна длине волны — отрезку на оси распространения волны, в котором умещается полный цикл (период) изменения плотности воздуха. Чем больше частота звука, тем меньше длина волны и наоборот. Длину волны очень легко вычислить по формуле l=C/f, где C — скорость звука (340 м/с), а f — частота звуковых колебаний. Например, волна, имеющая частоту 100 Гц, имеет длину 340/100=3.4 м.
Амплитудой звуковой волны называется половина разницы между самым высоким и самым низким значением плотности. На графике амплитуде будет соответствовать разница между самой высокой (или низкой) точкой волны и горизонтальной осью графика.
НАЗВАНИЯ И ОБОЗНАЧЕНИЕ ЗВУКОВ
Из двенадцати звуков в октаве только семь имеют собственные названия
ДО РЕ МИ ФА СОЛЬ ЛЯ СИ.
Остальные пять имеют названия, образованные от основных семи,
для чего применяют специальные символы: # — диез и b — бемоль.
Диез означает, что звук расположен выше на полутон звука,
к которому он приставлен, а бемоль — ниже.
Важно помнить, что между ми и фа, как и между си и до лишь полутон,
поэтому не может быть до бемоль или ми диез.
Другая распространенная система обозначения нот — латинская:
ноты обозначаются буквами латинского алфавита C, D, E, F, G, A, H (читается «ха»).
Зная частоту любой ноты, допустим, ЛЯ первой октавы A1=440Гц
частота следующего полутона равна
частота текущего умноженная на 1,0595,
или же Fn+1=Fn умноженное на 1,0595.
Шагаем по полутонам вверх:
А1=440
А#1=A1*1,0595=440*1,0595=466 Гц
B1=A#1*1,0595=466*1,0595=493 Гц
Шагаем по полутонам вниз:
G#1=A1/1,0595=440/1,0595=415 Гц
G1=G#1/1,0595=415/1,0595=392 Гц
Повышение октавы — частота удваивается. Понижение октавы — частота делится пополам.
Коэффициент 1,0595 выводится извлечением корня двенадцатой степени
(по числу 12 нот в октаве) из числа 2.
*****
Повторное моё пояснение: если умножить число 1,0595 само на себе 12 раз (12 нот),
то в результате и получим число «2» которое и указывает
на двукратное увеличение или уменьшение частоты звука в два раза.
у одной и той же ноты находящихся в соседних октавах.
Источник
Почему некоторые ноты гармонично звучат вместе
Сохранить и прочитать потом —
Вы никогда не задумывались, почему некоторые ноты больше подходят друг другу, чем другие? Как связаны между собой частоты их волн? Почему ноты одной тональности звучат «хорошо»? Почему «хорошо» звучат ноты в составе аккорда?
Ответ на этот вопрос связан с понятием «консонанса» (т.е. «созвучия») и современной наукой психоакустикой. Консонанс представляет собой согласное, стройное звучание, а диссонанс наоборот – несогласное или беспокойное.
Прежде всего, необходимо различать чистые тона, которые являются обычными синусоидальными волнами, и реальные тона, которые воспроизводятся музыкальными инструментами. Реальные тона, по сути, состоят из гармонических обертонов с разными амплитудами. Таким образом, каждая нота, сыгранная на любом инструменте, представляет собой сложный звук, состоящий из основного тона и большого числа обертонов.
Обертоном называется любая собственная частота выше основной, а те обертоны, частоты которых относятся к частоте основного тона как целые числа, называются гармониками. При этом основной тон считается первой гармоникой. Выходит, что значения частоты каждой гармоники относятся к основному тону следующим образом: f, 2f, 3f, 4f, ….
Частоты гармоник так же относятся друг к другу как целые числа и формируют основные музыкальные интервалы: 2:1 – это октава, 3:2 – это квинта, 4:3 – это кварта и т. д. В разных музыкальных культурах и в разные периоды времени отношение к консонансным и диссонансным интервалам различалось. Во времена Пифагора консонансными интервалами считались октава, квинта и кварта, однако в 13 веке к ним присоединилась терция. Все это связано с изменением музыкальных вкусов.
Иэн Джонстон (Ian Johnston) написал книгу «Measured Tones», в которой описал теорию созвучий (музыкального консонанса). В ней он сравнивает диссонанс с приправами, отмечая тот факт, что все мы относимся к ним по-разному. Строение наших ушей и мозга отличается, потому отличаются и наши понятия о «хорошем звуке».
Лукас Бивальд (Lukas Biewald), основатель компании CrowdFlower, соглашается с тем, что «хорошее звучание» – это очень субъективное понятие. Он говорит, что то, какие песни нам нравятся, зависит от нашей культуры, характера, даже настроения.
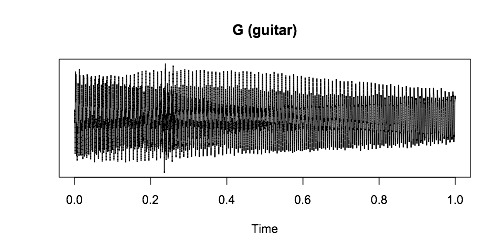
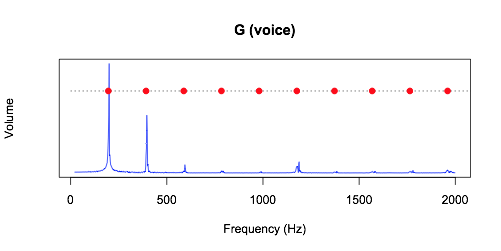
Давайте отойдем от личных предпочтений и немного углубимся в физику происходящих процессов. «Наиболее созвучными будут ноты, имеющие одинаковую высоту тона. Другими словами, соль малой октавы фортепиано созвучна с нотой соль (G) на гитаре, – отмечает Бивальд. – Вот график звуковой волны, которую воспроизводит гитарная струна»:
Звуковая волна – это серия колебаний воздуха, заставляющих вибрировать с разной частотой маленькие волосковые клетки, расположенные во внутреннем ухе человека. Слышимый нами звук являет собой сумму этих вибраций. Чтобы выделить частоты, сокрытые в этом звуке, обратимся за помощью к математике и воспользуемся преобразованием Фурье.
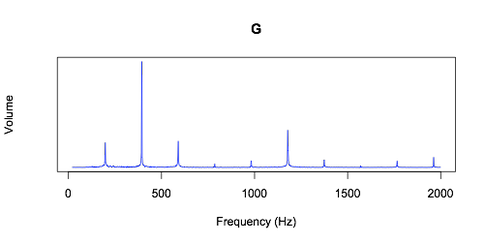
На графике мы видим, что нота соль содержит несколько частот. Самая низкая частота колебания струны равняется 196 Гц. Эта частота называется основной. Но мы видим, что есть частоты, которые превышают её в два и более раз – это обертоны или гармоники.
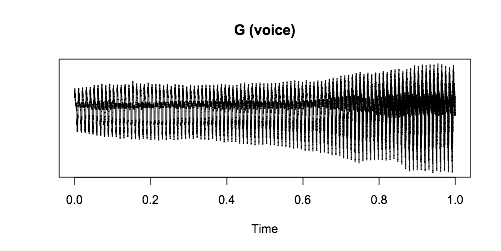
Когда Лукас Бивальд пропел ноту соль, одновременно ударяя по струне G на гитаре, получился уже вот такой график:
Внешний вид кривой отличается, но если сравнить частотные графики, то они совпадут.
Красными точками отмечены частоты гармоник. Между ними ровно 196 Гц, как и в предыдущем случае. Бивальд говорит: «Когда я пою ноту соль и беру её на гитаре, воздушные вибрации, исходящие от голосовых связок и струны инструмента, воздействуют на одни и те же волосковые клетки в моём ухе».
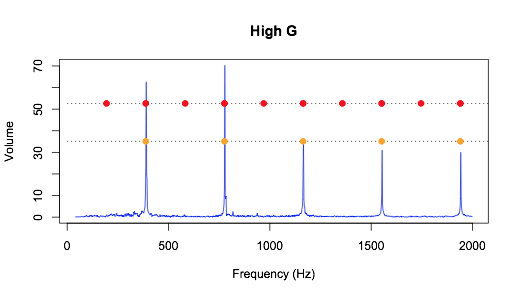
Давайте посмотрим на график, который получится, если сыграть ноту соль на гитаре, но на октаву выше. Он отличается от двух предыдущих.
Если взглянуть на частоты гармоник, то мы заметим, что положение некоторых из них совпадает. Как результат, в обоих случаях будут вибрировать практически одни и те же волосковые клетки уха. Именно поэтому у нас возникает ощущение того, что это две одинаковые ноты, хотя они и отличаются на одну октаву.
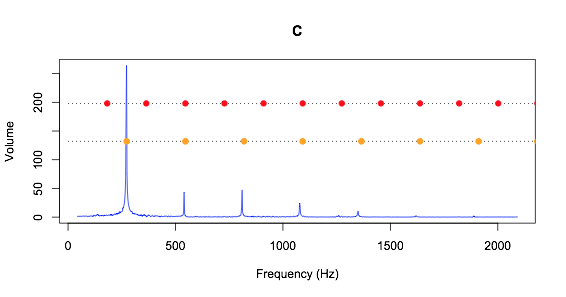
«Помимо понятия октавы у нас еще есть понятие квинты. Две ноты, которые различаются на квинту, наиболее созвучны», – говорит Бивальд. Отношение между нотами до и соль равняется квинте. Поэтому в западной музыкальной традиции большинство аккордов, строящихся от ноты до, содержат в себе ноту соль. Но почему они так подходят друг другу? Вот частоты ноты до, сыгранной на гитаре Бивальда.
Здесь красным отмечены частоты ноты соль, а жёлтым – ноты до. Видно, что они не всегда перекрываются, но поскольку основная частота ноты до относится к основной частоте ноты соль как 3/2, то совпадают каждая третья гармоника соль и каждая вторая гармоника до.
Считается, что нотами, которые наиболее созвучны с до, являются фа и соль, поскольку они находятся на расстоянии идеальной кварты и идеальной квинты соответственно. Давайте взглянем на их гармоники.
Гармоники соль и фа часто перекрывают гармоники до. Однако гармоники соль и фа совпадают на порядок реже. Именно поэтому, когда мы слышим ноты соль+до и фа+до, они кажутся нам консонансными, а когда слышим фа+соль – у нас возникает чувство диссонанса. По этой причине эти три ноты практически никогда не берутся одновременно. Теперь взглянем на более подробный график:
Видно, что у до и ми много совпадающих гармоник, поэтому ноты до, соль и ми образуют аккорд до мажор. У до и ре-диез (ми-бемоль) столько же совпадающих гармоник, поэтому ноты до, ми-бемоль и соль образуют аккорд до минор. Если гармоники нот никак друг с другом не соотносятся, то при одновременном их [нот] воспроизведении мы слышим диссонанс. Например, до и фа-диез – у них нет перекрывающихся гармоник. Подробнее об этом вы можете прочитать в другом ответе Лукаса Бивальда.
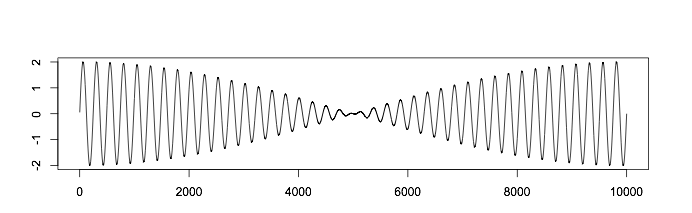
Есть и другие психоакустические эффекты, влияющие на наше восприятие звука. Диссонанс возникает в тот момент, когда мы слышим два звука с практически одинаковыми, но все же различными, частотами.
Со временем сдвиг по фазе увеличивается:
Мы с вами слышим сумму голубого и оранжевого сигналов:
Если растянуть временную шкалу, то мы получим:
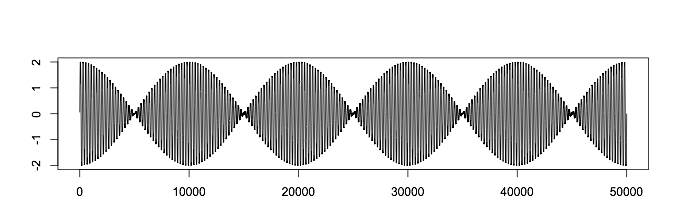
Когда сигналы находятся в фазе, они усиливают друг друга, и возникает усиливающая интерференция. По мере сдвига возникает ослабляющая интерференция, и сигналы начинают гасить друг друга до тех пор, пока не окажутся в строгой противофазе.
Из-за этого возникает пульсирующий звук, который вы наверняка слышали (сыграйте на расстроенной гитаре или фортепиано). Для западного слушателя он покажется диссонансным, но этот прием используется в музыке некоторых культур.
Источник