Какие ноты гармонично звучат

Дельта принтеры крайне требовательны к точности изготовления комплектующих (геометрия рамы, длины диагоналей, люфтам соединения диагоналей, эффектора и кареток) и всей геометрии принтера. Так же, если концевые выключатели (EndStop) расположены на разной высоте (или разный момент срабатывания в случае контактных концевиков), то высота по каждой из осей оказывается разная и мы получаем наклонную плоскость не совпадающая с плоскостью рабочего столика(стекла). Данные неточности могут быть исправлены либо механически (путем регулировки концевых выключателей по высоте), либо программно. Мы используем программный способ калибровки.
Далее будут рассмотрены основные настройки дельта принтера.
Для управления и настройки принтера мы используем программу Pronterface.
Калибровка принтера делится на три этапа:

1 Этап. Корректируем плоскость по трем точкам

Выставление в одну плоскость трех точек — A, B, C (расположенных рядом с тремя направляющими). По сути необходимо уточнить высоту от плоскости до концевых выключателей для каждой из осей.
Большинство (если не все) платы для управления трехмерным принтером (В нашем случае RAMPS 1.4) работают в декартовой системе координат, другими словами есть привод на оси: X, Y, Z.
В дельта принтере необходимо перейти от декартовых координат к полярным. Поэтому условимся, что подключенные к двигателям X, Y, Z соответствует осям A, B, C.(Против часовой стрелки начиная с любого двигателя, в нашем случае смотря на логотип слева — X-A, справа Y-B, дальний Z-C) Далее при слайсинге, печати и управлении принтером в ручном режиме, мы будем оперировать классической декартовой системой координат, электроника принтера сама будет пересчитывать данные в нужную ей систему. Это условность нам необходима для понятия принципа работы и непосредственной калибровки принтера.

Точки, по которым мы будем производить калибровку назовем аналогично (A, B, C) и позиция этих точек равна A= X-52 Y-30; B= X+52 Y-30; C= X0 Y60.

Читайте также: Пятница гимн ссср аккорд

Алгоритм настройки:

Подключаемся к принтеру. (В случае “крагозяб” в командной строке, необходимо сменить скорость COM порта. В нашем случае с 115200 на 250000 и переподключится)

После чего мы увидим все настройки принтера.
Обнуляем высоты осей X, Y, Z командой M666 x0 y0 z0.
И сохраняем изменения командой M500. После каждого изменения настроек необходимо нажать home (или команда g28), для того что бы принтер знал откуда брать отсчет.
Калибровка принтера производится “на горячую”, то есть должен быть включен подогрев стола (если имеется) и нагрев печатающей головки (HotEnd’а) (Стол 60град., сопло 185 град.) Так же нам понадобится щуп, желательно металлический, известных размеров. Для этих задач вполне подойдет шестигранный ключ (самый большой, в нашем случае 8мм, он предоставляется в комплекте с принтерами Prizm Pro и Prizm Mini)
Опускаем печатающую головку на высоту (условно) 9мм (от стола, так, что бы сопло еле касалось нашего щупа, т.к. высота пока что не точно выставлена.) Команда: G1 Z9.
Теперь приступаем непосредственно к настройке наших трех точек.
Для удобства можно вместо g- команд создать в Pronterface четыре кнопки, для перемещения печатающей головки в точки A, B, C, 0-ноль.

Последовательно перемещаясь между тремя точками (созданными ранее кнопками или командами) выясняем какая из них находится ниже всего (визуально) и принимает эту ось за нулевую, относительно нее мы будем менять высоту остальных двух точек.

Предположим, что точка A у нас ниже остальных. Перемещаем головку в точку B(Y) и клавишами управления высотой в Pronterface опускаем сопло до касания с нашим щупом, считая величину, на которую мы опустили сопло (в лоб считаем количество нажатий на кнопки +1 и +0.1)
Далее командой меняем параметры высоты оси Y: M666 Y <посчитанная величина>
M666 Y0.75
M500
G28

Ту же операцию проделываем с оставшимися осями. После чего следует опять проверить высоту всех точек, может получится, что разброс высот после первой калибровки уменьшится, но высота все равно будет отличатся, при этом самая низкая точка может изменится. В этом случае повторяем пункты 6-7.

2 Этап. Исправляем линзу

После того как мы выставили три точки в одну плоскость необходимо произвести коррекцию высоты центральной точки. Из за особенности механики дельты при перемещении печатающей головки между крайними точками в центре она может пройти либо ниже либо выше нашей плоскости, тем самым мы получаем не плоскость а линзу, либо вогнутую либо выпуклую.

Корректируется этот параметр т.н. дельта радиусом, который подбирается экспериментально.

Калибровка:

Отправляем головку на высоту щупа в любую из трех точек стола. Например G1 Z9 X-52 Y-30
Сравниваем высоту центральной точки и высоту точек A,B,C. (Если высота точек A, B, C разная, необходимо вернутся к предыдущей калибровки.)
Если высота центральной точки больше остальных, то линза выпуклая и необходимо увеличить значение дельта радиуса. Увеличивать или уменьшать желательно с шагом +-0,2мм, при необходимости уменьшить или увеличить шаг в зависимости от характера и величины искривления (подбирается экспериментально)
Команды:
G666 R67,7
M500
G28
Подгоняем дельта радиус пока наша плоскость не выровняется

3 Этап. Находим истинную высоту от сопла до столика

Третьим этапом мы подгоняем высоту печати (от сопла до нижней плоскости — столика) Так как мы считали, что общая высота заведомо не правильная, необходимо ее откорректировать, после всех настроек высот осей. Можно пойти двумя путями решения данной проблемы:
1 Способ:
Подогнав вручную наше сопло под щуп, так что бы оно свободно под ним проходило, но при этом не было ощутимого люфта,

Командой M114 выводим на экран значение фактической высоты нашего HotEnd’а
Командой M666 L получаем полное значение высоты (Параметр H)
После чего вычитаем из полной высоты фактическую высоту.
Получившееся значение вычитаем из высоты щупа.

Таким образом мы получаем величину недохода сопла до нижней плоскости, которое необходимо прибавить к полному значению высоты и и записать в память принтера командами:
G666 H 235.2
M500
G28

2 Способ:
Второй способ прост как валенок. С “потолка”, “на глаз” прибавляем значение высоты (после каждого изменение не забываем “уходить” в home), добиваясь необходимого значения высоты, но есть шанс переборщить со значениями и ваше сопло с хрустом шмякнется об стекло.

Как сделать авто калибровку для вашего принтера и что при этом авто калибрует принтер вы узнаете из следующих статей.

Источник

Почему некоторые ноты гармонично звучат вместе

Сохранить и прочитать потом —

Вы никогда не задумывались, почему некоторые ноты больше подходят друг другу, чем другие? Как связаны между собой частоты их волн? Почему ноты одной тональности звучат «хорошо»? Почему «хорошо» звучат ноты в составе аккорда?

Ответ на этот вопрос связан с понятием «консонанса» (т.е. «созвучия») и современной наукой психоакустикой. Консонанс представляет собой согласное, стройное звучание, а диссонанс наоборот – несогласное или беспокойное.

Прежде всего, необходимо различать чистые тона, которые являются обычными синусоидальными волнами, и реальные тона, которые воспроизводятся музыкальными инструментами. Реальные тона, по сути, состоят из гармонических обертонов с разными амплитудами. Таким образом, каждая нота, сыгранная на любом инструменте, представляет собой сложный звук, состоящий из основного тона и большого числа обертонов.

Обертоном называется любая собственная частота выше основной, а те обертоны, частоты которых относятся к частоте основного тона как целые числа, называются гармониками. При этом основной тон считается первой гармоникой. Выходит, что значения частоты каждой гармоники относятся к основному тону следующим образом: f, 2f, 3f, 4f, ….

Частоты гармоник так же относятся друг к другу как целые числа и формируют основные музыкальные интервалы: 2:1 – это октава, 3:2 – это квинта, 4:3 – это кварта и т. д. В разных музыкальных культурах и в разные периоды времени отношение к консонансным и диссонансным интервалам различалось. Во времена Пифагора консонансными интервалами считались октава, квинта и кварта, однако в 13 веке к ним присоединилась терция. Все это связано с изменением музыкальных вкусов.

Иэн Джонстон (Ian Johnston) написал книгу «Measured Tones», в которой описал теорию созвучий (музыкального консонанса). В ней он сравнивает диссонанс с приправами, отмечая тот факт, что все мы относимся к ним по-разному. Строение наших ушей и мозга отличается, потому отличаются и наши понятия о «хорошем звуке».

Лукас Бивальд (Lukas Biewald), основатель компании CrowdFlower, соглашается с тем, что «хорошее звучание» – это очень субъективное понятие. Он говорит, что то, какие песни нам нравятся, зависит от нашей культуры, характера, даже настроения.

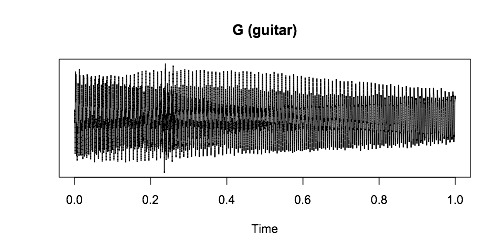
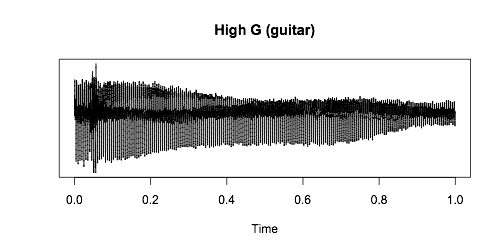
Давайте отойдем от личных предпочтений и немного углубимся в физику происходящих процессов. «Наиболее созвучными будут ноты, имеющие одинаковую высоту тона. Другими словами, соль малой октавы фортепиано созвучна с нотой соль (G) на гитаре, – отмечает Бивальд. – Вот график звуковой волны, которую воспроизводит гитарная струна»:

Звуковая волна – это серия колебаний воздуха, заставляющих вибрировать с разной частотой маленькие волосковые клетки, расположенные во внутреннем ухе человека. Слышимый нами звук являет собой сумму этих вибраций. Чтобы выделить частоты, сокрытые в этом звуке, обратимся за помощью к математике и воспользуемся преобразованием Фурье.

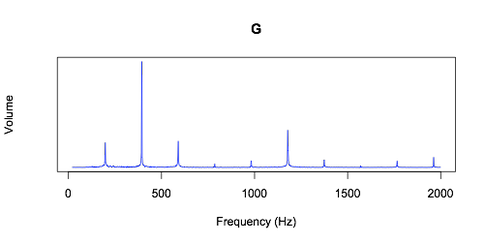
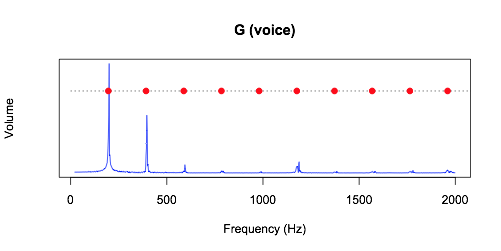
На графике мы видим, что нота соль содержит несколько частот. Самая низкая частота колебания струны равняется 196 Гц. Эта частота называется основной. Но мы видим, что есть частоты, которые превышают её в два и более раз – это обертоны или гармоники.

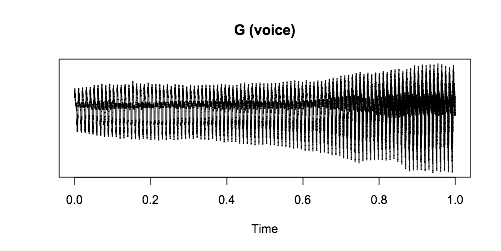
Когда Лукас Бивальд пропел ноту соль, одновременно ударяя по струне G на гитаре, получился уже вот такой график:

Внешний вид кривой отличается, но если сравнить частотные графики, то они совпадут.

Красными точками отмечены частоты гармоник. Между ними ровно 196 Гц, как и в предыдущем случае. Бивальд говорит: «Когда я пою ноту соль и беру её на гитаре, воздушные вибрации, исходящие от голосовых связок и струны инструмента, воздействуют на одни и те же волосковые клетки в моём ухе».

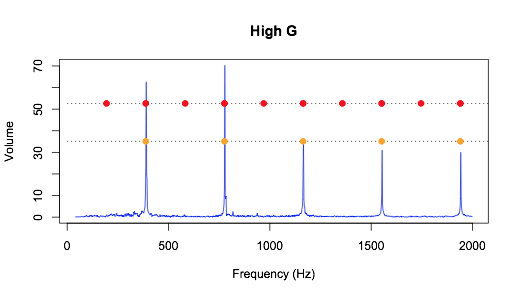
Давайте посмотрим на график, который получится, если сыграть ноту соль на гитаре, но на октаву выше. Он отличается от двух предыдущих.

Если взглянуть на частоты гармоник, то мы заметим, что положение некоторых из них совпадает. Как результат, в обоих случаях будут вибрировать практически одни и те же волосковые клетки уха. Именно поэтому у нас возникает ощущение того, что это две одинаковые ноты, хотя они и отличаются на одну октаву.

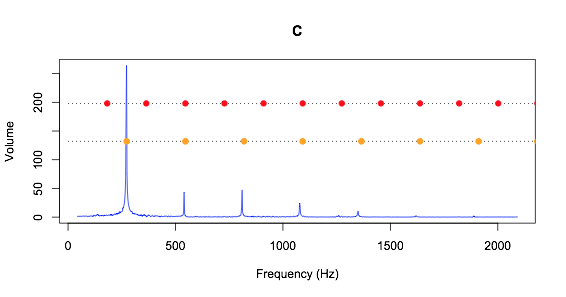
«Помимо понятия октавы у нас еще есть понятие квинты. Две ноты, которые различаются на квинту, наиболее созвучны», – говорит Бивальд. Отношение между нотами до и соль равняется квинте. Поэтому в западной музыкальной традиции большинство аккордов, строящихся от ноты до, содержат в себе ноту соль. Но почему они так подходят друг другу? Вот частоты ноты до, сыгранной на гитаре Бивальда.

Здесь красным отмечены частоты ноты соль, а жёлтым – ноты до. Видно, что они не всегда перекрываются, но поскольку основная частота ноты до относится к основной частоте ноты соль как 3/2, то совпадают каждая третья гармоника соль и каждая вторая гармоника до.

Считается, что нотами, которые наиболее созвучны с до, являются фа и соль, поскольку они находятся на расстоянии идеальной кварты и идеальной квинты соответственно. Давайте взглянем на их гармоники.

Гармоники соль и фа часто перекрывают гармоники до. Однако гармоники соль и фа совпадают на порядок реже. Именно поэтому, когда мы слышим ноты соль+до и фа+до, они кажутся нам консонансными, а когда слышим фа+соль – у нас возникает чувство диссонанса. По этой причине эти три ноты практически никогда не берутся одновременно. Теперь взглянем на более подробный график:

Видно, что у до и ми много совпадающих гармоник, поэтому ноты до, соль и ми образуют аккорд до мажор. У до и ре-диез (ми-бемоль) столько же совпадающих гармоник, поэтому ноты до, ми-бемоль и соль образуют аккорд до минор. Если гармоники нот никак друг с другом не соотносятся, то при одновременном их [нот] воспроизведении мы слышим диссонанс. Например, до и фа-диез – у них нет перекрывающихся гармоник. Подробнее об этом вы можете прочитать в другом ответе Лукаса Бивальда.

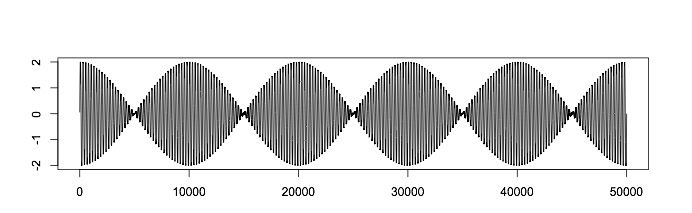
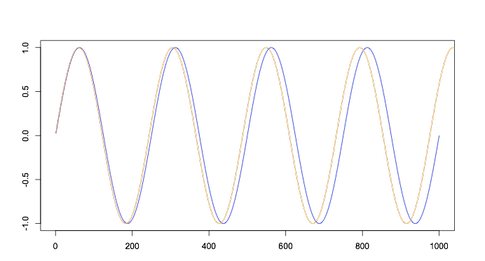
Есть и другие психоакустические эффекты, влияющие на наше восприятие звука. Диссонанс возникает в тот момент, когда мы слышим два звука с практически одинаковыми, но все же различными, частотами.

Со временем сдвиг по фазе увеличивается:

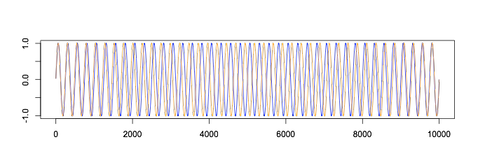
Мы с вами слышим сумму голубого и оранжевого сигналов:

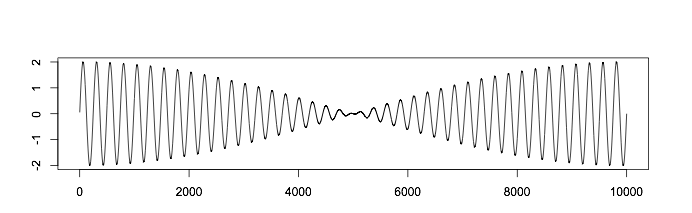
Если растянуть временную шкалу, то мы получим:

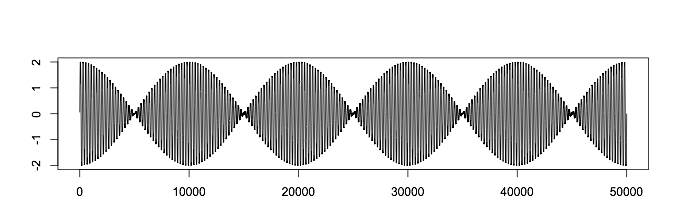
Когда сигналы находятся в фазе, они усиливают друг друга, и возникает усиливающая интерференция. По мере сдвига возникает ослабляющая интерференция, и сигналы начинают гасить друг друга до тех пор, пока не окажутся в строгой противофазе.

Из-за этого возникает пульсирующий звук, который вы наверняка слышали (сыграйте на расстроенной гитаре или фортепиано). Для западного слушателя он покажется диссонансным, но этот прием используется в музыке некоторых культур.

Источник