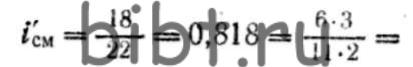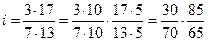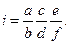Конструкция гитары сменных зубчатых колес

§ 3. МЕТОДЫ ПОДБОРА СМЕННЫХ КОЛЕС ГИТАР.

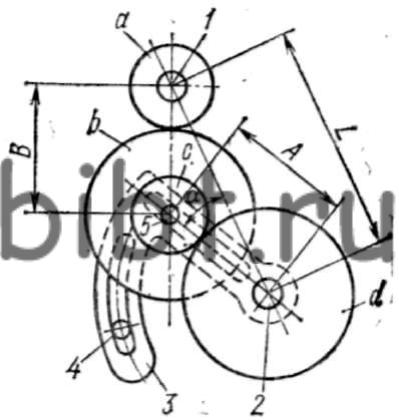
(рис. 2) называется устройство, обеспечивающее правильное сцепление сменных зубчатых колес.

Рис. 2. Схема двухпарной гитары

Расстояние L между ведущим 1 и ведомым 2 валами является неизменным. На ведомом валу свободно установлен приклон гитары 3, закрепленный болтом 4. Ось 5 промежуточных колес b,с можно перемещать по радиальному пазу, тем самым изменяя расстояние А между центрами колес с и d. Дуговой паз позволяет регулировать размер В. Чтобы подобранные сменные зубчатые колеса не упирались во втулки валов 1, 2, необходимо соблюдать условия их сцепляемости:

При подборе колес необходимо учитывать и допускаемые пределы передаточных отношений пар сменных колес 1/5 с+(15-:-20) или 60+70>40+15;

c+d>b+(15-:-20) или 40+80>70+15.

Способ замены часто встречающихся чисел приближенными дробями заключается в том, что часто встречающиеся при нарезании дюймовых резьб, червяков и в других случаях числа π и 25,4 (числовое значение дюйма) заменяют приближенными значениями, удобными для подбора сменных колес, например:

1» ≈ 25,4 мм =127/5 мм; π≈22/7≈(19*21)/127 и т.д.

Полученная при этом погрешность не должна превышать заданной по условию. Абсолютная погрешность наладки

относительная погрешность наладки

где i см — заданное передаточное отношение; i’ см — полученное передаточное отношение сменных колес.

Способ подбора сменных колес на логарифмической линейке наименее точен. Край движка логарифмической линейки устанавливают против числа, соответствующего передаточному отношению гитары сменных колес. Передвижением бегунка находят риски, совпадающие на движке и на линейке. По полученным новым целым числам, которые дают при делении те же значения частного, подбирают числа зубьев сменных зубчатых колес:

и т. д.

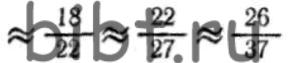
Выбирают наиболее точные и удобные значения i’ см для подбора колес: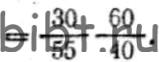. Затем подсчитывают абсолютную погрешность ∆i= 0,818 — 0,817 = 0,001; относительную погрешность δ=0,001/0,817=0,0012239.

Способ подбора сменных колес по таблицам очень точен, но его следует применять лишь в тех случаях, когда нельзя подобрать колеса методом разложения на сомножители. Наиболее быстрый подбор сменных колес можно выполнить по таблицам, приведенным в работе [22].

Источник

Большая Энциклопедия Нефти и Газа

Гитара — сменное зубчатое колесо

Гитары сменных зубчатых колес применяются на токарных, зуборезных, затыловочных, фрезерных и других станках, а также в делительных головках. [1]

При построении графика чисел оборотов для однопарной гитары сменных зубчатых колес проводят две вертикальные линии / и / /, соответствующие двум валам гитары. Этот график составлен для гитары, обеспечивающей восемь ступеней чисел оборотов. [2]

С вала VIII вращение передается через гитару сменных зубчатых колес ( и a / b — c / d) на вал IX коробки подач. При и a / b — c / d 40 / 86 — 86 / 64 нарезают метрические и дюймовые резьбы, а также получают табличные значения продольных и поперечных подач суппорта, а при и a / b — c / d 60 / 73 — 86 / 36 нарезают модульные и питчевые резьбы. [3]

От вала 85 движение передается через гитару сменных зубчатых колес 95 на ходовой винт станка 21, который при помощи гайки 22 перемещает стол станка. [4]

На рис. 31, а показана схема гитары сменных зубчатых колес . Эта простейшая передача обеспечивает настройку на большой диапазон подач. На рис. 31, б показана схема механизма с вытяжной шпонкой. [6]

В цепи главного движения станка поставлена коробка скоростей в сочетании с гитарой сменных зубчатых колес . [7]

Некоторые модернизированные зубофре-зерные станки, кроме перечисленных четы — / рех гитар, имеют пятую гитару сменных зубчатых колес . [8]

Для получения двух величин рабочих подач на головках устанавливают две электромагнитные муфты и соответственно две гитары сменных зубчатых колес . [10]

Первая цепь приводится во вращение от центрального вала через цепную передачу г 25 и z 29, гитару сменных зубчатых колес В к Г, червячную передачу К. [11]

Кинематическая цепь главного движения осуществляется от электродвигателя через зубчатые колеса zl-z 2 — г3 — z4, гитару сменных зубчатых колес А и Б, конические зубчатые колеса z5 — 26, зубчатое колесо z7, три паразитных зубчатых колеса zg на зубчатое колесо с внутренним z9 и наружным z10 зацеплением. Это колесо является центральным. От него вращение через зубчатое колесо zu, синхронизатор, z12, z13 передается на шпиндель. Число оборотов шпинделя во всех позициях здесь одинаковое. [12]

Для обеспечения требуемых скоростей вращения и поступательного перемещения фрезы и заготовки в процессе нарезания зубьев станок имеет четыре гитары сменных зубчатых колес . [14]

Источник

Гитары сменных зубчатых колес

Гитара – это механизм со сменными зубчатыми колесами, предназначенный для ступенчатого изменения передаточного отношения расчетной кинематической цепи. Они применяются в основном в редко перенастраиваемых цепях при большом диапозоне и количестве передаточных отношений органа настройки расчетной цепи. Эти механизмы отличаются простотой конструкции. Основной недостаток гитар – трудоемкость настройки.

В станках используют гитары с одной, двумя и тремя парами сменных зубчатых колес. Гитара с одной парой сменных зубчатых колес (см. рис. 1.2) применяется в основном в цепях, не требующих точной настройки (органы настройки i_v и i_s). Гитары с двумя и тремя парами сменных зубчатых колес используются, как правило, для точной настройки кинематических цепей (органы настройки i_x, i_y и т.п.). На рис. 2.19 показаны гитары с двумя и тремя парами сменных зубчатых колес.

Гитара с двумя парами колес (рис.2.19,а) состоит из плиты 1, оси 2, фиксирующего болта 3 и сменных зубчатых колес a, в, c, d. Поскольку сумма зубьев сцепляемых колес при различных настройках различна, в плите гитары предусмотрен паз, позволяющий перемещать ось 2 и таким образом осуществлять зацепление сменных колес c и d различных диаметров. Болтом 3 фиксируют плиту гитары в требуемом положении для сцепления колес а и в.

Для подбора зубчатых колес пользуются единственным уравнением с четырьмя неизвестными

, (*)

где i – передаточное отношение, полученное по ФН; a, b, c, d — числа зубьев колес гитары.

Число решений уравнения (*) ограничено следующими факторами:

— имеющимся набором сменных зубчатых колес;

а + в > с + (15…20) (**); с +d > в + (15…20) (***).

Для подбора сменных зубчатых колес используют в основном два следующих метода: основной и дополнительный.

Рис. 2.19. Гитары сменных зубчатых колес: а – с двумя парами

сменных колес; б – развертка гитары с двумя парами сменных

колес; в — гитара с тремя парами сменных колес

Основной метод – разложение на простые множители. Используется, когда i выражается простой дробью, числитель и знаменатель которой разлагаются на простые множители, удобные для подбора колес. Например,

.

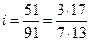
Допустим, что в наборе сменных зубчатых колес станка имеются колеса с числами зубьев, кратными пяти от 20 до 100. Тогда,

Проверяем условия сцепляемости (**) по допустимому зачению

Возможно, что зубчатое колесо будет перерезать ведомый вал (рис.2.19,б) и, следовательно, монтаж колес невозможен. Поменяем местами колеса в числителе или знаменателе. Например,

.

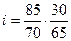
Проверяем условия сцепляемости по большему допустимому значению: (**) 85 + 70 > 30 + 20; (***) 30 + 65 > 70 + 20.

Условия сцепляемости подтверждают возможность монтажа подобранных сменных зубчатых колес в гитаре.

Дополнительный метод – приближенный подбор. В этом случае используют способ непрерывных дробей или чаще табличный метод.

Пусть по формуле настройки i = 0, 309329. По таблицам (см., например, М.В. Сандаков и др. Таблицы для подбора шестерен: Справочник. – 6-е изд. М.: 1988. – 571 с.) подбираем соответствующую этой десятичной дроби простую дробь. После преобразований получим числа зубьев сменных колес

.

Такие зубчатые колеса имеются в нормальном наборе сменных зубчатых колес, например, зубофрезерных станков. Проверяем условия сцепляемости: (**) 21 + 65 > 45 + 20; (***) 45 + 47 > 65 + 20.

В ряде станков, например зубофрезерных, как правило, предусматривается более широкий диапозон настройки кинематических. Поэтому в таких станках используются гитары с тремя парами сменных зубчатых колес. В этих гитарах (рис.2. 19,в) используется дополнительная пара зубчатых колес, а в ее плите выполняется два или три паза для промежуточных осей. Для подбора зубчатых колес используется уравнение с шестью неизвестными

Зубчатые колес e и f меняются значительно реже, чем колеса а,в,с,d. Как правило их передаточное отношение постоянно и равно 1; 1/2; 2. Это позволяет для данной пары колес использовать только четыре сменных зубчатых колеса, например с числами зубьев 40, 60, 60, 80.

Колеса а, в, с, d подбираются по правилам подбора колес для двухпарной гитары, а к условиям сцепляемости добавляется еще одно

Для различных групп станков комплекты сменных зубчатых колес различны. Однако все комплекты создаются на основе общего ряда чисел зубьев сменных колес: 20 – 23 — 25 – 30 – 33 – 34 – 37 – 40 — 41 – 43 – 45 – 47 – 50 – 53 – 55 – 58 – 59 – 60 – 62 – 65 – 67 – 70 – 71 – 73 -75 – 79 – 80 — 83 – 85 – 89 – 90 – 92 – 95 – 97 – 98 – 100 – 105 – 113 – 115 – 120 – 127 — всего 44 колеса.

Для токарно-винторезных станков принят набор колес, у которых числа зубьев кратны пяти (в комплекте 22 колеса).

Набор зубчатых колес для зуборезных станков ограничен колесом с числом зубьев 100. В затыловочных станках набор колес аналогичен общему, но в нем нет колеса со 113 зубьями. Для фрезерных станков (для настройки делительных головок) набор состоит из колес с числами зубьев: 25 – 25 – 30 – 35 – 40 – 50 – 55 – 60 – 70 – 80 – 90 – 100 (всего 12 колес).

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Для чего на токарных станках нужны дополнительные шестерни к гитаре сменных колес?

Раньше на большинстве предприятий гитару дефференциала считали технологи (по крайней мере насколько я это знаю). На данный момент на некоторых предприятиях дифференциал считают технологи, а на некоторых эта «забота» перешла к зуборезчикам, что уж и говорить когда требуется «втихаря» сделать шабашку! Связанно это думаю с тем, что с массового производства шестернь идёт переход на производство на малых предприятиях, где эта задача ложится на плечи зуборезчика… Лично моё мнение и я не раз уже говорил об этом — считать дифференциал должны технологи, хотя данное умение не помешает зуборезчику. Конечно это не трудно, но зачем лишняя ответственность? Я думаю Вы со мной согласитесь. В основном никто просто не хочет брать на себя ответственность!

«Ручной» подбор колес гитары дифференциала.

Значение передаточного отношения (u) представляем приближениями в виде обычных дробей.

u=0,184584124≈5/27≈12/65≈79/428≈91/493≈6813/36910

Это можно сделать при помощи программы для представления многозначных констант приближениями в виде дробей с заданными точностями или в Excel подбором.

Выбираем подходящую по точности дробь и раскладываем ее числитель и знаменатель на произведения простых чисел. Простые числа в математике – это те, что делятся без остатка только на 1 и на себя.

u’=91/493=0,184584178

91/493=(7*13)/(17*29)

Умножаем числитель и знаменатель выражения на 2 и на 5. Получаем результат.

Z1=26 Z2=85 Z3=35 Z4=58

Вычисляем относительную погрешность выбранного варианта.

δ=|(u-u’)/u|*100=|(0,184584124-0,184584178)/0,184584124| *100=0,000029%

1. Станина аппарата.
2. Коробка переключения скоростей.
3. Распределительный механизм.
4. Валик ручного перемещения каретки.
5. Управление механическим перемещением каретки.
6. Делитель.
7. Панель управления.
8. Стойка, которая крепится на станине.
9. Ограничитель движения каретки.
10. Ограничитель движения каретки.
11. Каретка.
12. Кран подачи охлаждающей жидкости.
13. Суппорт.
14. Кронштейн.
15. Контрподдержка.
16. Управление перемещением кронштейна.
17. Подающий стол.
18. Механизм управления ограничителями каретки.
19. Механизм управления перемещением стола.
20. Упор подвода стола.
21. Кран управления смазкой стола.
22. Упор подвода стола.
23. Обрабатываемая заготовка.
24. Фреза для нарезки зуба.

На схеме отсутствует место расположения главного электрического двигателя, приводящего в движение фрезу для нарезки зуба и подающий стол, на который устанавливается обрабатываемая деталь.

Особенностью данного станка является наличие отдельного электродвигателя, роль которого заключается в непрерывной работе транспортера, удаляющего стружку, образующуюся в процессе обработки.

Вращение фрезы – основное движение при обработке заготовки. Нарезка по всей длине выполняется за счет движения цилиндрического элемента вокруг своей оси. Для получения расчетного количества зубов скорость вращения подающего стола синхронизируется с количеством оборотов и передаточным отношением гитары.

Настройка гитары по таблицам справочника.

С помощью таблиц справочника М.И. Петрика и В.А. Шишкова «Таблицы для подбора зубчатых колес» можно быстро решить рассматриваемую задачу. Методология работы подробно и понятно описана в самом начале книги.

Стандартный комплект В.А. Шишкова содержит 29 зубчатых колес с числами зубьев: 23; 25; 30; 33; 37; 40; 41; 43; 45; 47; 50; 53; 55; 58; 60; 61; 62; 65; 67; 70; 73; 79; 83; 85; 89; 92; 95; 98; 100.

Используем этот набор в решении нашей задачи.

Результат подбора по таблицам:

Z1=23 Z2=98 Z3=70 Z4=89

u’=(23*70)/(98*89)=0,184590690

δ=|(u-u’)/u|*100=|(0,184584124-0,184590690)/0,184584124| *100=0,003557%

Расчёт гитары деления. Как посчитать?

Расчёт гитары деления на зубофрезерный станок, пожалуй одно из самых необходимых действий при настройки станка. Считать гитару деления должен уметь каждый зуборезчик (на некоторых предприятиях в чертежах написана гитара деления).

Основная формула для расчётов — это отношение постоянной станка к количеству зубьев нарезаемой детали: c деления/количество зубьев. К примеру если постоянная станка 24, а нам необходимо нарезать 99 зубьев, то гитара деления будет выглядеть так — 24/99 (a/b). Ведущая шестерня 24, а ведомая 99. Иногда приходится разлаживать числа, так как шестерни могут не соединиться или постоянная такая что не поставишь, например есть постоянная 10, или число зубьев большое — от 127 и больше. Тогда гитара деления выглядит так — a/b c/d/. Шестерня a соединяется с шестерней b, которая на одном валу с шестерней c, шестерня c соединяется с шестерней d. Есть чуть другой вариант, главное что бы числитель не соединялся с числителем, а знаменатель со знаменателем и передаточное число соответствовало основному варианту — a/b. Всё это понятней на видео которое я сделал для вас:

Какие постоянные у зубофрезерных станков? Сильно долго не буду вникать в это, сразу по быстрому, постоянные которые знаю из личного опыта: 10, 15, 20, 24, 25, 30, 48, 60, 72. А вот к примеру постоянная на зубодолбёжном станке разная, это количество зубьев на долбяке.

В некоторых случаях гитара деления берётся из таблиц. К примеру на рейкофрезерный станок. На данном станке получается именно шаг определённого модуля. К примеру при обкатке или единичном делении на обычном зубофрезерном станке получается тоже шаг, но он получается путём деления окружности на равные части. В случаем же с рейкой — она может быть условно бесконечной, поэтому тут расчёт чуть другой именно на шаг. Таблица гитары деления на реечный станок, должна быть в паспорте данного станка.

Так же гитара деления считается по другим формулам, а проще взять сразу с таблица, на некоторые зарубежные станки. Например я сейчас начал работать на немецком зубофрезерном станке GFL там есть таблица.

Давайте я вам покажу на изображениях как считать гитару деления. К примеру посчитаем гитару деления с постоянной станка — 10, число зубьев — 60.

Давайте возьмём вариант чуть посложней, постоянная станка — 30, а нарезать надо 366 зубьев. Гитара деления будет с паразиткой (паразитка любая удобная шестерня которая служит для изменения вращения и не влияет на передаточное число). Итак:

В этом случае можно посчитать чуть по другому, но принцип не меняется.

Если есть вопросы, пишите в комментариях!

Требуется зуборезчик в Санкт-Петербурге.

Требуется зуборезчик. Киев.

Гитара дифференциала в режиме on-line.

Заходите на сайт по адресу: sbestanko.ru/gitara.aspx и, если ваша модель станка присутствует в списке исходных данных, то задаете параметры нарезаемого колеса и червячной фрезы и ждете результат расчета. Иногда считает долго, иногда не находит решений.

Для нашего примера сервис не представил решений для точностей 5 и 6 разрядов после запятой. Зато для точности 4 знака после запятой выдал 136 вариантов. Мол — ковыряйтесь!

Лучший из представленных on-line сервисом результатов:

Z1=23 Z2=89 Z3=50 Z4=70

u’=(23*50)/(89*70)=0,184590690

δ=|(u-u’)/u|*100=|(0,184584124-0,184590690)/0,184584124| *100=0,003557%

Источник

Читайте также:  Висков ноты для хора