- Обращение интервалов от ноты си бемоль
- Обращение интервалов от ноты си бемоль
- ОБРАЩЕНИЕ ИНТЕРВАЛОВ
- Консонирующие и диссонирующие интервалы
- Проверка:
- Тестовое занятие
- Соль-фа.рф
- Интервалы от ноты си
- Простые интервалы от ноты си:
- Составные интервалы от ноты си:
- Интервалы.
- Обращение интервалов или волшебство на уроках сольфеджио
- Как выполняются обращения интервалов?
- Законы обращения интервалов
- Проверь себя!
- Фокусы с составными интервалами
- Применение обращений интервалов
Обращение интервалов от ноты си бемоль
Сайт для учеников Е. А. Климина . и не только
Обращение интервала – интервал, который образуется в результате перемещения основания исходного интервала на октаву выше или вершины – на октаву ниже.
Как это делается:
1) Берется исходный интервал; 



Прима 1 – Октава 8 Секунда 2 – Септима 7 Терция 3 – Секста 6 Кварта 4 – Квинта 5 Большая – Малая Чистая – Чистая Октава 8 – Прима 1 Септима 7 – Секунда 2 Секста 6 – Терция 3 Квинта 5 – Кварта 4 Малая – Большая Чистая – Чистая
Увеличенная – Уменьшенная Уменьшенная – Увеличенная
Обращение малого интервала всегда будет большим, обращение большого – малым. Обращение чистого интервала будет тоже чистым. Обращение увеличенного интервала – уменьшенным.
Если сложить вместе цифры (ступеневые величины) интервала и его обращения, во всех случаях получится 9.
Примеры обращений интервалов от ноты До: начальный уровень.
Примеры обращений интервалов от ноты До: продвинутый уровень (наиболее продвинутый включает в себя также уменьшенные кварты и уменьшенные квинты, которые проходятся отдельно в старших классах) .
Источник
Обращение интервалов от ноты си бемоль
Интервал от ноты соль вверх
Интервал от ноты до вниз
Интервал от ноты ля вниз
Интервалы также называют мелодическими или гармоническими.
В ГАРМОНИЧЕСКОМ интервале звуки пишутся друг над другом и звучат одновременно.
В МЕЛОДИЧЕСКОМ интервалы звуки пишутся друг над другом и звучат поочередно.
В гармонических интервалах знаки пишутся слева от всего интервала. Знак ставится напротив ноты.
Название интервала (прима, секунда. ) всегда зависит только от нот и не меняется в зависимости от количества полутонов между звуками. Ноты дают название интервалу, количество полутонов уточняет интервал.
Пример: рассмотрим всё ту же секунду, ноты «до» и «ре». Итак, несколько вариантов:
«до» — «ре диез» — увеличенная секунда (полтора тона). Энгармонически равна малой терции, но таковой не является (почему?);
«до» — «ре» — большая секунда (целый тон);
«до» — «ре бемоль», малая секунда (полутон);
«до» — «ре дубль бемоль», уменьшённая секунда (0 тонов). Энгармонически равна чистой приме, но называется секундой, поскольку «до» и «ре» — это секунда. Прима — это «до»-«до», «ре»-«ре» и т.д.
В дальнейшем вы будете использовать знания интервалов в аранжировках собственных песен, и при импровизационной игре на инструменте. Знание тональностей и последовательностей аккордов сделают вашу музыку насыщенной и разнообразной.
ОБРАЩЕНИЕ ИНТЕРВАЛОВ
Обращение интервала — перемещение звуков интервала на октаву, при котором его основание становится верхним звуком, а вершина — нижним.
Основание в интервале– это нижняя нота интервала, вершина – это верхняя нота интервала. Обращение простых интервалов (в пределах октавы) производится двумя способами: перенесением основания интервала на октаву вверх или вершины на октаву вниз.
В результате таких изменений образуется новый интервал.
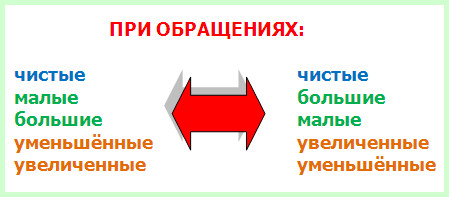
Есть закономерность: чистые интервалы обращаются в чистые, большие — в малые, малые — в большие, увеличенные — в уменьшённые, уменьшённые — в увеличенные.
Приведем пример: возьмём большую терцию «до-ми» и обратим её любым способом. Сначала, основание «до» перенесём на октаву вверх, у нас получится интервал «ми-до» — малая секста. Затем попробуем поступить наоборот и перенесём вниз на октаву верхний звук «ми», в результате также получаем малую сексту «ми-до». На картинке желтым цветом выделен звук, который остаётся на месте, а сиреневым – тот, который перемещается на октаву.
Обращение на нотном стане записывается так:
Обращение интервалов нужны для интонирования звуков. Для лучшего результата нужно пропевать построенный интервал и безошибочно попадать в ноты обращенного вида. Это тренирует слух, помогает точно подобрать интервалы, аккорды и соло в музыке.
Сочетание двух мелодий, звучащих одновременно, часто изменяется путем передвижения на октаву так, что верхняя мелодия становится нижней, а нижняя — верхней. При этом все интервалы, образующиеся между мелодиями, обращаются:
Такой прием называется двойным контрапунктом октавы (двойным, т. к. мелодий две и у каждой из них два положения, одно сверху, а другое снизу; контрапунктом — потому, что так называется сочетание мелодий, звучащих одновременно; октавы —по интервалу, на который переносятся мелодии).
Практическая область применений обращений связана не только с пониманием того, как возникли некоторые интервалы (да-да, исторически некоторые интервалы были обнаружены путём обращения). Если брать теоретическую область, то обращения очень помогают, например, в понимании устройства некоторых аккордов.
Если брать область творческую, то обращения широко применяются при сочинении музыки, причём иногда мы даже их не замечаем. Послушайте, например, кусочек красивой мелодии в романтическом духе, он весь построен на восходящих интонациях терций и секст.
Консонирующие и диссонирующие интервалы
Словом «консонанс» обозначают сливающееся звучание. Это то созвучие, которое хорошо ложится на слух.
Словом «диссонанс» обозначают разнозвучие. Это то, что режет слух. Те звуки, которые вместе «не звучат».
Консонансы подразделяются на три вида:
- абсолютные консонансы, к которым относятся интервалы чистой примы и чистой октавы;
- совершенные консонансы, к которым относятся чистая квинта и, отчасти, чистая кварта;
- несовершенные консонансы, к которым относятся большие и малые терции и большие и малые сексты.
Диссонансы: все остальные интервалы, а именно — большие и малые секунды, большие и малые септимы и тритоны (увеличенная кварта или уменьшенная квинта), хотя степень их диссонирования тоже не одинакова. Например, у малой септимы она значительно меньше, нежели у большой септимы. Наиболее же резким из всех диссонансов является малая секунда.
Проверка:
-
- Определить название интервалов
Достроить интервал (стрелка вверх — строить вверх; стрелка вниз — строить вниз)
Достроить название интервалов, определить недостающие ноты
Подписать интервалы между нотами и определить тональность пьесы.
тональность ля мажор
/>
Для качественного и простого усвоения материала воспользуйтесь программами для мобильных телефонов на базе ОС Android:
Следующий урок >>
Тестовое занятие
Ваша заявка принята!
Спасибо за обращение, мы свяжемся с вами в ближайшее время.Заходите в наши аккаунты в социальных сетях
Источник
Соль-фа.рф
Сольфеджио — просто и интересно!
Интервалы от ноты си
Простые интервалы от ноты си:
Прима (ч1), малая секунда (м2), большая секунда (б2), малая терция (м3), большая терция (б3), чистая кварта (ч4), чистая кванта (ч5), малая секста (м6), большая секста (б6), малая септима (м7), большая септима (б7), чистая октава (ч8)
Интервалы, построенные от ноты си вверх:
Интервалы, построенные от ноты си вниз:
Составные интервалы от ноты си:
малая нона (м9), большая нона (б9), малая децима (м10), большая децима (б10), чистая ундецима (ч11), чистая дуодецима (ч12), малая терцдецима (м13), большая терцдецима (б13), малая квартдецима (м14), большая квартдецима (б14)
Источник
Интервалы.
Количество ступеней в интервалах:
1 — прима
2 — секунда
3 — терция
4 — кварта
5 — квинта
6 — секста
7 — септимаЛюбой музыкальный интервал имеет 2 звука. Любые две ноты образуют интервал. Например: «Д о — Ми» . Это интервал, то есть расстояние между звуками. Расстояние можно измерить шагами (это будет приблизительное расстояние) или более точно и правильно — измерениями (сантиметр, метр и так далее). В музыке принято измерять приблизительное расстояние от ноты до ноты не шагами, а ступенями. Для того чтобы очень быстро определить интервал необходимо посчитать сколько ступеней (шагов) в него входит. Например, посчитать расстояние от «До» до «Ми». Сначала « шагами-ступенями » — «Д о» — раз, «Р е» — два, «М и» — три . Мы сделали 3 шага, считаем всё, что проговариваем. Значит это терция. Когда мы учились считать в математике, мы загибали пальчики. Здесь необходимо делать тоже самое, считать на пальчиках. Потренируемся еще раз. Для примера возьмем два звука — «Ми бемоль» и «Ре бемоль». Получился широкий интервал. Сначала посчитаем ступени, не берем во внимание бемоли. Итак, загибаем пальчики и считаем. «Ми», «Фа», «Соль», «Ля», «Си», «До», «Ре». Мы прошли семь ступеней. Значит интервал септима. Это приблизительное определение интервала. Теперь более точное
будем измерять « миллиметрами-сантиметрами «. В музыке это называется полутон (п) и тон (т). Результат посмотрим по таблице, данной ниже.Количество тонов:
ч1 (чистая прима) 0т
м2 (малая секунда) п
б2 (большая секунда) 1т
м3 (малая терция) 1,5т
б3 (большая терция) 2т
ч4 (чистая кварта) 2,5т
ч5 (чистая квинта) 3,5т
м6 (малая секста) 4т
б6 (большая секста) 4,5т
м7 (малая септима) 5т
б7 (большая септима) 5,5т
ч8 (чистая октава) 6тИтак, расстояние «Ми бемоль — Ре бемоль» измерим более точно. (Черные клавиши вы можете называть так, как вам нравится, это не меняет суть. Например, «Фа диез» можно назвать «Соль бемоль»).
ми бемоль-ми — полутон
ми-фа — полутон
фа-фа диез — полутон
фа диез-соль — полутон
соль-соль диез — полутон
соль диез-ля — полутон
ля-ля диез — полутон
ля диез-си — полутон
си-до — полутон
до-ре бемоль — полутонДобрались. Складываем все полутона и получаем 5 тонов, малую септиму. Удобнее сразу считать тонами, так быстрее. Посмотрите, пожалуйста, видеоурок — «Тон. Полутон « .
Если мы посмотрим на таблицу определения количества тонов, то увидим некоторую закономерность. Каждый последующий интервал появляется через полутон. Только между чистой квартой и чистой квинтой — это расстояние 1 тон. Между этими интервалами помещается тритон , т .е. интервал, который содержит три тона.
Для того чтобы быстро и легко выучить таблицу, запомним следующим образом. Для начала выучим чистую октаву, в ней 6 тонов. Затем, рядом стоящие большую и малую септимы, соответственно — 5,5 и 5 тонов. Следующий шаг для запоминания — кварта и квинта. Между ними «живет тритон», следовательно, в чистой кварте на полутон меньше — 2,5т, а в чистой квинте на полутон больше — 3,5т. Далее от чистой квинты запоминаем сексту и, напоследок, секунды и терции.Источник
Обращение интервалов или волшебство на уроках сольфеджио
Обращение интервалов – это превращение одних интервала в другие путём перестановки верхнего и нижнего звука. Как известно, нижний звук интервала называется его основанием, а верхний – вершиной.
И, если, поменять местами вершину и основание, или, другими словами, попросту перевернуть интервал вверх тормашками, то в результате получится новый интервал, который и будет являться обращением первого, исходного музыкального интервала.
Как выполняются обращения интервалов?
Сначала разберём манипуляции только с простыми интервалами. Обращение выполняется путём переноса нижнего звука, то есть основания, на чистую октаву вверх, или перемещением нижнего звука интервала, то есть вершины, на октаву вниз. Результат получится один и тот же. Перемещается только один из звуков, второй звук остаётся на своём месте, его трогать не нужно.
Например, возьмём большую терцию «до-ми» и обратим её любым способом. Сначала, основание «до» перенесём на октаву вверх, у нас получится интервал «ми-до» — малая секста. Затем попробуем поступить наоборот и перенесём вниз на октаву верхний звук «ми», в результате также получаем малую сексту «ми-до». На картинке желтым цветом выделен звук, который остаётся на месте, а сиреневым – тот, который перемещается на октаву.
Ещё пример: дан интервал «ре-ля» (это чистая квинта, так как ступеней между звуками пять, а качественная величина – три с половиной тона). Попробуем сделать обращение этого интервала. Переносим «ре» выше – получаем «ля-ре»; или переносим «ля» ниже и тоже получаем «ля-ре». В обоих случаях чистая квинта обратилась в чистую кварту.
Кстати, путём обратных действий, можно вернуться к исходным интервалам. Так, сексту «ми-до» можно обратить в терцию «до-ми», от которой мы сначала отталкивались, ну а кварту «ля-ре» легко снова превратить в квинту «ре-ля».
О чём это говорит? Это говорит о том, что между разными интервалами есть какая-то связь, и о том, что существуют пары взаимно обращаемых интервалов. Эти интересные наблюдения легли в основу законов интервальных обращений.
Законы обращения интервалов
Мы знаем, что у любого интервала есть два измерения: количественная и качественная величина. Первая выражается в том, сколько ступеней охватывает тот или иной интервал, обозначается числом, и от неё зависит название интервала (прима, секунда, терция и другие). Вторая указывает на то, сколько в интервале тонов или полутонов. И, благодаря ей, у интервалов появляются дополнительные уточняющие названия из слов «чистый», «малый», «большой», «увеличенный» или «уменьшённый». Следует отметить, что оба параметра интервала меняются при обращении – и ступеневый показатель, и тоновый.
Законов-правил всего два.
Правило 1. Чистые интервалы при обращении остаются чистыми, малые превращаются в большие, а большие, наоборот, в малые, уменьшённые делаются увеличенными, ну а увеличенные интервалы, в свою очередь, уменьшёнными.
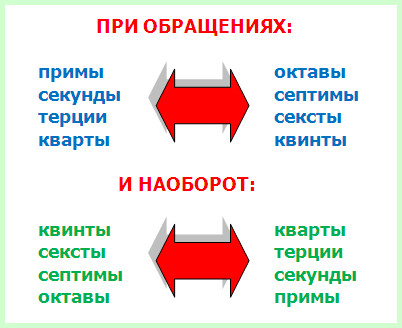
Правило 2. Примы обращаются в октавы, а октавы – в примы; секунды переходят в септимы, а септимы – в секунды; терции становятся секстами, а сексты – терциями, кварты перевоплощаются в квинты, а квинты, соответственно, в кварты.
Сумма обозначений взаимообращающихся простых интервалов равна девяти. Например, прима обозначается числом 1, октава – числом 8. 1+8=9. Секунда – 2, септима – 7, 2+7=9. Терции – 3, сексты – 6, 3+6=9. Кварты – 4, квинты – 5, вместе снова получается 9. И, если вдруг вы забыли, кто куда обращается, то просто из девятки вычитайте числовое обозначение данного вам интервала.
Давайте посмотрим действие этих законов на практике. Даны несколько интервалов: чистая прима от ре, малая терция от ми, большая секунда от до-диеза, уменьшённая септима от фа-диеза, увеличенная кварта от ре. Обратим их и выявим изменения.
Итак, после обращения чистая прима от ре превратилась в чистую октаву: тем самым находят подтверждения два момента: во-первых, чистые интервалы и после обращения остаются чистыми, а, во-вторых, прима стала октавой. Далее, малая терция «ми-соль» после обращения явилась как большая секста «соль-ми», что снова подтверждает уже сформулированные нами законы: малое выросло в большое, терция стала секстой. Следующий пример: большая секунда «до-диез и ре-диез» превратилась в малую септиму из тех же звуков (малое – в большое, секунда – в септиму). Аналогично и в других случаях: уменьшённое становится увеличенным и наоборот.
Проверь себя!
Предлагаем немного потренироваться для лучшего закрепления темы.
ЗАДАНИЕ: Дан ряд интервалов, нужно определить, что это за интервалы, затем мысленно (или письменно, если трудно так сразу) обратить их и сказать, во что они превратятся после обращения.
1) даны интервалы: м.2; ч.4; м.6; б.7; ч.8;
2) после обращения из м.2 получаем б.7; из ч.4 – ч.5; из м.6 – б.3; из б.7 – м.2; из ч.8 – ч.1.
Фокусы с составными интервалами
Составные интервалы тоже могут участвовать в обращении. Напомним, что составными называются интервалы, которые шире октавы, то есть ноны, децимы, ундецимы и другие.
Чтобы получить при обращении из простого интервала составной, нужно переместить одновременно и вершину, и основание. Причём, основание – на октаву вверх, а вершину – на октаву вниз.
Например, возьмём большую терцию «до-ми», переместим основание «до» на октаву выше, а вершину «ми», соответственно, на октаву ниже. В результате такого двойного перемещения у нас получился широкий интервал «ми-до», секста через октаву, или, если быть точнее, малая терцдецима.
Подобным же образом, и другие простые интервалы можно превратить в составные и, наоборот, из составного интервала можно получить простой, если вершину его на октаву опустить, а основание поднять.
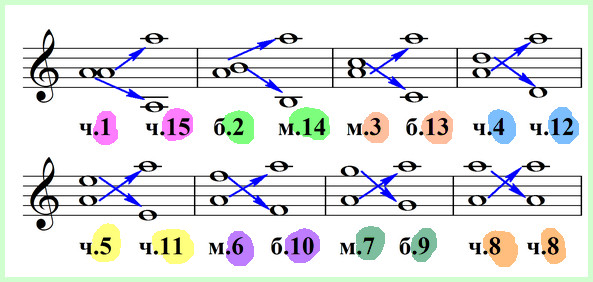
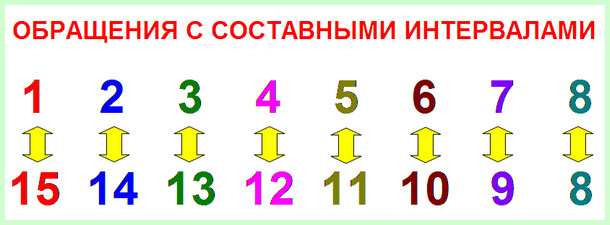
Какие будут соблюдаться закономерности? Сумма обозначений двух взаимообращаемых интервалов будет равна шестнадцати. Так:
- Прима обращается в квинтдециму (1+15=16);
- Секунда превращается в квартдециму (2+14=16);
- Терция переходит в терцдециму (3+13=16);
- Кварта становится дуодецимой (4+12=16);
- Квинта перевоплощается в ундециму (5+11=16);
- Секста оборачивается децимой (6+10=16);
- Септима предстаёт как нона (7+9=16);
- С октавой эти штуки не проходят, она обращается в саму себя и поэтому составные интервалы тут уже не причём, хотя красивые цифры есть и в этом случае (8+8=16).
Применение обращений интервалов
Не стоит думать, что обращения интервалов, так подробно изучаемые в курсе школьного сольфеджио, не имеют никакого практического применения. Напротив, это очень важная и нужная штука.
Практическая область применений обращений связана не только с пониманием того, как возникли некоторые интервалы (да-да, исторически некоторые интервалы были обнаружены путём обращения). Если брать теоретическую область, то обращения очень помогают, например, в запоминании тритонов или характерных интервалов, изучаемых в старших классах и в колледжах, в понимании устройства некоторых аккордов.
Если брать область творческую, то обращения широко применяются при сочинении музыки, причём иногда мы даже их не замечаем. Послушайте, например, кусочек красивой мелодии в романтическом духе, он весь построен на восходящих интонациях терций и секст.
Вы, кстати, тоже легко можете попробовать сочинить нечто подобное. Даже, если взять те же терции и сексты, только в нисходящей интонации:
P.S. Дорогие друзья! На этой ноте мы завершаем сегодняшний выпуск. Если у вас остались ещё вопросы об обращениях интервалов, то, пожалуйста, задайте их в комментариях к этой статье.
P.P.S. Для окончательного усвоения данной темы предлагаем вам посмотреть забавное видео от замечательного учителя сольфеджио наших дней Анны Наумовой.
Источник
- Определить название интервалов


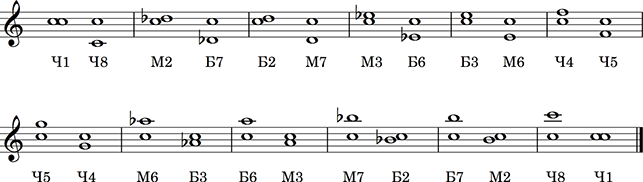














 />
/>