Почему некоторые ноты гармонично звучат вместе
Сохранить и прочитать потом —
Вы никогда не задумывались, почему некоторые ноты больше подходят друг другу, чем другие? Как связаны между собой частоты их волн? Почему ноты одной тональности звучат «хорошо»? Почему «хорошо» звучат ноты в составе аккорда?
Ответ на этот вопрос связан с понятием «консонанса» (т.е. «созвучия») и современной наукой психоакустикой. Консонанс представляет собой согласное, стройное звучание, а диссонанс наоборот – несогласное или беспокойное.
Прежде всего, необходимо различать чистые тона, которые являются обычными синусоидальными волнами, и реальные тона, которые воспроизводятся музыкальными инструментами. Реальные тона, по сути, состоят из гармонических обертонов с разными амплитудами. Таким образом, каждая нота, сыгранная на любом инструменте, представляет собой сложный звук, состоящий из основного тона и большого числа обертонов.
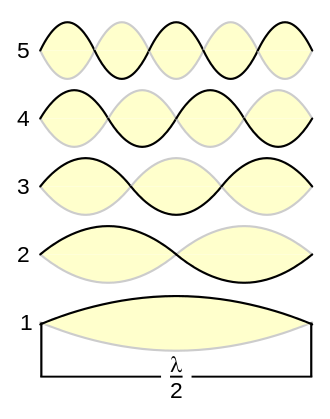
Обертоном называется любая собственная частота выше основной, а те обертоны, частоты которых относятся к частоте основного тона как целые числа, называются гармониками. При этом основной тон считается первой гармоникой. Выходит, что значения частоты каждой гармоники относятся к основному тону следующим образом: f, 2f, 3f, 4f, ….
Частоты гармоник так же относятся друг к другу как целые числа и формируют основные музыкальные интервалы: 2:1 – это октава, 3:2 – это квинта, 4:3 – это кварта и т. д. В разных музыкальных культурах и в разные периоды времени отношение к консонансным и диссонансным интервалам различалось. Во времена Пифагора консонансными интервалами считались октава, квинта и кварта, однако в 13 веке к ним присоединилась терция. Все это связано с изменением музыкальных вкусов.
Иэн Джонстон (Ian Johnston) написал книгу «Measured Tones», в которой описал теорию созвучий (музыкального консонанса). В ней он сравнивает диссонанс с приправами, отмечая тот факт, что все мы относимся к ним по-разному. Строение наших ушей и мозга отличается, потому отличаются и наши понятия о «хорошем звуке».
Лукас Бивальд (Lukas Biewald), основатель компании CrowdFlower, соглашается с тем, что «хорошее звучание» – это очень субъективное понятие. Он говорит, что то, какие песни нам нравятся, зависит от нашей культуры, характера, даже настроения.
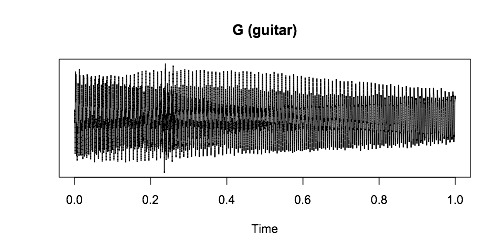
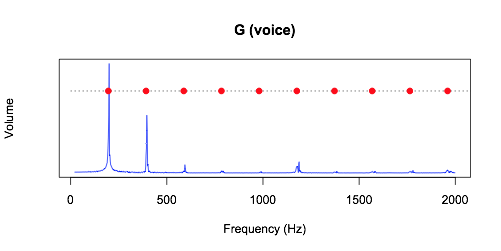
Давайте отойдем от личных предпочтений и немного углубимся в физику происходящих процессов. «Наиболее созвучными будут ноты, имеющие одинаковую высоту тона. Другими словами, соль малой октавы фортепиано созвучна с нотой соль (G) на гитаре, – отмечает Бивальд. – Вот график звуковой волны, которую воспроизводит гитарная струна»:
Звуковая волна – это серия колебаний воздуха, заставляющих вибрировать с разной частотой маленькие волосковые клетки, расположенные во внутреннем ухе человека. Слышимый нами звук являет собой сумму этих вибраций. Чтобы выделить частоты, сокрытые в этом звуке, обратимся за помощью к математике и воспользуемся преобразованием Фурье.
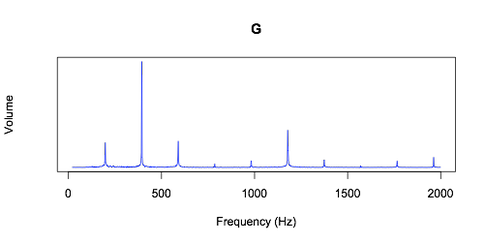
На графике мы видим, что нота соль содержит несколько частот. Самая низкая частота колебания струны равняется 196 Гц. Эта частота называется основной. Но мы видим, что есть частоты, которые превышают её в два и более раз – это обертоны или гармоники.
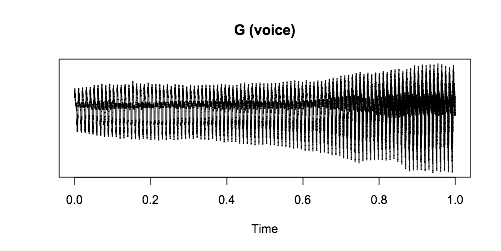
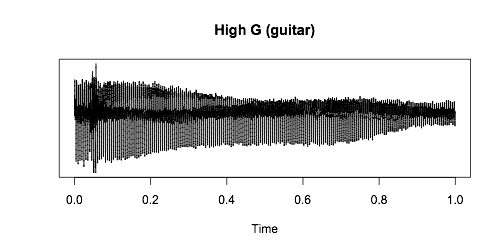
Когда Лукас Бивальд пропел ноту соль, одновременно ударяя по струне G на гитаре, получился уже вот такой график:
Внешний вид кривой отличается, но если сравнить частотные графики, то они совпадут.
Красными точками отмечены частоты гармоник. Между ними ровно 196 Гц, как и в предыдущем случае. Бивальд говорит: «Когда я пою ноту соль и беру её на гитаре, воздушные вибрации, исходящие от голосовых связок и струны инструмента, воздействуют на одни и те же волосковые клетки в моём ухе».
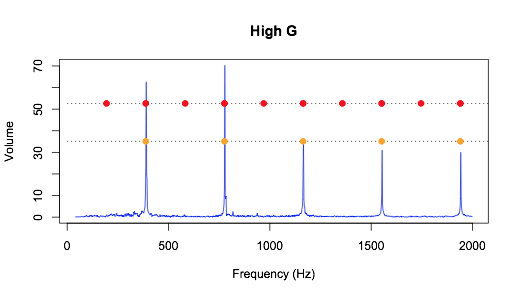
Давайте посмотрим на график, который получится, если сыграть ноту соль на гитаре, но на октаву выше. Он отличается от двух предыдущих.
Если взглянуть на частоты гармоник, то мы заметим, что положение некоторых из них совпадает. Как результат, в обоих случаях будут вибрировать практически одни и те же волосковые клетки уха. Именно поэтому у нас возникает ощущение того, что это две одинаковые ноты, хотя они и отличаются на одну октаву.
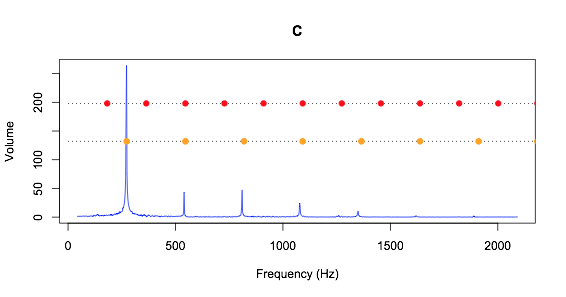
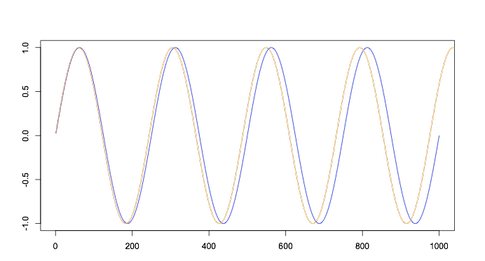
«Помимо понятия октавы у нас еще есть понятие квинты. Две ноты, которые различаются на квинту, наиболее созвучны», – говорит Бивальд. Отношение между нотами до и соль равняется квинте. Поэтому в западной музыкальной традиции большинство аккордов, строящихся от ноты до, содержат в себе ноту соль. Но почему они так подходят друг другу? Вот частоты ноты до, сыгранной на гитаре Бивальда.
Здесь красным отмечены частоты ноты соль, а жёлтым – ноты до. Видно, что они не всегда перекрываются, но поскольку основная частота ноты до относится к основной частоте ноты соль как 3/2, то совпадают каждая третья гармоника соль и каждая вторая гармоника до.
Считается, что нотами, которые наиболее созвучны с до, являются фа и соль, поскольку они находятся на расстоянии идеальной кварты и идеальной квинты соответственно. Давайте взглянем на их гармоники.
Гармоники соль и фа часто перекрывают гармоники до. Однако гармоники соль и фа совпадают на порядок реже. Именно поэтому, когда мы слышим ноты соль+до и фа+до, они кажутся нам консонансными, а когда слышим фа+соль – у нас возникает чувство диссонанса. По этой причине эти три ноты практически никогда не берутся одновременно. Теперь взглянем на более подробный график:
Видно, что у до и ми много совпадающих гармоник, поэтому ноты до, соль и ми образуют аккорд до мажор. У до и ре-диез (ми-бемоль) столько же совпадающих гармоник, поэтому ноты до, ми-бемоль и соль образуют аккорд до минор. Если гармоники нот никак друг с другом не соотносятся, то при одновременном их [нот] воспроизведении мы слышим диссонанс. Например, до и фа-диез – у них нет перекрывающихся гармоник. Подробнее об этом вы можете прочитать в другом ответе Лукаса Бивальда.
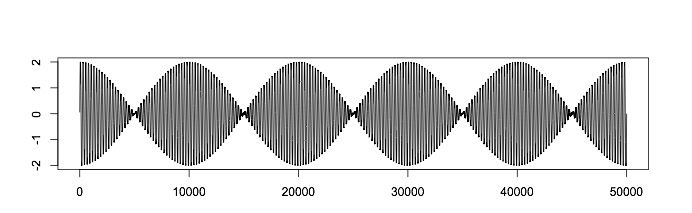
Есть и другие психоакустические эффекты, влияющие на наше восприятие звука. Диссонанс возникает в тот момент, когда мы слышим два звука с практически одинаковыми, но все же различными, частотами.
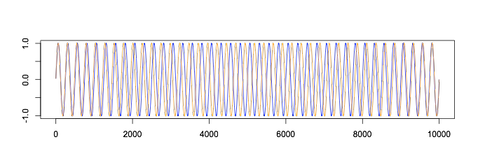
Со временем сдвиг по фазе увеличивается:
Мы с вами слышим сумму голубого и оранжевого сигналов:
Если растянуть временную шкалу, то мы получим:
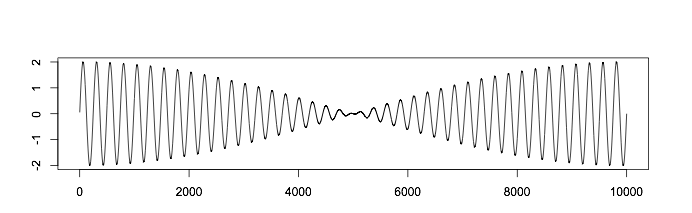
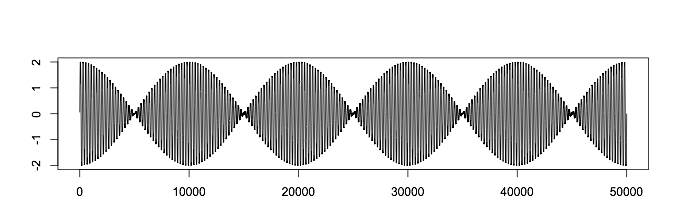
Когда сигналы находятся в фазе, они усиливают друг друга, и возникает усиливающая интерференция. По мере сдвига возникает ослабляющая интерференция, и сигналы начинают гасить друг друга до тех пор, пока не окажутся в строгой противофазе.
Из-за этого возникает пульсирующий звук, который вы наверняка слышали (сыграйте на расстроенной гитаре или фортепиано). Для западного слушателя он покажется диссонансным, но этот прием используется в музыке некоторых культур.
Источник
Как ноты влияют на эмоции — подробности #1
В прошлых двух постах были видосы про то, как, чередуя два аккорда на музыкальном инструменте, вызывать у людей определённые эмоции.
Появилось время, тогда давайте разберём эту тему поподробнее.
Сначала введение в связь созвучий и настроения, а в следующем посте разберём уже сами видео.
Когда мы играем несколько нот одновременно — их звуки (а по-физическому — частоты) для нашего уха смешиваются. То, насколько эти частоты “уживаются” вместе — насколько ноты консонантны — влияет на то, насколько нам приятно их общий звук слушать.
Консонанс — это, дословно, созвучность. Диссонанс — соответственно, наоборот — плохо звучащие вместе звуки. Давайте наглядно посмотрим на разницу.
Так как отдельные ноты — это разные частоты — разные звуковые волны — для экспериментов, мы можем описать их с помощью математической функции.
В реальности, каждая частота создаёт ряд гармоник — частот кратных изначальной (2x, 3x, 4x, …). А инструменты ещё привносят свои обертона (более широкое понятие, включающее в себя гармоники), которые появляются из-за материальности инструментов.
Например, струна колеблется не только по всей длине, но и частями:
Картинка с википедии.
Но для наглядности можно использовать синусоидальную волну в вакууме. И то, как ноты “уживаются” вместе посмотреть на графиках их функций. Дальше я буду использовать термины из моей карточки по интервалам: Помощь с теорией музыки #2
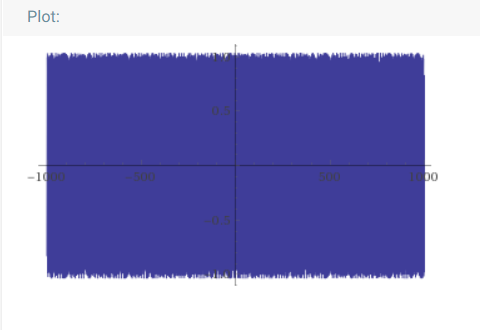
Сначала посмотрим на то, с чем будем сравнивать. График одной ноты:
По-горизонтали — время. Какой конкретно это отрезок времени — для нас не важно. Важно то, что все графики здесь — за одинаковый промежуток времени.
По-вертикали — амплитуда — для нас это громкость звука.
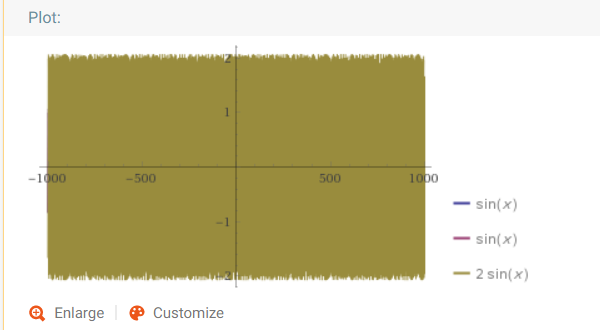
На каждом графике с двумя нотами три линии. Две (синяя и лиловая) — частоты, которые мы складываем, и одна — их сумма (жёлтая). Нам сейчас нужна именно жёлтая. Давайте посмотрим:
“Полный консонанс” — две одинаковые ноты — унисон — звучит приятнее всего:
Обратите внимание на “заполненность” графика по-вертикали. Форма графика полностью повторяет график выше с одной нотой, только с амплитудой вдвое больше.
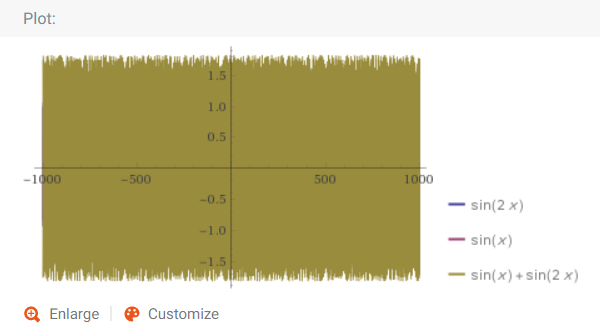
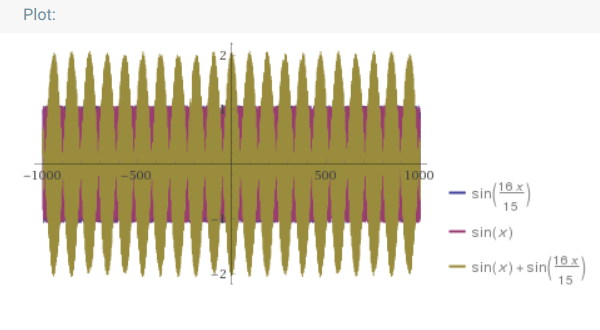
Октава чуть менее приятна, потому что функции не идентичны:
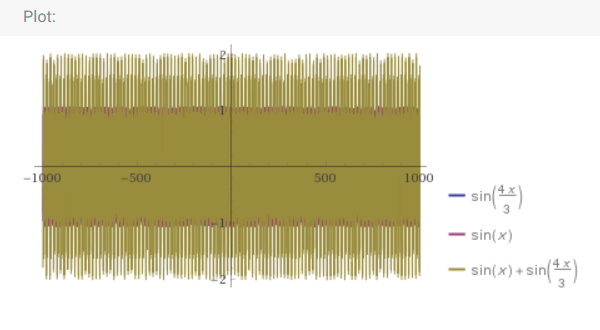
Меньше консонанса (кварта — 5 полутонов между нотами):
Из-за того, что частоты у нот разные — появляется интерференционная картина — наложение двух частот друг на друга усиливают или ослабляют друг друга в определённом закономерном рисунке.
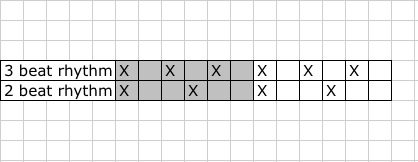
Этот рисунок повторяется, потому что сами частоты тоже периодичны. Это как считать до двух и до трёх:
Наименьшее общее кратное (НОК) этих двух чисел — это сколько шагов будет длиться наша “интерференционная” картина, пока не начнёт повторяться.
На примере 2 и 3:
НОК для 2 и 3 = 6. Это наименьшее число, которое делится на оба числа без остатка.
Первые 12 шагов:
6/3 = 2 — сколько раз повторится первая частота.
6/2 = 3 — сколько раз повторится вторая.
И 6 — это до скольки надо досчитать до повторения.
То же самое можно проделать и с реальными частотами. Чтобы не считать большие числа (стандартная нота ля колеблется 440 раз в секунду), можно эти частоты взаимно сократить. Числа, которые не имеют общих делителей называются “взаимно простые числа”. Чтобы сэкономить время, вот отношения частот:
Октава (1:2), квинта (2:3), кварта (3:4), большая терция (4:5), малая терция (5:6), большая секунда (8:9), малая секунда (9:10), и тритон (15:16).
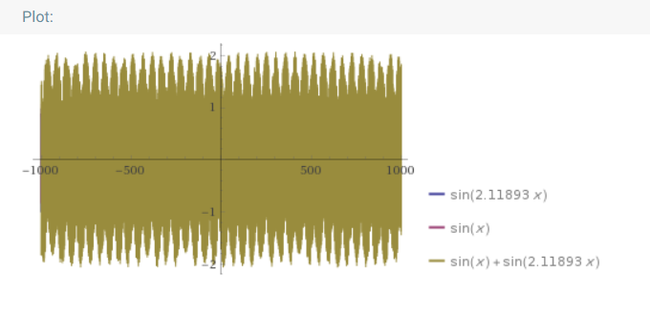
Минимум консонанса (злой и страшный пан тритон, он в диссонансе знает тон):
По графику мы можем увидеть, что перепады громкости звука уже очень сильна, и сам звук нами воспринимается как этакое “дрожание” звука, менее приятное для нас (а в данном случае — это самое неприятное сочетание, если не брать меньше полутона между нотами).
При слишком большой или слишком маленькой разнице между частотами возникает дополнительное “биение” в звуке, которое довольно явно воспринимается нашим ухом (больше тут: https://ru.wikipedia.org/wiki/Биения ).
— В зависимости от того, какие две ноты мы берём — звук будет более или менее приятный для нас.
— “Приятность” звука зависит от отношения частот. Сначала сократим частоты, потом находим наименьшее общее кратное.
— Чем меньше НОК — тем “приятнее” созвучие.
— Чем больше НОК — тем больше будет “дрожание” звука или уже биение.
— Биение на слух воспринимается как “пульсация” звука.
Двух нот не всегда достаточно, поэтому надо уметь расположить не две ноты, а три, да так, чтобы они звучали гармонично, консонантно, приятно и вообще.
Как стабильную основу можно вместе с нотой взять квинту (получить самое приятное и “уместное” созвучие). Тогда добавив новую ноту, уже третью, также, как было описано выше, можно влиять на эмоциональную окраску аккорда (созвучия из трёх звуков = трезвучия = аккорда).
Но это уже совсем другая история.
В следующем посте уже разберём эту другую историю вместе с полезной нагрузкой из видео.
Надеюсь, было интересно!
Бонусом, вот график нот на расстоянии в полторы октавы (нона):
И интервалы от унисона до квинты (в секстах и септимах ничего экзотичного нет, они работают также. Но вот вам ссылка: https://www.wolframalpha.com/input/?i=plot+sin%2816x%2F9%29%. — 16x/9 можно заменить на любое отношение частот из поста или этих ваших интернетов)
По-книжному: Унисон, октава, м. секунда, б. секунда, м. терция, б. терция, кварта, тритон, квинта:
Источник