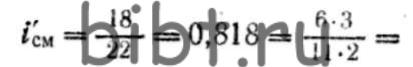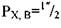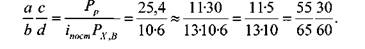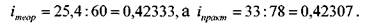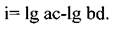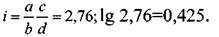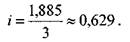§ 3. МЕТОДЫ ПОДБОРА СМЕННЫХ КОЛЕС ГИТАР.
(рис. 2) называется устройство, обеспечивающее правильное сцепление сменных зубчатых колес.
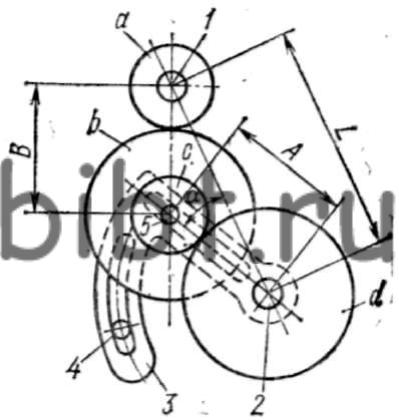
Рис. 2. Схема двухпарной гитары
Расстояние L между ведущим 1 и ведомым 2 валами является неизменным. На ведомом валу свободно установлен приклон гитары 3, закрепленный болтом 4. Ось 5 промежуточных колес b,с можно перемещать по радиальному пазу, тем самым изменяя расстояние А между центрами колес с и d. Дуговой паз позволяет регулировать размер В. Чтобы подобранные сменные зубчатые колеса не упирались во втулки валов 1, 2, необходимо соблюдать условия их сцепляемости:
При подборе колес необходимо учитывать и допускаемые пределы передаточных отношений пар сменных колес 1/5 с+(15-:-20) или 60+70>40+15;
c+d>b+(15-:-20) или 40+80>70+15.
Способ замены часто встречающихся чисел приближенными дробями заключается в том, что часто встречающиеся при нарезании дюймовых резьб, червяков и в других случаях числа π и 25,4 (числовое значение дюйма) заменяют приближенными значениями, удобными для подбора сменных колес, например:
1» ≈ 25,4 мм =127/5 мм; π≈22/7≈(19*21)/127 и т.д.
Полученная при этом погрешность не должна превышать заданной по условию. Абсолютная погрешность наладки
относительная погрешность наладки
где i см — заданное передаточное отношение; i’ см — полученное передаточное отношение сменных колес.
Способ подбора сменных колес на логарифмической линейке наименее точен. Край движка логарифмической линейки устанавливают против числа, соответствующего передаточному отношению гитары сменных колес. Передвижением бегунка находят риски, совпадающие на движке и на линейке. По полученным новым целым числам, которые дают при делении те же значения частного, подбирают числа зубьев сменных зубчатых колес:
и т. д.
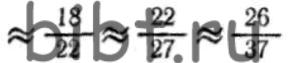
Выбирают наиболее точные и удобные значения i’ см для подбора колес: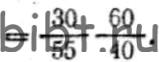
. Затем подсчитывают абсолютную погрешность ∆i= 0,818 — 0,817 = 0,001; относительную погрешность δ=0,001/0,817=0,0012239.
Способ подбора сменных колес по таблицам очень точен, но его следует применять лишь в тех случаях, когда нельзя подобрать колеса методом разложения на сомножители. Наиболее быстрый подбор сменных колес можно выполнить по таблицам, приведенным в работе [22].
Источник
Настройка гитары дифференциала
Мастера, технологи и фрезеровщики механообрабатывающих цехов, в станочных парках которых есть зубофрезерные станки, регулярно сталкиваются при изготовлении косозубых цилиндрических зубчатых колес с вопросом максимально точного подбора шестеренок гитары дифференциала.
Если не вдаваться в подробности работы кинематической схемы зубофрезерного станка и технологического процесса нарезания зубьев червячной фрезой, то данная задача заключается в сборке двухступенчатого цилиндрического зубчатого редуктора с заданным передаточным отношением ( u ) из имеющегося комплекта сменных колес. Этот редуктор и есть гитара дифференциала. В комплект (приложение к станку) входит, как правило, 29 зубчатых колес (иногда более 50) с одинаковым модулем и диаметром посадочного отверстия, но с разным количеством зубьев. В наборе могут присутствовать по две-три шестерни с одинаковым количеством зубьев.
Схема гитары дифференциала изображена ниже на рисунке.
Настройка гитары дифференциала начинается с определения расчетного передаточного отношения ( u ) по формуле:
u = p *sin ( β )/( m * k )
p – параметр конкретной модели станка (число с четырьмя-пятью знаками после запятой).
Значение параметра ( p ) индивидуально для каждой модели, приводится в паспорте на оборудование и зависит от кинематической схемы привода конкретного зубофрезерного станка.
β – угол наклона зубьев нарезаемого колеса.
m – нормальный модуль нарезаемого колеса.
k – число заходов червячной фрезы, выбранной для работы.
После этого необходимо выбрать из набора такие четыре шестерни с числами зубьев Z1 , Z2 , Z3 и Z4 , чтобы, установленные в гитару дифференциала, они образовали редуктор с передаточным отношением ( u’ ) максимально близким к рассчитанному значению ( u ).
Как это сделать?
Подбор чисел зубьев шестеренок, обеспечивающий максимальную точность, можно выполнить четырьмя способами (по крайней мере, известными мне).
Рассмотрим кратко все варианты на примере зубчатого колеса с модулем m =6 и углом наклона зубьев β =8°00’00’’. Параметр станка p =7,95775. Червячная фреза – однозаходная k =1.
Для исключения ошибок при многократных расчетах составим простую программу в Excel, состоящую из одной формулы, для расчета передаточного числа.
Расчетное передаточное число гитары ( u ) считываем
в ячейке D8: =D3*SIN (D6/180*ПИ())/D5/D4 =0,184584124
Относительная погрешность подбора не должна превышать 0,01%!
δ =|( u — u’ )/ u |*100 u ) представляем приближениями в виде обычных дробей.
u =0,184584124≈5/27≈12/65≈79/428≈ 91/493 ≈6813/36910
Это можно сделать при помощи программы для представления многозначных констант приближениями в виде дробей с заданными точностями или в Excel подбором.
Выбираем подходящую по точности дробь и раскладываем ее числитель и знаменатель на произведения простых чисел. Простые числа в математике – это те, что делятся без остатка только на 1 и на себя.
u’ =91/493=0,184584178
91/493=(7*13)/(17*29)
Умножаем числитель и знаменатель выражения на 2 и на 5. Получаем результат.
Вычисляем относительную погрешность выбранного варианта.
δ =|( u — u’ )/ u |*100=|(0,184584124-0,184584178)/0,184584124| *100=0,000029% Z1 =23 Z2 =98 Z3 =70 Z4 =89
u’ =(23*70)/(98*89)=0,184590690
δ =|( u — u’ )/ u |*100=|(0,184584124-0,184590690)/0,184584124| *100=0,003557% Z1 =23 Z2 =89 Z3 =50 Z4 =70
u’ =(23*50)/(89*70)=0,184590690
δ =|( u — u’ )/ u |*100=|(0,184584124-0,184590690)/0,184584124| *100=0,003557% Уважающих труд автора приглашаю подписаться на анонсы статей, чтобы не пропустить появление возможно важной для вас информации (подписные формы — в конце статьи и наверху страницы).
Статьи с близкой тематикой
Отзывы
14 комментариев на «Настройка гитары дифференциала»
- tehotdel.nov 08 мая 2015 15:49
Пользуюсь вот Duncans Gear calculator, но хотелось бы оправославить все это дело в excel’е, т.к. там считаю передаточное — хотелось бы сразу все в одном месте иметь. Ума не приложу какие функции будут перебирать ряд колес (например, от 23 до 100) да еще чтоб дважды не перебирал одно и то же, считать их соотношение. А два числа сравнить то я уж сумею xD
Алгоритм решения этой задачи можно реализовать в Excel (Excel может всё!), но требуется поработать.
Ссылка на блок-схему алгоритма:
Ладно, скрипт так скрипт. Благодарю)
Александр, опираясь на Вашу статью разработал программу «Настройка гитары дифференциала» в VB6. Скачать ее можно на страничке twirpx.com/file/1676547/.
Использую ее в производстве.
Последнюю версию (значение угла можно вводить в формате ГГ.ММСС) могу выслать каждому желающему. (gerasimow1.narod.ru)
Спасибо за полезную информацию, как раз сейчас восстанавливаю себе зубофрезер 5к324. Для начала буду пользоваться Duncans, но на будущее планирую поставить электропривод, управляемый микроконтроллером, так, чтобы в сам микроконтроллер загонять данные колеса и фрезы, а он сам считал нужный коэффициент передачи и осуществлял с этим коэффициентом синхронизацию вращения шпинделя и стола.
Доброго времени . Подскажите где можно скачать программу настройки гитары дефферициала ? для мод 532 , К532А
Если Вы внимательно прочитаете еще раз статью, то сами ответите на свой вопрос.
Для модели 532 p=5,9683.
(p – параметр конкретной модели станка (число с четырьмя-пятью знаками после запятой)
У меня станок 5Е32П, а р я не знаю.Не подскажите?
Не подскажу. Поищите паспорт на свой станок в интернете.
Можете посчитать мне гитара дифференциала для шестерни
p – параметр конкретной модели станка (число с четырьмя-пятью знаками после запятой).
Значение параметра (p) индивидуально для каждой модели, приводится в паспорте на оборудование и зависит от кинематической схемы привода конкретного зубофрезерного станка.
β – угол наклона зубьев нарезаемого колеса.
m – нормальный модуль нарезаемого колеса.
k – число заходов червячной фрезы, выбранной для работы.
Какой набор колес для гитары дифференциала у вас есть в наличии (число зубьев / количество штук в наборе; полный список)?
Материал представляет интерес. Занимаемся вопросом давно. Можете выслать задание на создание набора колёс (минимальное и максимальное количества зубьев колёс набора, количество колёс в наборе, условие сцепляемости, другие требования) — решим. Можете выслать существующий набор — определим характеристики (диапазон реализуемых передаточных отношений и количество отношений, график плотности распределения в диапазоне, другое).
Здравствуйте, Александр! Проблема с настройкой станка 5324 на косозубую шестеню. Вернее, с самой кинематикой. Знаю, что для этого нужно разблокировать дифф-ал кулачковой муфтой. Та, что в паспотре на картинке не совсем понятна. Если я выложу кинематическую схему станка, Вы сможете подсказать, что и с чем нужно блокировать? Спасибо!
Андрей, здравствуйте. Ваш комментарий попал в спам, и я его не увидел. За 10 прошедших дней, думаю, разобрались с кинематикой?
Источник
ПОДБОР ЧИСЕЛ ЗУБЬЕВ СМЕННЫХ ЗУБЧАТЫХ КОЛЕС
У некоторых металлорежущих станков для наладки кинематических цепей применяют устройства, называемые гитарами (см. рисунок 11, г). Они обеспечивают необходимое сцепление сменных зубчатых колес. Для осуществления точных передаточных отношений используют двухпарные и трехпарные гитары. Каждая гитара снабжена определенным набором сменных колес.
Нормальные комплекты сменных зубчатых колес приведены, в таблице 4. Чтобы подобранные сменные зубчатые колеса могли поместиться на гитаре и не упирались во втулки валиков зубчатых колес, необходимо соблюдать следующие условия зацепляемости: а+Ь^Н-( 15-22); с+ё^э+(15-22).
Суммы чисел сопряженных колес не должны превышать допустимого значения, определяемого конструкцией и размерами места, отведенного для размещения гитары на станке.
Существует несколько способов подбора чисел зубьев сменных зубчатых колес.
Способ разложения на простые множителиприменяют в том случае, если на них можно разложить числитель и знаменатель передаточного отношения, полученного по уравнению наладки.
Произведя разложение, сокращают дробь или вводят дополнительные множители, комбинируя их так, чтобы получить выражение дроби через числа зубьев, имеющихся в комплекте сменных колес.
 |
 |
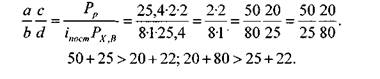Пример 1. Подсчитать сменные зубчатые колеса на нарезание дюймовой резьбы с числом ниток на один дюйм к=8 на токарно-винторезном станке с шагом ходового винтаи постоянным передаточным отношением 1ПОст =1 /2: 
Способ замены часто встречающихся чисел приближенными дробямизаключается в том, что часто встречающиеся числа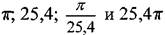 
заменяют
приближенными величинами (таблица 7), дающими возможность с достаточной точностью получить передаточные отношения. Этот метод находит применение на токарно-винторезных станках при необходимости нарезания модульной или пит-чиевой резьбы, а также при нарезании дюймовой резьбы в случае отсутствия в наборе колеса с числом зубьев z=127.
П р и м е р 2. Подобрать сменные зубчатые колеса для нарезания дюймовой резьбы с числом ниток на один дюйм к=10 на токарно-винторезном станке с шагом винта рх, в = 6мм и постоянным передаточным отношением 1Пост = 1-
Решаем этот пример пользуясь таблицей 7:
При применении приближенных способов подбора сменных колес, полученное передаточное отношение отличается от заданного, поэтому возникает необходимость в определении погрешности наладки. Например, в нашем случае
Абсолютная погрешность будет равна 0,42333-0,42307=0,00026
 |
Логарифмический способоснован на том, что находят логарифм передаточного отношения (если передаточное отношение имеет вид неправильной дроби, берут логарифм величины, обратной передаточному отношению) и по соответствующей таблице В. А. Шишкова определяют числа зубьев сменных зубчатых колес.
Этот способ основан на принципе логарифмирования передаточного отношения и дает зубчатые колеса пяткового набора с весьма малой ошибкой. Передаточное отношение зубчатых колес гитары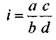 
после логарифмирования имеет вид lg
| Таблица 8 |
Например, для передаточного отношения 
В соответствующей колонке таблиц В.А. Шишкова (см. таблицу 8) находим близкое значение логарифма lg i, которому соответствуют сменные зубчатые колеса гитары с передаточным отношением
В таблице 6 даны значения передаточных отношений меньше единицы, поэтому для i>l нужно брать логарифм обратной! величины передаточного отношения:
 |
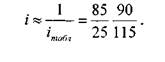Подбор чисел зубьев колес по логарифмической линейке.Край движка логарифмической линейки устанавливают против числа, соответствующего передаточному отношению. Передвижением визира находят риски, совпадающие на движке и на линейке. Риски должны соответствовать целым числам, которые дают при делении значение передаточного отношения. Затем подбирают числа зубьев сменных зубчатых колес, например, способом разложения на простые множители:
Оставив движок в полученном положении, передвигаем визир до тех пор, пока риски на движке и на линейке не совпадут. Тогда
Этот способ подбора колес при нарезании резьб применять, как правило нельзя, так как его точность обычно невысока.
Подбор чисел зубьев по таблицам М.В. Сандакова.Очень часто передаточное отношение содержит дробные числители и знаменатели или множители, некратные набору колес. В этом случае удобно подбирать числа зубьев зубчатых колес по таблицам М.В. Сандакова, содержащим 100 000 передаточных отношений. Заданное передаточное отношение в виде простой правильной дроби, неудобное для преобразования, нужно прежде всего обратить в десятичную дробь с шестью знаками после запятой. Если дробь неправильная, то необходимо разделить ее знаменатель на числитель, чтобы получить десятичную дробь меньше единицы. После этого в таблице находят десятичную дробь, равную полученной или ближайшую к ней, а рядом — соответствующую ей простую дробь. Получив простую дробь, далее
числа зубьев сменных колес подбирают обычным способом, например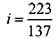 
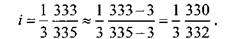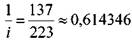
, от-
 |
Получили дробь, легко разлагающуюся на сомножители. Теперь, пользуясь ранее рассмотренным способом, подберем зубчатые колеса:
Подобранныеколеса имеются в наборе для затыловочных станков. Способ Кнаппе.Этот способ основан на том, что к числителю и знаменателю дробей, близких к единице, можно прибавлять (или вычитать) равное число единиц без существенного изменения величины дроби.  Пусть 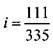 . Разделив эту дробь, получим « -. Тогда можно записать Получили множитель в виде дроби 333 /ззз> близкой к 1. Пользуясь сформулированным выше правилом, можно записать  куда. Из таблицы М.В. Сандакова имеем 0,614346 Ввиду того, что у передаточного отношения перед обращением в десятичную дробь числитель и знаменатель поменять местами, у приближенного числа делают то же самое. Тогда |
Этот метод рекомендуется применять при отсутствии таблиц, специально предназначенных для подбора сменных колес. Он удобен также для подбора трех-парных гитар.
Источник