Преобразование интервалов от ноты ми

Соль-фа.рф

Сольфеджио — просто и интересно!

Интервалы от ноты ми

Простые интервалы от ноты ми:

Прима (ч1), малая секунда (м2), большая секунда (б2), малая терция (м3), большая терция (б3), чистая кварта (ч4), чистая кванта (ч5), малая секста (м6), большая секста (б6), малая септима (м7), большая септима (б7), чистая октава (ч8)

Интервалы, построенные от ноты ми вверх:

Интервалы, построенные от ноты ми вниз:

Составные интервалы от ноты ми:

малая нона (м9), большая нона (б9), малая децима (м10), большая децима (б10), чистая ундецима (ч11), чистая дуодецима (ч12), малая терцдецима (м13), большая терцдецима (б13), малая квартдецима (м14), большая квартдецима (б14)

Источник

Все интервалы от ми вверх и вниз

Ответ или решение 2

Построение интервалов от ноты ми вверх:

чистая прима – ми-ми;

малая секунда – ми-фа; большая секунда – ми-фа диез;

малая терция – ми-соль; большая терция – ми-соль диез;

чистая кварта – ми-ля; увеличенная кварта – ми-ля диез;

уменьшенная квинта – ми-си бемоль; чистая квинта – ми-си;

малая секста – ми-до; большая секста – ми-до диез;

малая септима – ми-ре; большая септима – ми-ре диез;

чистая октава – ми-ми через октаву вверх.

Построение интервалов от ноты ми вниз:

чистая прима – ми-ми;

малая секунда – ми-ре диез; большая секунда – ми-ре;

малая терция – ми-до диез; большая секунда – ми-до;

чистая кварта – ми-си; увеличенная кварта – ми-си бемоль;

уменьшенная квинта – ми-ля диез; чистая квинта – ми-ля;

малая секста – ми-соль диез; большая секста – ми-соль;

малая септима – ми-фа диез; большая септима – ми-фа;

Источник

Обращение интервалов или волшебство на уроках сольфеджио

Обращение интервалов – это превращение одних интервала в другие путём перестановки верхнего и нижнего звука. Как известно, нижний звук интервала называется его основанием, а верхний – вершиной.

И, если, поменять местами вершину и основание, или, другими словами, попросту перевернуть интервал вверх тормашками, то в результате получится новый интервал, который и будет являться обращением первого, исходного музыкального интервала.

Как выполняются обращения интервалов?

Сначала разберём манипуляции только с простыми интервалами. Обращение выполняется путём переноса нижнего звука, то есть основания, на чистую октаву вверх, или перемещением нижнего звука интервала, то есть вершины, на октаву вниз. Результат получится один и тот же. Перемещается только один из звуков, второй звук остаётся на своём месте, его трогать не нужно.

Например, возьмём большую терцию «до-ми» и обратим её любым способом. Сначала, основание «до» перенесём на октаву вверх, у нас получится интервал «ми-до» — малая секста. Затем попробуем поступить наоборот и перенесём вниз на октаву верхний звук «ми», в результате также получаем малую сексту «ми-до». На картинке желтым цветом выделен звук, который остаётся на месте, а сиреневым – тот, который перемещается на октаву.

Ещё пример: дан интервал «ре-ля» (это чистая квинта, так как ступеней между звуками пять, а качественная величина – три с половиной тона). Попробуем сделать обращение этого интервала. Переносим «ре» выше – получаем «ля-ре»; или переносим «ля» ниже и тоже получаем «ля-ре». В обоих случаях чистая квинта обратилась в чистую кварту.

Кстати, путём обратных действий, можно вернуться к исходным интервалам. Так, сексту «ми-до» можно обратить в терцию «до-ми», от которой мы сначала отталкивались, ну а кварту «ля-ре» легко снова превратить в квинту «ре-ля».

О чём это говорит? Это говорит о том, что между разными интервалами есть какая-то связь, и о том, что существуют пары взаимно обращаемых интервалов. Эти интересные наблюдения легли в основу законов интервальных обращений.

Законы обращения интервалов

Мы знаем, что у любого интервала есть два измерения: количественная и качественная величина. Первая выражается в том, сколько ступеней охватывает тот или иной интервал, обозначается числом, и от неё зависит название интервала (прима, секунда, терция и другие). Вторая указывает на то, сколько в интервале тонов или полутонов. И, благодаря ей, у интервалов появляются дополнительные уточняющие названия из слов «чистый», «малый», «большой», «увеличенный» или «уменьшённый». Следует отметить, что оба параметра интервала меняются при обращении – и ступеневый показатель, и тоновый.

Законов-правил всего два.

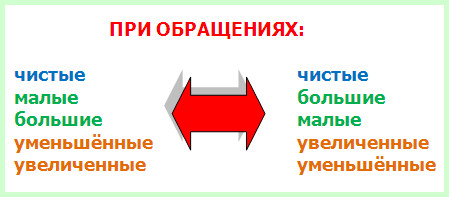
Правило 1. Чистые интервалы при обращении остаются чистыми, малые превращаются в большие, а большие, наоборот, в малые, уменьшённые делаются увеличенными, ну а увеличенные интервалы, в свою очередь, уменьшёнными.

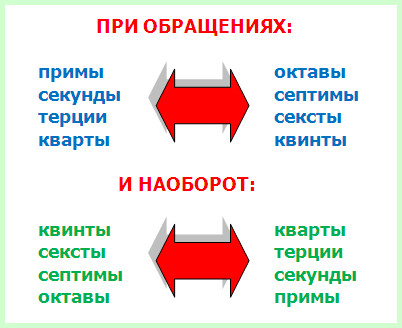
Правило 2. Примы обращаются в октавы, а октавы – в примы; секунды переходят в септимы, а септимы – в секунды; терции становятся секстами, а сексты – терциями, кварты перевоплощаются в квинты, а квинты, соответственно, в кварты.

Сумма обозначений взаимообращающихся простых интервалов равна девяти. Например, прима обозначается числом 1, октава – числом 8. 1+8=9. Секунда – 2, септима – 7, 2+7=9. Терции – 3, сексты – 6, 3+6=9. Кварты – 4, квинты – 5, вместе снова получается 9. И, если вдруг вы забыли, кто куда обращается, то просто из девятки вычитайте числовое обозначение данного вам интервала.

Давайте посмотрим действие этих законов на практике. Даны несколько интервалов: чистая прима от ре, малая терция от ми, большая секунда от до-диеза, уменьшённая септима от фа-диеза, увеличенная кварта от ре. Обратим их и выявим изменения.

Итак, после обращения чистая прима от ре превратилась в чистую октаву: тем самым находят подтверждения два момента: во-первых, чистые интервалы и после обращения остаются чистыми, а, во-вторых, прима стала октавой. Далее, малая терция «ми-соль» после обращения явилась как большая секста «соль-ми», что снова подтверждает уже сформулированные нами законы: малое выросло в большое, терция стала секстой. Следующий пример: большая секунда «до-диез и ре-диез» превратилась в малую септиму из тех же звуков (малое – в большое, секунда – в септиму). Аналогично и в других случаях: уменьшённое становится увеличенным и наоборот.

Проверь себя!

Предлагаем немного потренироваться для лучшего закрепления темы.

ЗАДАНИЕ: Дан ряд интервалов, нужно определить, что это за интервалы, затем мысленно (или письменно, если трудно так сразу) обратить их и сказать, во что они превратятся после обращения.

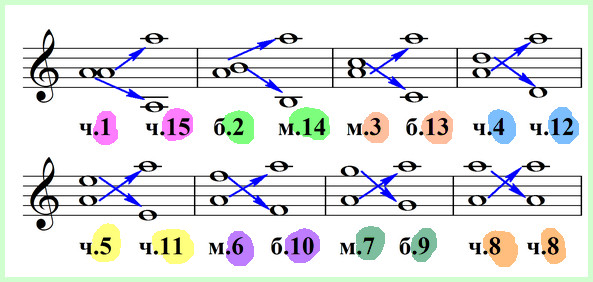
1) даны интервалы: м.2; ч.4; м.6; б.7; ч.8;

2) после обращения из м.2 получаем б.7; из ч.4 – ч.5; из м.6 – б.3; из б.7 – м.2; из ч.8 – ч.1.

Фокусы с составными интервалами

Составные интервалы тоже могут участвовать в обращении. Напомним, что составными называются интервалы, которые шире октавы, то есть ноны, децимы, ундецимы и другие.

Чтобы получить при обращении из простого интервала составной, нужно переместить одновременно и вершину, и основание. Причём, основание – на октаву вверх, а вершину – на октаву вниз.

Например, возьмём большую терцию «до-ми», переместим основание «до» на октаву выше, а вершину «ми», соответственно, на октаву ниже. В результате такого двойного перемещения у нас получился широкий интервал «ми-до», секста через октаву, или, если быть точнее, малая терцдецима.

Подобным же образом, и другие простые интервалы можно превратить в составные и, наоборот, из составного интервала можно получить простой, если вершину его на октаву опустить, а основание поднять.

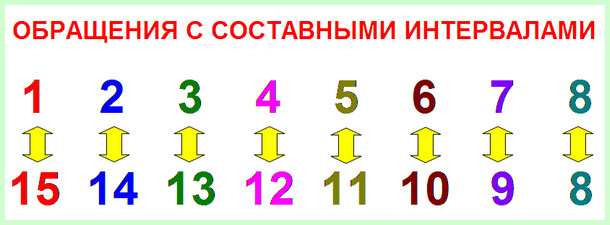
Какие будут соблюдаться закономерности? Сумма обозначений двух взаимообращаемых интервалов будет равна шестнадцати. Так:

• Прима обращается в квинтдециму (1+15=16);
• Секунда превращается в квартдециму (2+14=16);
• Терция переходит в терцдециму (3+13=16);
• Кварта становится дуодецимой (4+12=16);
• Квинта перевоплощается в ундециму (5+11=16);
• Секста оборачивается децимой (6+10=16);
• Септима предстаёт как нона (7+9=16);
• С октавой эти штуки не проходят, она обращается в саму себя и поэтому составные интервалы тут уже не причём, хотя красивые цифры есть и в этом случае (8+8=16).

Применение обращений интервалов

Не стоит думать, что обращения интервалов, так подробно изучаемые в курсе школьного сольфеджио, не имеют никакого практического применения. Напротив, это очень важная и нужная штука.

Практическая область применений обращений связана не только с пониманием того, как возникли некоторые интервалы (да-да, исторически некоторые интервалы были обнаружены путём обращения). Если брать теоретическую область, то обращения очень помогают, например, в запоминании тритонов или характерных интервалов, изучаемых в старших классах и в колледжах, в понимании устройства некоторых аккордов.

Если брать область творческую, то обращения широко применяются при сочинении музыки, причём иногда мы даже их не замечаем. Послушайте, например, кусочек красивой мелодии в романтическом духе, он весь построен на восходящих интонациях терций и секст.

Вы, кстати, тоже легко можете попробовать сочинить нечто подобное. Даже, если взять те же терции и сексты, только в нисходящей интонации:

P.S. Дорогие друзья! На этой ноте мы завершаем сегодняшний выпуск. Если у вас остались ещё вопросы об обращениях интервалов, то, пожалуйста, задайте их в комментариях к этой статье.

P.P.S. Для окончательного усвоения данной темы предлагаем вам посмотреть забавное видео от замечательного учителя сольфеджио наших дней Анны Наумовой.

Источник

Музыкальные интервалы: какие они бывают и как их строить?

Интервалы в музыке – это расстояние между двумя звуками, и еще это созвучие двух нот. Вот такое простое определение можно дать этому понятию. На уроках сольфеджио интервалы поют и слушают, чтобы потом узнавать их в музыкальных произведениях, но сначала нужно научиться строить их от разных нот.

Простых интервалов всего восемь штук, они обозначаются обычными цифрами от 1 до 8, а называются особыми латинскими словами:

1 – прима
2 – секунда
3 – терция
4 – кварта
5 – квинта
6 – секста
7 – септима
8 – октава

Что означают эти названия? В переводе с латинского языка прима – первый, секунда – второй, терция – третий и т.д.

Интересные факты про названия интервалов

Многие из названий интервалов вам уже, наверное, не раз приходилось слышать, даже если разговор не касался музыки. Например, слово «прима» есть в словосочетании «примадонна» (так называют первую, то есть главную артистку-певицу театра).

Слово «секунда» очень напоминает английское числительное «second» (то есть второй), а название шестого интервала «секста» похоже на английское «six» (шесть).

Интересными с этой точки зрения являются интервалы «септима» и «октава» . Помните, как по-английски сказать «сентябрь» и «октябрь»? Это «September» и «October» ! То есть эти названия месяцев имеют те же корни, что и названия интервалов. «Но ведь септима – это семь, а октава – восемь, а указанные месяцы по счету в году девятый и десятый», – скажете вы, и будете совершенно правы. Дело в том, что были времена, когда каждый новый год отсчитывали не от января, как сейчас, а от марта – первого весеннего месяца. Если посчитать так, то все становится на свои места: сентябрь будет седьмым месяцем, а октябрь – восьмым.

Мы еще не сказали ни слова о кварте и терции. С терцией все понятно – ее просто нужно запомнить, но особо наблюдательные, вероятно, заметят, что если прочитать слово «терция» , пропуская каждую вторую букву, то получится обыкновенное «три» .

В русском языке есть слова, похожие на «кварту» : это, например, квартира или квартал. Что такое «квартал» ? Это слово имеет два значения: 1) деление года на 4 равных части; 2) участок городской застройки, который с четырех сторон окружен улицами. Так или иначе здесь фигурирует число 4, и, если запомнить эту ассоциацию, то кварту ни за что не перепутаешь с каким-нибудь другим интервалом.

Как строить интервалы от разных нот вверх и вниз?

Интервалы состоят из двух нот, которые могут быть расположены близко или далеко по отношению друг к другу. И о том, на каком расстоянии они находятся, нам говорит число интервала, которым оно обозначено (от 1 до 8).

Вы знаете, что каждый звук в музыке – это ступень большой музыкальной лестницы. Так вот число интервала показывает, сколько нужно пройти ступенек, чтобы от первого звука интервала добраться до второго. Чем больше число, тем шире интервал, и тем дальше его звуки друг от друга находятся.

Обратимся к конкретным интервалам:

Прима – обозначается числом 1, что говорит нам: два звука находятся на одной и той же ступени . Значит, прима – это обыкновенное повторение звука, шаг на месте: до и еще раз до, или ре и ре, ми-ми и т.д.

Секунда – обозначается двойкой, потому что этот интервал охватывает уже две ступени: один звук находится на какой-либо ноте, а второй на соседней, то есть второй по счету ступени. Например: до и ре, ре и ми, ми и фа и т.д.

Терция – охватывает три ступени. Второй звук находится по отношению к первому на расстоянии трех ступеней, если идти подряд по музыкальной лестнице. Примеры терций: до и ми, ре и фа, ми и соль и т.д.

Кварта – теперь интервал расширяется до четырех ступеней, то есть первый звук находится на первой ступени, а второй звук – на четвертной. Например: до и фа, ре и соль и т.д. Поясним еще раз, что считать ступеньки можно начинать от любой ноты : хоть от до, хоть от ре – выбираем то, что нам нужно.

Квинта – обозначение числом 5 говорит о том, что ширина интервала – 5 ступеней. Например: до и соль, ре и ля, ми и си и т.д.

Секста и септима – числа 6 и 7, которыми они обозначаются, указывают на то, что нужно отсчитать шесть или семь ступеней, чтобы получить сексту или септиму. Примеры секст: до и ля, ре и си, ми и до. Примеры септим (все вверх по лестнице): до и си, ре и до, ми и ре.

Октава – последний интервал, такой же легкий, как и прима. Это тоже повторение звука, только на другой высоте. Например: до первой октавы и до второй октавы, ре и ре, ми и ми и т.д.

А теперь давайте выстроим все интервалы по порядку от ноты ДО и ноты, например, СОЛЬ. Примеры можно послушать. Сделайте это!

Интервалы от ноты ДО вверх

Интервалы от ноты СОЛЬ вверх

ВАЖНО! Считать ступеньки и строить интервалы можно не только вверх, но и вниз . Посмотрите на рисунок: здесь все восемь интервалов построены вниз от нот ДО и ЛЯ.

Интервалы от ноты ДО вниз

Интервалы от ноты ЛЯ вниз

Упражнения : играем интервалы на фортепиано

При изучении интервалов одинаково полезны и взрослым, и детям упражнения на фортепиано или на нарисованной клавиатуре. Фортепиано или синтезатор со звуком, конечно, лучше, потому что цель изучения интервалов на сольфеджио – запомнить не название интервала, не ноты, которые его составляют (хотя это тоже важно), а звучание.

Поэтому если нет подходящего инструмента под рукой, то можно воспользоваться виртуальной клавиатурой или приложением «Пианино» на телефоне (планшете). Важно, чтобы вы работали не в немом режиме, а со звуком (желательно).

Упражнение 1. Играем примы

Примы играть легко, ведь прима – это повторение одной и той же ноты два раза. Значит, нужно просто два раза ударить по любой клавише и уже получится интервал. Прима – очень важный интервал, который встречается во многих песнях, поэтому никогда не нужно забывать о нем (забывают обычно потому, что он легкий).

Упражнение 2. Играем секунды

Секунду всегда образуют две соседние ступени, две ноты, которые находятся рядом. И на клавиатуре пианино, чтобы сыграть секунду, тоже нужно взять две соседние клавиши. Играйте секунды от разных нот – вверх и вниз, запоминайте звучание, можете также параллельно заниматься сольфеджио, то есть пропевать ноты, которые играете.

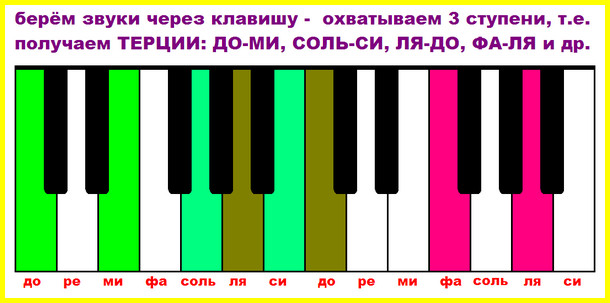
Упражнение 3. Играем терции

Терция – любимый интервал маленького В.А. Моцарта – гения мировой музыки. Известно, что в детстве Моцарт-малыш подходил к клавесину отца (инструмент – предшественник фортепиано), клавиши он не видел (по росту), но дотягивался до них ручками. Моцарт играл всякие созвучия, но больше всего радовался, когда ему удавалось «поймать» терцию – так красиво и мелодично звучит этот интервал.

Попробуйте поиграть терции и вы. Возьмите терцию «ДО-МИ» и запомните это расстояние: звуки расположены на клавиатуре через одну клавишу (через одну ступеньку). Играйте терции вверх и вниз от разных нот. Играйте звуки терций одновременно или поочередно, то есть вразбивку.

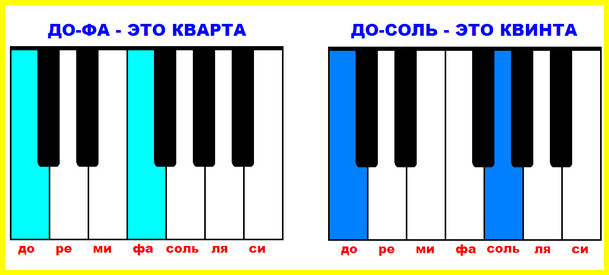
Упражнение 4. Играем кварты и квинты

Кварты и квинты – это интервалы, которые звучат воинственно, призывно и очень торжественно. Недаром с кварты начинается наш российский гимн. Возьмите кварту «ДО-ФА» и квинту «ДО-СОЛЬ», сравните их по звучанию, запомните расстояние. Играйте кварты и квинты от разных нот. Постарайтесь научиться мгновенно находить эти интервалы глазами на клавиатуре.

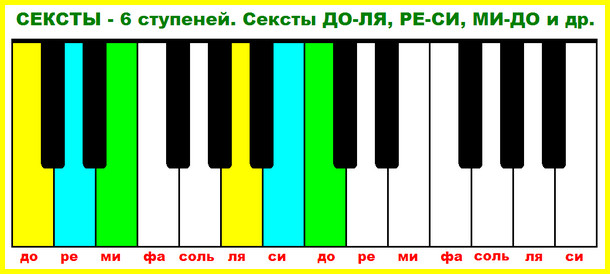
Упражнение 5. Играем сексты

Сексты, как и терции, тоже очень мелодичные и красивые по звучанию. Чтобы быстро сыграть сексту можно мысленно представить себе квинту (ее число 5) и добавить к ней еще одну ступеньку (чтобы было 6). Сыграйте сексты вверх «ДО-ЛЯ», «РЕ-СИ» и от всех других нот и вниз «ДО-МИ», «РЕ-ФА» и т.д.

Упражнение 6. Играем октавы

Октава – это повторение звука в следующей октаве. Вот такое вот парадоксальное и смешное определение можно дать этому интервалу. Найдите на клавиатуре две одинаковых ноты, которые расположены максимально близко: две ДО (одна в первой октаве, вторая – во второй), или две РЕ. Это и будут октавы. То есть октава – это расстояние от одного звука до его повторения музыкальной лестнице. Октавы нужно видеть сразу. Потренируйтесь.

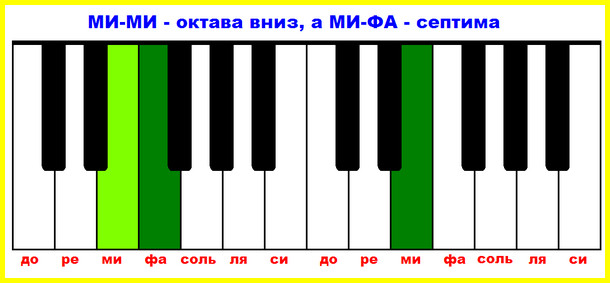
Упражнение 7. Играем септимы

Чуть не пропустили седьмой интервал – септиму. Хотим поделиться с вами одной хитростью. Известно, что число октавы – 8, а септимы – 7. Значит, чтобы получить септиму, нужно всего-то вычесть одну ступеньку из октавы. Это способ быстрого построения септимы, чтобы не считать каждый раз семь ступеней «от печки».

Например: нам нужна септима от РЕ. Представим себе октаву – РЕ-РЕ, а теперь спустим верхний звук на одну ступеньку: получаем септиму РЕ-ДО!

Еще пример: построим септиму от МИ вниз. Отложили вниз октаву – МИ-МИ, а теперь, внимание, нижний звук поднимем на ступень вверх и получим септиму МИ-ФА вниз. А почему мы поднимали нижний звук, а не опускали? Потому что интервалы, построенные вниз, это как отражение в зеркале, и все действия потому нужно делать наоборот.

Дорогие друзья, если вы выполнили предлагаемые упражнения, то вы просто молодцы! Вы многое постигли, но это только начало, первое знакомство с интервалами. Интервалы в таком виде обычно проходят в 1-2 классах музыкальных школ, а потом все становится немного сложнее. И мы приглашаем вас отправиться за новыми знаниями вместе с нами.

В следующих выпусках вы узнаете, о том, что такое количественная и качественная величина интервала, что такое обращения и как можно получить уменьшенные и увеличенные интервалы. До новых встреч!

Источник