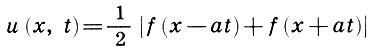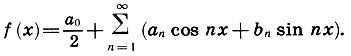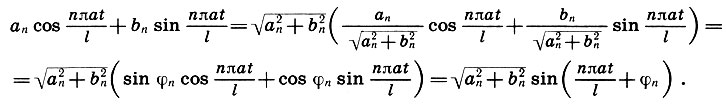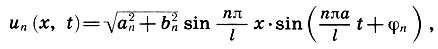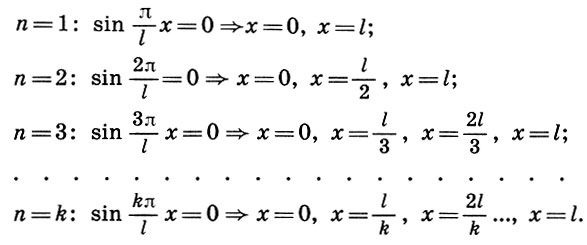Примеры вынужденных колебаний гитара

Примеры вынужденных колебаний гитара

Проблематика проекта:

Изучить физику гитары

Актуальность проблемы:

Использование законов физики для грамотного сочинения мелодий на гитаре

Задачи проекта:

Научиться работать с устройством LabQuest, используя программное обеспечение Logger Pro, для получения графиков колебаний с последующим анализом

Изучить физику звуковых колебаний и стоячих волн

Определить практическое применение полученных знаний

Цель проекта:

1) Изучить физику гитары.

2) Исследовать характеристики звука с помощью графиков, полученных в программе Logger Pro.

3)Исследовать условия возникновения стоячей механической волны.

Использование литературных материалов и степень изученности данного вопроса:

С помощью элементарного учебника физики под редакцией академика Г.С.Ландсберга и учебника «Курс физики» Б.М.Яворского и А.А.Детлафа удалось систематизировать приобретенные знания, составить план, по которому выполнялась исследовательская работа. Изначально степень изученности данной работы была недостаточной для отчетливого представления о проблематике темы. Но благодаря ознакомлению со специальной литературой и интернет-источниками, были выделены и исследованы основные положения работы. Все измерения и полученные по ним графики были выполнены мною самостоятельно.

Для исследования я использовала оборудование:

1) Микрофон 2) LabQuest 3) Программа Logger Pro 4) Электронный усилитель мощности 5) Набор аксессуаров для усилителя мощности 6) Камертоны

Основные этапы работы:

1) Выбор темы работы и обоснование этого выбора 2) Разбор теории работы 3) Проведение исследований 4) Оформление работы. Подготовка презентации для представления проекта

Представление исследовательской работы на городской научно-практической конференции школьников «Физика вокруг нас»

1 этап.Исследование характеристик звука. 5

2 этап.Создание стоячей механической волны. 8

3 этап.О струнах 10

4 этап.Ноты, созвучия и аккорды. 12

5 этап.Акустический резонатор. 13

6 этап.Рассмотрим подробнее устройство гитары. 14

Используемая литература15

Гитара – притягательный инструмент для людей разных поколений, разных возрастов, разных вкусов. Есть народы, испытывающие особое пристрастие к гитаре, например, испанцы. Эту любовь к гитаре, тонкое понимание ее многогранного и богатого звучания ярко выразил известный испанский поэт Федерико Гарсиа Лорка, Например, в своем известном стихотворении «Гитара»:

Тебе не первой, тебе не первой предъявлен веком нелёгкий счёт. Моя гитара, мой спутник верный, давай хоть дождь смахну со щёк.

В России распространение игры на гитаре было связано со становлением традиции городского романса. Во второй половине ХХ века гитарная традиция была оживлена и развита направлением авторской песни, когда поэты сочиняли текст, потом музыку к нему и сами исполняли песню под гитару. Неповторимым талантом исполнения отличались особенно два русских поэта: Булат Окуджава и Владимир Высоцкий. Гитара звучала и неизменно звучит на фестивалях авторской песни. Например, несколько лет подряд такой фестиваль авторской песни проходит под Коломной, в лесу, у станции Пески, куда приезжают и уже признанные поэты, и молодые, дебютные исполнители. Именно гитара, сопровождающая поэтическое слово, создает особую атмосферу теплоты, сердечности, дружеского настроения.

Гитара тот инструмент, который не сразу, но постепенно привлек меня, и я начала учиться игре на гитаре, которая сформировала у меня особое отношение к инструменту, в том числе к его физике.

Итак, что такое звук? Звук- это колебательное движение частиц упругой среды, распространяющееся в виде волн в газообразной, жидкой или твердой сферах.

Как возникает звук? Вблизи источника звука возникают сжатие и разрежение воздуха, то есть колебания давления. Возмущение передается от точки к точке, в пространстве распространяется акустическая волна. Она является продольной в газах и жидкостях. Если частота колебаний лежит в диапазоне 16-20000 Гц, мы слышим звук. Мы различаем разные звуки. Чем же они отличаются?

1 этап. Исследование характеристик звука.

Рассмотрим характеристики звука.

Громкость звука — субъективное качество слухового ощущения, позволяющее располагать все звуки по шкале от тихих до громких. Так как звук переносит изменения давления воздуха, можно предположить, что громкость звука связана с амплитудой колебаний давления.

Громкость звучащего камертона постепенно уменьшается. Почему?Если провести по закопченному стеклу иглой, прикрепленной к звучащему камертону, мы увидим, что амплитуда колебаний уменьшается.

Исследуем звук с помощью микрофона и компьютерной программы Logger Pro:

1) Соберем оборудование следующим образом: к LabQuest присоединим провод для подключения к компьютеру и микрофон, затем подключим LabQuest к розетке и откроем программу Logger Pro.

2) Ударим по камертону слабо, держа возле него микрофон, и запишем данные в компьютерной программе, в результате чего получим график данных колебаний.

3) Затемударим по камертону сильнее, тем самым увеличив амплитуду его колебаний, мы услышим более громкий звук. Получим график аналогичным образом.

Вывод: Второй график отличается от первого большим «размахом», т.е. большей амплитудой колебаний. Следовательно, громкость звука определяется амплитудой колебаний тела.

Вторая характеристика звука — высота.

Возьмем 2 камертона и ударим по ним молоточком,

мы слышим разный звук. Сравним графики этих колебаний

колебания камертона с частотой 56 гц 440 гц

Очевидно, что высота звука определяется его частотой: чем больше частота колебаний в звуковой волне, тем выше звук.

И еще одна характеристика звука — это тембр.

Тембром называют особое качество звука, его окраску, характерную для каждого голоса или музыкального инструмента. От чего же зависит тембр звука? Если подключить микрофон и пропеть какую-нибудь мелодию, то на экране осциллографа появится не синусоида, а более сложная кривая(график снизу), это значит, что источник звука совершает несинусоидальные колебания.

Такое колебание может быть представлено в виде суммы гармонических колебаний с разными частотами. Колебания с наименьшей частотой называются основным тоном, а колебания с более высокой частотой называются обертоном или гармоникой. Тембр звука определяет его окраску. Он определяется наличием и интенсивностью обертонов — частот, кратных основной.

Как извлечь звук на гитаре? Вы скажете, надо оттянуть струну и отпустить её. Рассмотрим аналог струны — резиновый шнур, т.к. он колеблется с меньшей частотой, то мы может наблюдать эти колебания.

2 этап. Создание стоячей механической волны.

Соберём установку для получения стоячей механической волны:

конец резинового резинового шнура к электронному усилителю мощности а другой к штативу, как показано на фото слева. 2) Подключим усилитель мощность к LabQuest последовательно с компьютером. 3) Откроем на компьютере программу Logger Pro и зададим такую частоту, чтобы получилась механическая волна с одной пучностью.

Это частота, равная 5 Гц. Далее поставим частоту 10Гц и получим стоячую волну с двумя пучностями(фото снизу).

Шнур, оттянутый строго посередине, будет совершать колебания. Через каждые пол периода весь шнур оказывается по разные стороны от положения равновесия. На концах шнура образуются узлы, а посередине — пучность, на длине шнура укладывается ровно половина длины волны. Мы видим возникновение стоячей волны.

Стоячие волны образуются в случае наложения двух волн одинаковой амплитуды, фазы и частоты, когда при «встрече» таких волн одна движется в прямом, а другая – в обратном направлении.

Стоячая волна это результат интерференции — явление наложения волн, приводящего к образованию интерференционной картины.

Частота стоячей волны с единственной пучностью называется основной частотой. Стоячие волны с более высокими частотами называются гармониками. Первой гармоникой называют основную частоту, вторая гармоника(фото снизу) имеет частоту, равную удвоенной основной и т.д.

Мы наблюдали стоячую волну в шнуре, как наглядный пример образования стоячей волны в звуковых колебаниях, которые нельзя увидеть, но можно услышать. При ударе по струне в ней тоже возникает стоячая волна с пучностью посередине(1).

3 этап. О струнах

Если бы каждая струна колебалась только с одной частотой, то все гитары имели бы практически одинаковое звучание. Но «голоса» гитар различаются. И во многом благодаря струнам.

Дело в том, что струна, помимо основного колебания, частота которого задается гитаристом при зажатии струны, участвует и в других колебаниях, больших частот и меньших амплитуд. Это кратные частоты. Их набор и определяет тембр. Сложное колебание с разными частотами хорошо заметно на басовых струнах(фото снизу)

В зависимости от упругих свойств материала струны (упругих свойств) эти частоты могут иметь разные амплитуды, т.е. разную громкость звучания на фоне звука основной частоты. А эти свойства определяются материалом, из которого струна изготовлена, ее толщиной, длиной и силой натяжения. Чем толще струна, тем ниже звук (меньше частота). Чем сильнее натянута струна, тем звук выше. Эти параметры задаются уже при установке струн и настройке гитары. При игре гитарист регулирует, по сути, только один параметр – длину струны, пережимая ее в разных местах. Чем меньше рабочая длина струны, тем выше частота колебаний (выше звук). Таким образом, увеличение натяжения струны приводит к повышению частот колебаний.

Сравним графики звуковых колебаний, полученных в программе Logger Pro камертона (ноты ля), (рисунок слева) с графиком этой же ноты, но сыгранной на гитаре (рисунок справа). Нетрудно увидеть, что у камертона синусоидальный график, а у гитары график с такой же частотой, но с некоторыми неровностями — это и есть обертоны.

А если сыграть на гитаре ля на октаву выше или ниже (рисунки слева, справа), то изменится и частота и набор обертонов.

Таким образом, каждая нота, сыгранная на любом инструменте, представляет собой сложный звук, состоящий из основного тона и большого числа обертонов.

4 этап. Ноты, созвучия и аккорды.

Рассмотрим ноты, созвучия и аккорды.

Современный нотный строй таков, что одноименные ноты соседних октав различаются по частоте в 2 раза. Например, «ля» первой октавы соответствует частоте 440 Гц, второй – 880 Гц, третьей – 1320 Гц и т.д. Созвучия, соответствующие разным интервалам, воспринимаются слухом и сознанием по-разному: одни звучат более приятно, другие – менее. Так как каждое созвучие – это одновременное звучание двух основных частот или результат сложения колебаний.

Если мы посмотрим на соотношения частот в разных созвучиях, построенных, например, от ноты «до», то увидим, что они таковы:

до-до диез 277,2 : 261,7 = 1,059.

до-ре 293,7 : 261,7 = 1,122.

до-ре диез 311,1 : 261,7 = 1,188. 1,2 = 6 : 5

до-ми 329,6 : 261,7= 1,259. 1,25 = 5 : 4

до-фа 349,2 : 261,7= 1,310. 4 : 3

до-соль 392,0 : 261,7 = 1,498. 1,5 = 3 : 2

до-ля 440,0 : 261,7 = 1,681.

до-си 493,9 : 261,7 = 1,887.

до-до(октава) 523,4 : 261,7 = 2 : 1

Поэтому аккорды — это не случайно подобранные красивые созвучия, а сочетания нот, частоты которых дают отношения целых чисел.

5 этап. Акустический резонатор.

Резонатор предназначен для эффекта усиления вынужденных колебаний, возникающих при несовпадении частот возмущающей силы и собственной частоты. Если поставить звучащий камертон на стол(фото справа), то доска стола приходит в вынужденные колебания и звук усиливается, но это объясняется увеличением площади колеблющейся поверхности, а не совпадением частот.

Но если камертон поставить на специальный резонаторный ящик, длина которого равна четверти длины звуковой волны, создаваемой камертоном, то слышимость звука камертона улучшается из-за резонанса в воздушной среде. Но почему же резонатор камертона — это простой ящик незамысловатой формы, в то время как корпус гитары представляет собой нечто более сложной формы? Дело в том, что если резонатор камертона должен усиливать звук только одной частоты, то резонатор гитары должен усиливать звуки разных частот.

6 этап. Рассмотрим подробнее устройство гитары.

Резонаторный ящик гитары, образованный двумя деками и боковиной, имеет особую форму. Расстояние от розетки до стенок ящика в разных местах разное, что и позволяет воздуху резонировать в ящике на разных частотах.Набор этих частот определяет общий тембр инструмента.

Наличие резонатора необходимо потому, что сама по себе струна плохой источник звука, т.к. она имеет маленькую площадь поверхность, а, следовательно, не может вызвать большие возмущения воздуха. Материал, из которого изготовлен корпус гитары, её форма, и даже лак, которым она покрыта, оказывают большое влияние на звучание инструмента. Знаменитый Страдивари создал гитары с неповторимым звучанием.

1. Б.М.Яворский, А.А.Детлаф, «Курс физики», М.,Высшая школа,1999

2. А.Радзишевский, «Основы аналогового и цифрового звука», Вильямс, 2006

Источник

Примеры вынужденных колебаний гитара

10. Математика колебания струны: тайное становится явным

Музыка есть таинственная арифметика души; она вычисляет, сама того не сознавая.

Ноябрьским утром 1717 г. на ступенях парижской церкви святого Жана ле Рона был найден младенец. Его взяли на воспитание и в честь святого церкви окрестили Жаном ле Роном. Мальчик рано проявил блестящий ум и жадную любознательность и вскоре стал гордостью всей Франции. Это был Жан ле Рон Д’Аламбер (1717-1783) — выдающийся французский математик, философ, писатель, член Парижской, Петербургской и других академий.

Круг интересов Д’Аламбера был необычайно широк: механика (принцип Д’Аламбера), гидродинамика (парадокс Д’Аламбера), математика (признак сходи мости Д’Аламбера), математическая физика (формула Д’Аламбера), философия теория музыки. Такой широты требовала и oабота вместе с Дени Дидро над созданием наменитой «Энциклопедии наук, искусств и ремесел», да и сам дух эпохи посвещения, когда к знаниям тянулись все, в том числе и «просвещенные деспоты» Фридрих II и Екатерина II. Последуя неоднократно приглашала Д’Аламбера быть воспитателем ее сына — цесаревича Павла, назначая при этом баснословное вознаграждение, но всегда получала деликатный, но твердый отказ.

Волновое уравнение (10.1) есть не что иное, как следствие второго закона Ньютона. Левая часть (10.1) выражает вертикальное ускорение струны в точке х, а правая часть — отнесенную к массе струны силу, вызывающую это ускорение, которая тем больше, чем больше вогнутость струны .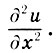

Д’Аламбер нашел общее решение уравнения (10.1)

которое содержит две произвольные функции φ(х,t) и ψ(х,t). Через пять лет Даниил Бернулли (1700-1782), математик, механик, физиолог и медик, почетный член Петербургской Академии наук, представитель славного рода Бернулли, который к настоящему времени подарил миру более 100 потомков, добившихся значительных результатов во всех сферах человеческой деятельности, и прежде всего в научной, получил другое общее решение уравнения (10.1)

Сравнивая решения Д’Аламбера (10.2) и Д. Бернулли (10.3), мы, казалось бы, приходим к абсурду: одно и то же уравнение (10.1) имеет совершенно непохожие решения! Но никакого абсурда здесь нет, так уж устроены дифференциальные уравнения. Они обладают бесчисленным множеством решений, что легко видеть из (10.2), где функции φ(x — at) и ψ(x + at) произвольные. При достаточно общих предположениях относительно функций φ и ψ правая часть (10.2) может быть представлена рядом (10.3).

Выбор того или иного частного решения дифференциального уравнения диктуется условиями, в которых протекает процесс (это так называемые граничные условия), и условиями, которые имели место в начале процесса (так называемые начальные условия). Только совокупность дифференциального уравнения, начальных и граничных условий определяет решение той или иной физической задачи. С помощью общего решения (10.2) Д’Аламбер решил одну из таких задач: найти колебания бесконечной струны (т. е. при отсутствии граничных условий), которой в начальный момент времени t = 0 придали некоторую форму f(х) и сообщили некоторое ускорение g(x). Математически задача ставилась так: найти решение уравнения (10.1), удовлетворяющее начальным условиям u(х,0) = f(x), u(х,0) = g(x), т. е. решить систему

Решение задачи (10.4) определяется формулой Д’Аламбера

Формула (10.5) в простейшем случае g(x) = 0, т. е. когда струну тихонько оттянули и отпустили, не придавая ей дополнительного ускорения, принимает вид

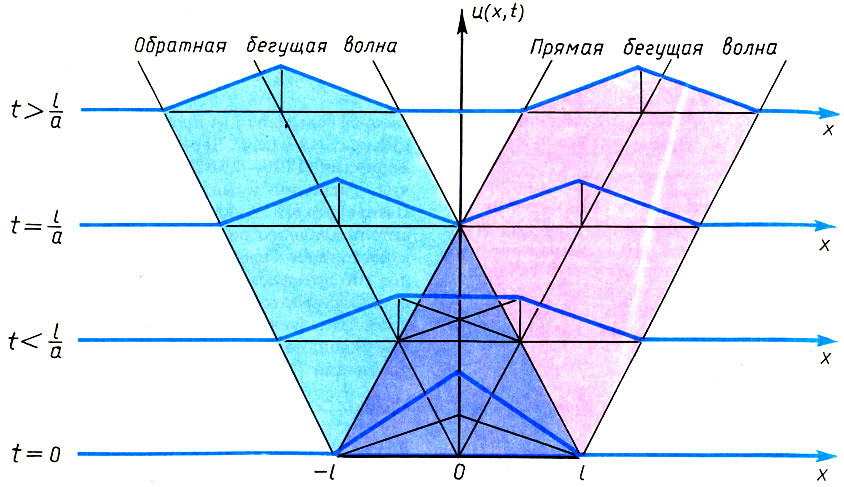
и физически означает, что сообщенный струне при t=0 профиль f(x) будет распространяться влево и вправо со скоростью а. Это так называемые две бегущие волны, движущиеся в противоположных направлениях с одинаковой скоростью а.

Начальное возмущение треугольной формы распадается на две бегущие волны. Профиль начального возмущения сохраняет свою форму, а его амплитуда уменьшается вдвое

На самом деле бесконечных струн не бывает. Струна имеет конечную длину l и, как правило, жестко закреплена на концах. Так возникают граничные условия: u(0,t) = 0 — струна закреплена слева (х = 0); и (l,t) = 0 — струна закреплена справа (х = l). Ясно, что в этом случае бегущие волны будут отражаться от концов, взаимодействовать друг с другом и образовывать более сложную картину колебаний.

Задача о колебании конечной струны была независимо решена Д’Аламбером и Эйлером, а еще через полвека Жозеф Фурье изобрел новый метод, позволявший решать эту и многие другие задачи математической физики. Задача о колебании конечной струны формулируется так: найти решение волнового уравнения (10.1), удовлетворяющее начальным условиям u(х,0) = f(х), u_t(x,0) = g(x) и граничным условиям u(0,t) = 0, u(l,t) = 0, т. е. решить систему

Жан Батист Жозеф Фурье (1768-1830) не был кабинетным ученым. Он взлетел на гребне Великой французской революции 1789 г. и из сына провинциального портного, готовившегося принять монашеский постриг, превратился в друга императора Наполеона. В 1798 г. Фурье участвовал в египетском походе Наполеона, где его жизнь не раз подвергалась опасностям. По возвращении из Египта Фурье занимался административной деятельностью, но находил время и для математических исследований. В 1807 г. он написал свою бессмертную работу «Математическая теория тепла». Главный математический результат Фурье можно описать так: при некоторых ограничениях всякую функцию f (х) можно представить в виде ряда (бесконечной суммы чисел или функций), называемого ныне рядом Фурье:

Фурье разработал метод решения уравнений типа (10.1), называемый методом разделения переменных Фурье.

Идея метода Фурье гениально проста. Решение уравнения (10.1) ищется в виде произведения двух функций X(х) и Т(t), каждая из которых зависит только от одной, «своей» переменной:

Замена (10.7) расщепляет уравнение (10.1) на два дифференциальных уравнения в обыкновенных «школьных» производных:

где λ — неизвестный вспомогательный параметр. Решая уравнения (10.8) и удовлетворяя начальным и граничным условиям (10.6) (разумеется, мы опускаем все промежуточные выкладки, которых здесь, как и при выводе формулы Д’Аламбера (10.5), хватит на несколько страниц), находят окончательное решение задачи (10.6) о колебании конечной струны:

Выясним физический смысл решения (10.9), и прежде всего функций u_n(х,t), составляющих это решение. Для этого выполним искусственное преобразование:

(Здесь мы воспользовались формулой синуса суммы двух аргументов и тем, что 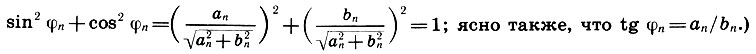Таким образом, u_n(х,t) можнс представить в виде

Из формулы (10.10) видно, что каждое решение u_n представляет собой гармоническое колебание (т. е. колебание по закону синуса) с одной и той же частотой 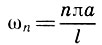и фазой φ_n. Амплитуда же колебаний А_n(х) для разных точек струны разная, т. е. зависит от координаты точки струны х. Из (10.10) видно, что при х = 0 и х = l А_n(0) = А_n(1) = 0, т. е. на концах струна неподвижна.

Итак, во времени колебания струны происходят с постоянной частотой ω_n, амплитуда колебания для каждой точки струны своя. При этом все точки струны одновременно достигают своего максимального отклонения в ту или другую сторону и одновременно проходят положения равновесия. Такие колебания называются стоячими волнами.

Пользуясь выражением для амплитуды стоячей волны (10.10) и учитывая, что 0≤x≤l, найдем неподвижные точки стоячих волн:

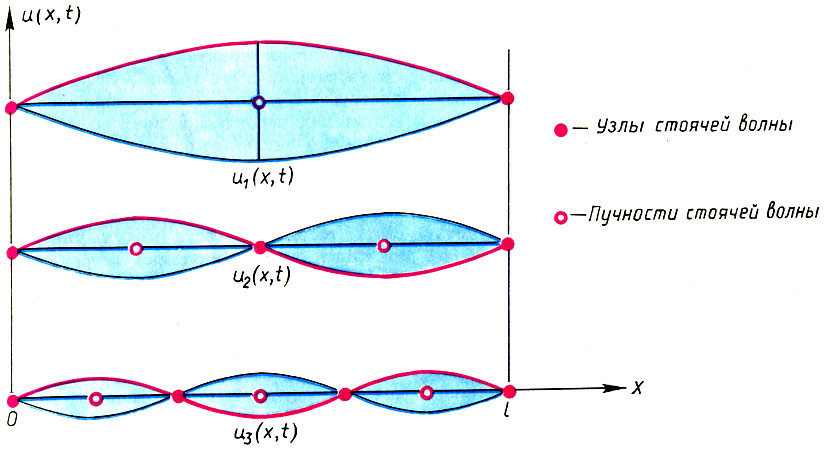
Неподвижные точки называются узлами стоячей волны. Ясно, что посередине между узлами расположены точки, в которых отклонения в стоячей волне достигают максимума. Эти точки называются пучностями стоячей волны.

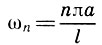
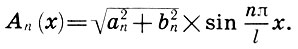
Сделаем общий вывод: колебание конечной струны представляет собой бесконечную сумму стоячих волн u_n(х,t), каждая из которых имеет постоянную частоту колебания и изменяющуюся по длине струны амплитуду В k-й стоячей волне имеется k

пучностей и (k + 1) узлов.

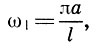
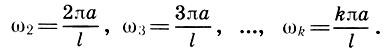
Перейдем теперь к «музыкальному содержанию» решения (10.9) и прежде всего к частотам колебаний. Мы пришли к выводу, что струна колеблется не только всей своей длиной, но одновременно и отдельными частями: половинками, третями, четвертями и т. д. Следовательно, струна издает звук не только основной частоты , но и призвуки частот . Тон основной частоты струны ω₁ называется основным тоном струны, а остальные тона, соответствующие частотам ω₂, ω₃, . ω_k, . называются обертонами (верхними тонами) или гармониками. Основной тон струны принимается за первый обертон (первую гармонику). Именно обертоны, сливаясь в общем звучании с основным тоном, придают звуку музыкальную окраску, называемую тембром.

Различие тембров музыкальных звуков в основном объясняется составом и интенсивностью обертонов у разных источников звуков. Чем больше у звука обертонов, тем красивее, «богаче» он нам кажется. По тембру, т. е. по составу обертонов, мы отличаем звуки одной и той же высоты и одинаковой громкости, воспроизведенные на скрипке или фортепиано, голосом или на флейте. Разумеется, и сам инструмент способен давать различные тембровые окраски, что прежде всего относится к скрипке.

Три первые стоячие волны (гармоники) колеблющейся струны. Колебания конечной струны U(х,t) представимы в виде суммы бесконечного числа стоячих волн usubn/sub(х,t)

У скрипачей есть особый способ необычного по тембру звукоизвлечения — игра флажолетами. Слегка дотрагиваясь пальцем до струны в узлах стоячих волн, но так, чтобы струна не соприкасалась с грифом, скрипач гасит одни обертоны и оставляет другие. В результате возникает мягкий, немного свистящий звук, напоминающий по тембру звучание старинного Деревянного духового инструмента — флажолета. Например, дотронувшись до струны точно посередине, скрипач гасит все гармоники, имеющие в этой точке пучности, и сохраняет только гармоники, имеющие в этой точке узлы, т. е. четные гармоники. Таким образом, самой низкой частотой станет второй обертон .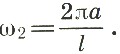

Но это не будет по тембру звук точно на на октаву выше основного тона 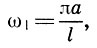, так как он будет составлен только из четных гармоник. Аналогично, дотронувшись до струны в точке l/3, скрипач оставит только гармоники, кратные трем: ω₃, ω₆, . и получит флажолет, не похожий на первый, даже если сделать ω₂ = ω₃. Игра флажолетами требует виртуозной точности. Ведь если мы не попадем точно в узел, то погасим вообще все гармоники и струна попросту не зазвучит!

Вот какую огромную роль играют в музыке слагаемые u_n(х,t) в решении (10.9). Их с полным правом называют звуковой краской музыканта. Но не только музыканты, а и создатели музыкальных инструментов проявляют постоянную заботу об этих слагаемых, от которых зависит тембр звука. Достаточно напомнить об особом «итальянском тембре» скрипок работ знаменитых итальянских мастеров XVI-XVIII веков, представителей нескольких поколений семей Амати, Гварнери, Страдивари.

Из решения (10.9), задавая нужным образом функции f(х) и g(x) и вычисляя интегралы, можно формально получить законы, которые экспериментально обнаружил английский ученый-энциклопедист Томас Юнг (1773 — 1829):

1. Если возбуждать струну в какой-либо точке, то в этой точке возникает пучность и не может образоваться узел.

2. Если затормозить струну в какой-либо точке, то в этой точке возникает узел и не может образоваться пучность.

Из первого закона Юнга следует, что если возбуждать струну, например, точно посередине, то в ней погасятся все гармоники, имеющие в этой точке узел, т. е. все четные обертоны. Значит, мы потеряем половину обертонов и звук станет блеклым. Ясно, что чем дальше от середины мы будем возбуждать струну, тем меньше первых, самых важных гармоник мы потеряем. Тембр звука от этого станет полнее и ярче. Вот почему смычок на скрипке, правая рука на гитаре, молоточки на фортепиано — все они возбуждают струну приблизительно на 1/7-1/10 доли струны от места ее закрепления. Делается это для того, чтобы не потревожить первые обертоны, а значит, не обеднить музыкальный звук. Что касается игры на скрипке флажолетами, то она основана на втором законе Юнга, который является обратным к первому закону.

Прежде чем расстаться с законами Юнга, скажем несколько слов об их создателе. Томас Юнг был удивительным человеком. » Всякий может делать то, что делают другие» — таков был девиз его жизни. И Юнг необычайно преуспел в исполнении этого нелегкого правила. Он был цирковым актером (акробатом и канатоходцем), авторитетным знатоком живописи, играл практически на всех су. Шествовавших в его время музыкальных инструментах, занимался расшифровкой египетских иероглифов, знал массу языков, в том числе латинский, греческий и арабский. И кроме всех этих «увлечений», Юнг получил блестящие результаты в науках: физике (волновая теория света), теории упругости (модуль упругости Юнга), оптике, акустике, астрономии, физиологии, медицине. Юнг написал около 60 глав научных приложений к знаменитой «Британской энциклопедии».

Рассмотрим подробнее основной тон струны. Вспоминая, что 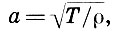, получим формулу для частоты основного тона:

откуда легко увидеть законы колебания струны, которые экспериментально обнаружили еще древние греки и которые затем переоткрыл и описал в своей «Универсальной гармонии» Марен Мерсенн:

1. Для струн одинаковой плотности и одинакового натяжения частота колебания обратно пропорциональна длине струны (это не что иное, как «первый закон Пифагора — Архита»; см. с. 101).

2. При заданной длине и плотности струны ее частота пропорциональна корню квадратному из натяжения.

3. При заданной длине и натяжении частота струны обратно пропорциональна корню квадратному из ее плотности. (При постоянной плотности чем толще струна, тем меньше частота ее колебаний, т. е. тем ниже звук.)

Разумеется, все эти законы (по крайней мере, качественно) можно было установить на монохорде.

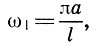
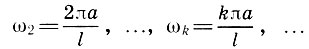
Но обратимся вновь к обертонам. Легко видеть, что частоты обертонов относятся как числа натурального ряда:

Таким образом, струна издает целый звукоряд тонов, называемый натуральным звукорядом. Теоретически натуральный звукоряд бесконечен. На практике же имеют значение первые 16 обертонов, так как остальные обертоны слишком мало отличаются друг от друга, обладают слишком малой энергией и фактически не слышны.

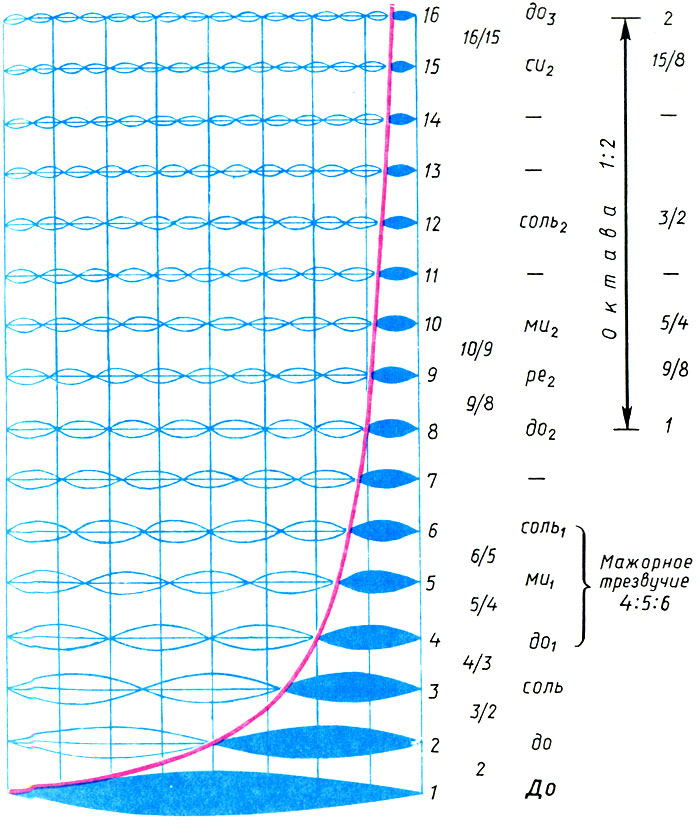
Натуральный звукоряд. Полагая ω₁ = l, частоты натурального звукоряда выражаются натуральным рядом чисел (ω_n = n). Натуральный звукоряд содержит все консонансы и все интервалы чистого строя

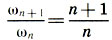
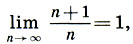
В самом деле, из (10.12) следует, что интервальный коэффициент двух соседних гармоник ω_n и ω_n+1 равен (n = 1, 2, 3, . ). Поскольку то мы легко приходим к выводу: с ростом номера п интервал между соседними гармониками натурального звукоряда уменьшается и в пределе стремится к чистой приме (унисону).

На рисунке показаны первые 16 гармоник колеблющейся струны, образующие натуральный звукоряд. Цифры справа обозначают частоты гармоник, считая ω₁ = 1, а красная линия (гипербола) отсекает часть струны 1/n, которая колеблется с частотой ω_n = n. Мы видим, что второй обертон и основной тон составляют интервал октавы ω₂/ω₁ = 2. Третий и второй обертоны — интервал квинты: ω₃/ω₂ = 3/2. Четвертый и третий — кварты: ω₄/ω₃ = 4/3. Пятый и четвертый — большой терции: ω₅/ω₄ = 5/4. Шестой и пятый — малой терции: ω₆/ω₅ = 6/5. Но ведь это есть не что иное, как набор совершенных и несовершенных консонансов! Таким образом, мы пришли к разгадке «закона консонансов» — «второго закона Пифагора — Архита» (с. 101 — 102): консонантные интервалы, которые математически выражаются отношением

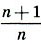
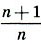
вида (n = 1, 2, 3, 4, 5), определены самой природой колебания струны! Все консонансы заключены в первых шести гармониках, т. е. первых шести тонах натурального звукоряда, причем по мере удаления от первой гармоники (основного тона) степень консонантности интервала убывает. Итак, закон целочисленных отношений для консонантных интервалов , который, по преданию, был экспериментально открыт Пифагором на монохорде, является следствием математического решения задачи о колебании струны и непосредственно вытекает из решения (10.9).

Переходя к более высоким гармоникам, нетрудно обнаружить также два интервала тона чистого строя: ω₉/ω₈ = 9/8, ω₁₀/ω₉ = 10/9 и интервал полутона чистого строя: ω₁₆/ω₁₅ = 16/15. Таким образом, все интервалы чистого строя содержатся в натуральном звукоряде! Вот почему чистый строй более приятен в гармоническом звучании, чем пифагоров строй.

Но и сами тона чистого строя (8.7) почти полностью определены натуральным звукорядом. В самом деле, если рассмотреть октаву между 8-й и 16-й гармониками, принимая частоту 8-й гармоники за единицу (т. е. поделив все частоты на 8), то мы обнаружим в этой октаве все ступени чистого строя, кроме 4-й (4/3) и 6-й (5/3). Следовательно, чистый строй почти целиком содержится в натуральном звукоряде.

Однако это коварное «почти» до сих пор составляет одну из загадок музыки. В самом деле, почему именно 7, 11 и 13-й обертоны (14-й обертон является октавным повторением 7-го) не входят ни в один из музыкальных строев? Знаменитый «фальшивый» 7-й обертон третье столетие не дает покоя теоретикам музыки! С одной стороны, ясно, что неправильно называть этот звук фальшивым, ибо он дан самой природой, которую трудно упрекнуть в фальши. Но с другой стороны, все теоретики музыки, начиная с Рамо, были слишком большими музыкантами, чтобы включить седьмую гармонику в какую-либо музыкальную систему (седьмой звук явно «резал ухо»!). Впрочем, еще в XVIII веке французский музыкальный теоретик Балльер с присущей французу легкостью писал: «Разница между древностью и современностью заключается в том, что тогда начинали считать диссонансы с 5-го призвука, а теперь начинают их считать лишь с 7-го». Не пойдет ли развитие музыки так, что в новых музыкальных системах найдется место и 7, и 11, и 13-му обертонам. А пока молоточки фортепиано, следуя первому закону Юнга, ударяют на 1/8 длины струны, чтобы максимально снизить силу злополучного 7-го обертона.

Наконец, отметим еще одну важную особенность натурального звукоряда. Глядя на рисунок, мы видим, что 4, 5 и 6-я гармоники образуют мажорное звучание (до-ми-соль). А если к ним добавить еще и 1-ю, и 2-ю гармоники, то получится мажорное трезвучие в сопровождении октавного баса! Итак, мажорное трезвучие составлено из ближайших гармоник (4, 5 и 6-й) основного тона (баса мажорного трезвучия). Следовательно, оно не только консонирует, но и обладает акустическим единством, заложенным в самой природе колебания струны. Это дало основание одному из последних универсальных ученых — немецкому математику, физику, физиологу и психологу Герману Гельмгольцу (1821 — 1894) утверждать, что «мажорный аккорд наиболее натурален из всех аккордов».

Ну а минорное трезвучие? Споры о природе минора не затихают и по сей день. В них участвовали Рамо, Д’Аламбер, Руссо, Гёте, Гельмгольц, многие наши современники. На сегодня мнения сходятся в том, что поскольку в минорном трезвучии (до — ми-бемоль — соль) второй звук (ми-бемоль) лежит на полутон ниже пятой гармоники основного тона, то он образует с ней едва слышимый диссонанс, который и обусловливает некоторую «затененность», «нечто мрачное и неясное, необъяснимое для слушателя» (Гельмгольц). По o этой причине в музыке Баха, Генделя, Моцарта минорные произведения часто заканчиваются мажорным — наиболее натуральным, просветленным — аккордом.

Итак, в мажорной гамме третья ступень как бы тяготеет вверх, тогда как в минорной она тяготеет вниз. Движение же вверх воспринимается нами как восхождение к свету, просветление, радость. Напротив, движение вниз ассоциируется со спуском в темноту, затемнением, печалью. Эти объективные предпосылки поддерживаются, кроме того, определенной традицией применения мажора и минора. В тех же случаях, когда эти традиции нарушаются, мы встречаем разудалую песню «Яблочко», написанную в миноре, и молитву «Ave Maria«, которую, несмотря на ее название — «Радуйся, Мария» — и мажорный лад, никак не назовешь веселой. К сожалению, смешивание объективных физико-математических законов строения мажора и минора с их субъективной эстетической оценкой породило вокруг них много ненужных споров.

В заключение остановимся еще на одной проблеме колеблющейся струны. До сих пор, следуя решению (10.9), мы пытались «разъять, как труп» колебания струны на простейшие гармонические составляющие. Но ведь на самом деле, опять же согласно (10.9), составляющие колебание струны гармоники складываются, образуя сложную картину колебаний. Характер этой картины зависит прежде всего от амплитуд гармоник. Решить эту задачу в общем виде не просто, поэтому остановимся на более простой задаче.

Пусть складываются два колебания постоянной и одинаковой амплитуды, равной для простоты единице, и разных частот ω₁

Источник