Расчет гитар токарных станков

Подбор сменных зубчатых колес. Программа для подбора

Программа для подбора сменных зубчатых колес

ПОРЯДОК ПОЛЬЗОВАНИЯ ТАБЛИЦАМИ / ПРОГРАММОЙ

Для подбора сменных колес искомое передаточное отношение выражается в виде десятичной дроби с числом знаков соответственно требуемой точности. В «Основных таблицах» для подбора зубчатых колес (стр. 16—400) находим колонку с заголовком, содержащим первые три цифры передаточного отношения; по остальным цифрам находим строку, на которой указаны числа зубьев ведущих и ведомых колес.

Требуется подобрать сменные колеса гитары для передаточного отношения 0,2475586. Сначала находим колонку с заголовком 0,247—0000, а под ним ближайшее значение к последующим десятичным знакам искомого передаточного отношения (5586). В таблице находим число 5595, соответствующее набору сменных колес (23*43) : (47*85). Окончательно получаем:

i = (23*43)/(47*85) = 0,2475595. (1)

Относительная погрешность сравнительно с заданным передаточным отношением :

δ = (0,2475595 — 0,2475586) : 0,247 = 0,0000037.

Строго подчеркиваем: во избежание влияния возможной опечатки нужно обязательно проверить полученное соотношение (1) на калькуляторе. В тех случаях, когда передаточное отношение больше единицы, необходимо выразить его обратную величину в виде десятичной дроби, по найденному значению в таблицах отыскать числа зубьев ведущих и ведомых сменных колес и поменять ведущие и ведомые колеса местами.

Требуется подобрать сменные колеса гитары для передаточного отношения i = 1,602225. Находим обратную величину 1:i = 0,6241327. В таблицах для ближайшего значения 0,6241218 находим набор сменных колес: (41*65) : (61*70). Учитывая, что решение найдено для обратной величины передаточного отношения, меняем местами ведущие и ведомые колеса:

i = (61*70)/(41*65) = 1,602251

Относительная погрешность подбора

δ = (1,602251 — 1,602225) : 1,602 = 0,000016.

Обычно требуется подбирать колеса для передаточных отношений, выраженных с точностью до шестого, пятого, а в отдельных случаях и до четвертого десятичного знака. Тогда семизначные числа, приведенные в таблицах, можно округлять с точностью до соответствующего десятичного знака. Если имеющийся комплект колес отличается от нормального (см. стр. 15), то, например, при настройке цепей дифференциала или обкатки можно выбрать подходящую комбинацию из ряда соседних значений с погрешностью, удовлетворяющей условиям, изложенным на стр. 7—9. При этом некоторые числа зубьев можно заменять. Так, если число зубьев комплекта не свыше 80, то

(58*65)/(59*95) = (58*13)/(59*19) = (58*52)/(59*76)

«пятковую» комбинацию предварительно преобразуют так:

а затем, по полученным множителям подбирают числа зубьев.

ОПРЕДЕЛЕНИЕ ДОПУСТИМОЙ ПОГРЕШНОСТИ НАСТРОЙКИ

Очень важно различать абсолютную и относительную погрешности настройки. Абсолютной погрешностью называют разность между полученным и требуемым передаточными отношениями. Например, требуется иметь передаточное число i = 0,62546, а получено i = 0,62542; абсолютная погрешность будет 0,00004. Относительной погрешностью называют отношение абсолютной погрешности к требуемому передаточному числу. В нашем случае относительная погрешность

δ = 0.00004/0,62546 = 0,000065

Следует подчеркнуть необходимость суждения о точности настройки по относительной погрешности.

Общее правило.

Если какая-либо величина А, получаемая настройкой через данную кинематическую цепь, пропорциональна передаточному отношению i, то при относительной погрешности настройки δ абсолютная погрешность будет Аδ.

Например, если относительная погрешность передаточного отношения δ =0,0001, то при нарезании винта с шагом t отклонение в шаге, зависящее от настройки, будет 0,0001 * t. Та же относительная погрешность при настройке дифференциала зубофрезерного станка даст дополнительное вращение заготовки не на требуемую дугу L, а на дугу с отклонением 0,0001 * L.

Если указан допуск на изделие, то абсолютное отклонение размера вследствие неточности настройки должно составлять только некоторую долю этого допуска. В случае более сложной зависимости какой-либо величины от передаточного отношения полезно прибегать к замене фактических отклонений их дифференциалами.

Настройка цепи дифференциала при обработке винтовых изделий.

Типичной является следующая формула:

где с — постоянная цепи;

β — угол наклона винтовой линии;

n — число заходов фрезы.

Продифференцировав обе части равенства, получим абсолютную погрешность di передаточного отношения

тогда допустимая относительная погрешность настройки

Если допустимое отклонение угла винтовой линии dβ выразить не в радианах, а в минутах, то получим

Например, если угол наклона винтовой линии изделия β = 18°, а допустимое отклонение в направлении зуба dβ = 4″ = 0′,067, то допустимая относительная погрешность настройки

δ = 0,067/3440*tg18 = 0,00006

Наоборот, зная относительную погрешность взятого передаточного отношения, можно по формуле (3) определить допущенную погрешность в угле винтовой линии в минутах. При установлении допустимой относительной погрешности можно в подобных случаях пользоваться тригонометрическими таблицами. Так, в формуле (2) передаточное отношение пропорционально sin β. По тригонометрическим таблицам для взятого числового примера видно, что sin 18° = 0,30902, а разность синусов на 1′ составляет 0,00028. Следовательно, относительная погрешность на 1′ составляет 0,00028 : 0,30902 = 0,0009. Допустимое отклонение винтовой линии — 0,067, поэтому допустимая погрешность передаточного отношения 0,0009*0,067 = 0,00006, такая же, как и при расчете по формуле (3). Когда оба сопряженных колеса нарезаются на одном станке и по одной настройке цепи дифференциала, то погрешности в направлении линий зубьев допускаются значительно большие, так как у обоих колес отклонения одинаковы и незначительно влияют только на боковой зазор при зацеплении сопряженных колес.

Настройка цепи обкатки при обработке конических колес.

В этом случае формулы настройки выглядят так:

i = p*sinφ/z*cosу или i = z/p*sinφ

где z — число зубьев заготовки;

р — постоянная цепи обкатки;

φ — угол начального конуса;

у — угол ножки зуба.

Пропорциональным передаточному отношению оказывается радиус основной окружности. Исходя из этого, можно установить допустимую относительную погрешность настройки

где α — угол зацепления;

Δα — допустимое отклонение угла зацепления в минутах.

Настройка при обработке винтовых изделий.

δ = Δt/t или δ = ΔL/1000

где Δt — отклонение в шаге винта за счет настройки;

ΔL — накопленная погрешность в мм на 1000 мм длины резьбы.

Величина Δt дает абсолютную ошибку шага, а величина ΔL характеризует по существу относительную погрешность.

Настройка с учетом деформации винтов после обработки.

При нарезании метчиков с учетом усадки стали после последующей термической обработки или с учетом деформации винта вследствие нагревания при механической обработке, процент усадки или расширения непосредственно указывает на необходимое относительное отклонение в передаточном отношении сравнительно с тем, какое получилось бы без учета этих факторов. В этом случае относительное отклонение передаточного отношения в плюс или минус является уже не ошибкой, а преднамеренным отклонением.

Настройка делительных цепей. Типичная формула настройки

где р — постоянная;

z — число зубьев или других делений на один оборот заготовки.

Нормальный комплект из 35 колес обеспечивает абсолютно точную настройку до 100 делений, так как в числах зубьев колес содержатся все простые множители до 100. В такой настройке погрешность вообще недопустима, так как она равна:

где Δl — отклонение линии зуба на ширине заготовки В в мм;

пD — длина начальной окружности или соответствующей другой окружности изделия в мм;

s — подача вдоль оси заготовки на один ее оборот в мм.

Только в грубых случаях эта погрешность может не играть роли.

Настройка зубофрезерных станков при отсутствии требуемых множителей в числах зубьев сменных колес.

В таких случаях (например, при z = 127) можно настроить гитару деления приближенно на дробное число зубьев, а необходимую поправку произвести, используя дифференциал [5]. Обычно формулы настройки гитар деления, подач и дифференциала выглядят так:

x = pa/z ; y = ks ; φ = c*sinβ/ma

Здесь р, k, с — соответственно постоянные коэффициенты этих цепей; а — число заходов фрезы (обычно а = 1).

Настраиваем указанные гитары согласно формулам

x = paA/Az+-1 ; y = ks ; φ’ = пc/asA

где z — число зубьев обрабатываемого колеса;

А — произвольное целое число, выбираемое так, чтобы числитель и знаменатель передаточного отношения разлагались на множители, подходящие для подбора сменных колес.

Знак (+) или (—) также выбирается произвольно, что облегчает разложение на множители. При работе правой фрезой, если выбран знак (+), промежуточные колеса на гитарах ставятся так, как это делают согласно руководству по работе на данном станке для правовинтовой заготовки; если выбран знак (—), промежуточные колеса ставят, как для левовинтовой заготовки; при работе левой фрезой — наоборот.

Желательно выбирать А в пределах

(1/2)*(пc/as) b+(20. 25); b + d > с+(20. 25) (11)

Эти условия ставятся для предотвращения упора сменных колес в соответствующие валы или детали крепления; числовое слагаемое зависит от конструкции данной гитары. Однако вторая из комбинаций (10) может быть принята только в том случае, когда колесо Z2 устанавливается на первом ведущем валу и если передача z2/z3 замедляющая или не содержит большого ускорения. Желательно, чтобы z2/z3 1) желательно так разбивать i = i1i2 чтобы сомножители были возможно более близкими один к другому и равномернее распределялось повышение скорости. При этом лучше, если i1 > i2

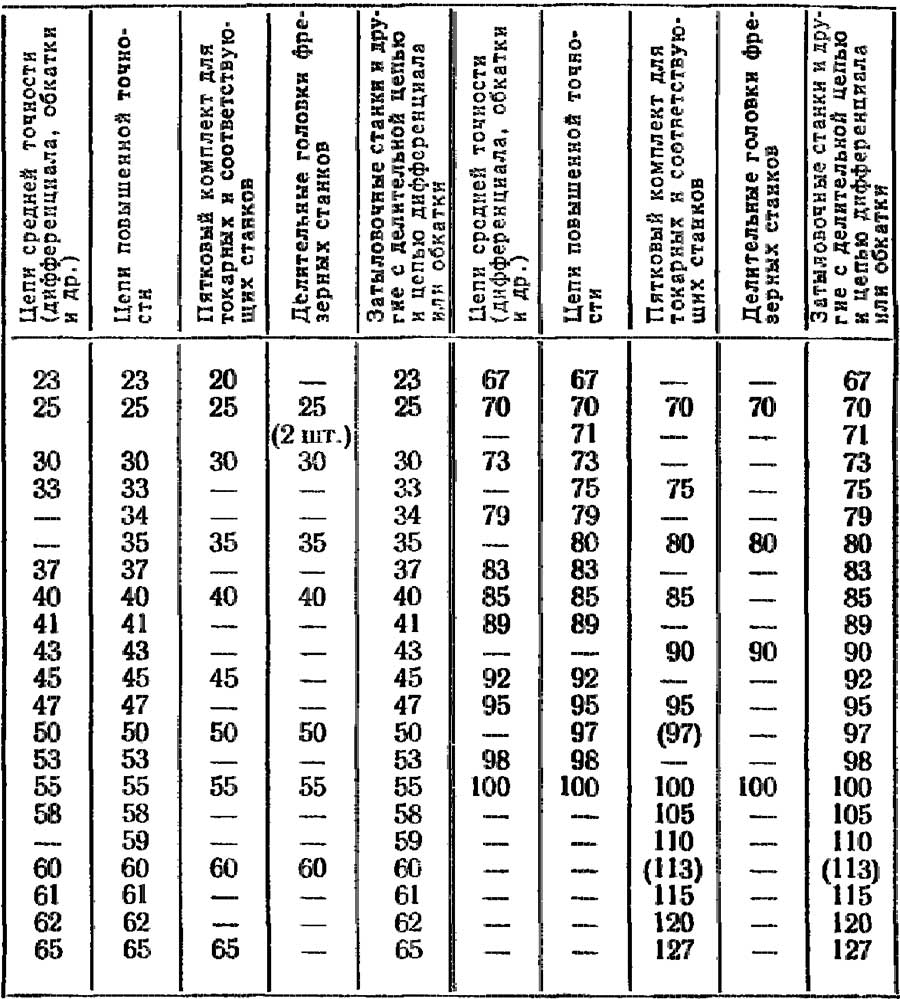
МИНИМАЛЬНЫЕ КОМПЛЕКТЫ СМЕННЫХ КОЛЕС

Состав комплектов сменных колес в зависимости от области применения приведен в табл. 2. В случае особо точных настроек — см. стр. 403.

Числа зубьев минимальных комплектов сменных колес для различных случаев настроек

Для настройки делительных головок можно использовать таблицы, прилагаемые заводом. Сложнее, но можно выбирать подходящие пятковые комбинации из приводимых в данной книге «Основных таблиц для подбора зубчатых колес».

Источник

Расчёт гитары деления. Как посчитать?

Расчёт гитары деления на зубофрезерный станок, пожалуй одно из самых необходимых действий при настройки станка. Считать гитару деления должен уметь каждый зуборезчик (на некоторых предприятиях в чертежах написана гитара деления).

Основная формула для расчётов — это отношение постоянной станка к количеству зубьев нарезаемой детали: c деления/количество зубьев. К примеру если постоянная станка 24, а нам необходимо нарезать 99 зубьев, то гитара деления будет выглядеть так — 24/99 (a/b). Ведущая шестерня 24, а ведомая 99. Иногда приходится разлаживать числа, так как шестерни могут не соединиться или постоянная такая что не поставишь, например есть постоянная 10, или число зубьев большое — от 127 и больше. Тогда гитара деления выглядит так — a/b c/d/. Шестерня a соединяется с шестерней b, которая на одном валу с шестерней c, шестерня c соединяется с шестерней d. Есть чуть другой вариант, главное что бы числитель не соединялся с числителем, а знаменатель со знаменателем и передаточное число соответствовало основному варианту — a/b. Всё это понятней на видео которое я сделал для вас:

Какие постоянные у зубофрезерных станков? Сильно долго не буду вникать в это, сразу по быстрому, постоянные которые знаю из личного опыта: 10, 15, 20, 24, 25, 30, 48, 60, 72. А вот к примеру постоянная на зубодолбёжном станке разная, это количество зубьев на долбяке.

В некоторых случаях гитара деления берётся из таблиц. К примеру на рейкофрезерный станок. На данном станке получается именно шаг определённого модуля. К примеру при обкатке или единичном делении на обычном зубофрезерном станке получается тоже шаг, но он получается путём деления окружности на равные части. В случаем же с рейкой — она может быть условно бесконечной, поэтому тут расчёт чуть другой именно на шаг. Таблица гитары деления на реечный станок, должна быть в паспорте данного станка.

Так же гитара деления считается по другим формулам, а проще взять сразу с таблица, на некоторые зарубежные станки. Например я сейчас начал работать на немецком зубофрезерном станке GFL там есть таблица.

Давайте я вам покажу на изображениях как считать гитару деления. К примеру посчитаем гитару деления с постоянной станка — 10, число зубьев — 60.

Давайте возьмём вариант чуть посложней, постоянная станка — 30, а нарезать надо 366 зубьев. Гитара деления будет с паразиткой (паразитка любая удобная шестерня которая служит для изменения вращения и не влияет на передаточное число). Итак:

В этом случае можно посчитать чуть по другому, но принцип не меняется.

Если есть вопросы, пишите в комментариях!

Поделится, добавить в закладки!

Источник

Практическая работа №5 «Настройка токарно-винторезного станка на нарезание заданной резьбы»

Опубликовано 29 Мар 2020 Рубрика: Механика |

Мастера, технологи и фрезеровщики механообрабатывающих цехов, в станочных парках которых есть зубофрезерные станки, регулярно сталкиваются при изготовлении косозубых цилиндрических зубчатых колес с вопросом максимально точного подбора шестеренок гитары дифференциала.

Если не вдаваться в подробности работы кинематической схемы зубофрезерного станка и технологического процесса нарезания зубьев червячной фрезой, то данная задача заключается в сборке двухступенчатого цилиндрического зубчатого редуктора с заданным передаточным отношением (u) из имеющегося комплекта сменных колес. Этот редуктор и есть гитара дифференциала. В комплект (приложение к станку) входит, как правило, 29 зубчатых колес (иногда более 50) с одинаковым модулем и диаметром посадочного отверстия, но с разным количеством зубьев. В наборе могут присутствовать по две-три шестерни с одинаковым количеством зубьев.

Схема гитары дифференциала изображена ниже на рисунке.

Настройка гитары дифференциала начинается с определения расчетного передаточного отношения (u) по формуле:

u=p*sin (β)/(m*k)

p – параметр конкретной модели станка (число с четырьмя-пятью знаками после запятой).

Значение параметра (p) индивидуально для каждой модели, приводится в паспорте на оборудование и зависит от кинематической схемы привода конкретного зубофрезерного станка.

β – угол наклона зубьев нарезаемого колеса.

m – нормальный модуль нарезаемого колеса.

k – число заходов червячной фрезы, выбранной для работы.

После этого необходимо выбрать из набора такие четыре шестерни с числами зубьев Z1, Z2, Z3 и Z4, чтобы, установленные в гитару дифференциала, они образовали редуктор с передаточным отношением (u’) максимально близким к рассчитанному значению (u).

(Z1/Z2)*(Z3/Z4)=u’≈u

Как это сделать?

Подбор чисел зубьев шестеренок, обеспечивающий максимальную точность, можно выполнить четырьмя способами (по крайней мере, известными мне).

Рассмотрим кратко все варианты на примере зубчатого колеса с модулем m=6 и углом наклона зубьев β=8°00’00’’. Параметр станка p=7,95775. Червячная фреза – однозаходная k=1.

Для исключения ошибок при многократных расчетах составим простую программу в Excel, состоящую из одной формулы, для расчета передаточного числа.

Ссылка на скачивание файла Excel: raschet-peredatochnogo-chisla-gitary-differentsiala (xls 34KB)

Расчетное передаточное число гитары (u) считываем

в ячейке D8: =D3*SIN (D6/180*ПИ())/D5/D4=0,184584124

Относительная погрешность подбора не должна превышать 0,01%!

δ=|(u-u’)/u|*100 Читайте также: Фрезерные станки с ЧПУ по мягким материалам

Вычисляем относительную погрешность выбранного варианта.

δ=|(u-u’)/u|*100=|(0,184584124-0,184584178)/0,184584124| *100=0,000029% Читайте также: Основные параметры вертикально-фрезерного станка 6Р13

Передаточное отношение трензеля 16К20 1 5 1 16К20 1,5 6 1 16К20 1,5 7,5 1 16К20 2 6 1 16К20 2 10 1 16К20 2,5 12,5 1 16К20 3 15 1 16К20 3,5 17,5 1 16К20 4 20 1 16К20 4,5 9 1

1. Расчет сменных зубчатых колес

а) Для расчета сменных зубчатых колес введем следующие обозначения:

Sp — шаг нарезаемой резьбы, мм;

Sx — шаг ходового винта, мм;

iтр = a/b — передаточное отношение трензеля;

i = (z1/z2)*(z3/z4) — передаточное отношение сменных зубчатых колес.

Из схемы (рисунок 1) следует, что за один оборот шпинделя ходовой винт сделает 1об шп* iтр* i оборотов и переместив суппорт и резец на расстояние 1об шп* iтр* i * Sx мм. Это перемещение резца за один оборот шпинделя равняется шагу резьбы Sp т.е. 1об шп* iтр* i * Sx = Sp мм.

Так как в большинстве случаев a=b, т.е. передаточное отношение трензеля iтр равно единице, то из уравнения получим i = Sp/Sx, т.е. передаточное отношение сменных зубчатых колес равно шагу нарезаемой резьбы деленному на шаг ходового винта.

Рисунок 1 – Схема передачи движения от шпинделя к ходовому винту при нарезании резьбы на токарно-винторезном станке

б) определим передаточное отношение сменных зубчатых колес по исходным данным:

Допустим, что на токарном станке с шагом ходового винта 6 мм требуется нарезать резьбу с шагом 2 мм. Для этого случая передаточное отношение сменных колес i = 2/6.

Следовательно, если соединить шпиндель и ходовой винт любой парой колес, передаточное отношение которых равно 2/6, то на детали получится резьба с шагом 2 мм.

Чтобы по передаточному отношению подобрать числа зубьев сменных колес

, нужно числитель и знаменатель дроби умножить на одно и тоже число таким образом, чтобы произведение получилось целым числом и равнялось числу зубьев, имеющихся в наборе сменных зубчатых колес. Например, если передаточное отношение i = 2/6, то умножая числитель и знаменатель соответственно на 10, 15 или 20, получим: i = 2*10/6*10 = 20/60, i = 2*15/6*15 = 30/90, i = 2*20/6*20 = 40/120.

Числа 20 и 60, 30 и 90, 40 и 120 обозначают соответственно числа зубьев отдельных пар сменных зубчатых колес, обеспечивающих получение на данном станке резьбы с шагом 2 мм. Нужно запомнить, что в числителе стоит число зубьев ведущего колеса, а в знаменателе — ведомого. Таким образом, колеса 20, 30 и 40 являются ведущими, а колеса 60, 90 и 120 — ведомыми.

Первое ведущее колесо из любой пары подобранных колес устанавливают на валу трензеля, а второе ведомое колесо из той же пары ставят на конец ходового винта.

Если требуемое передаточное отношение не может быть обеспечено одной парой колес, подбирают передачи с двумя, а иногда и тремя парами сменных колес. На рисунке 1 показана передача с двумя парами зубчатых колес.

в) из набора зубчатых колес выбираем 2 зубчатые пары так, чтобы выдержать передаточное отношение, определенное в пункте б).

передаточное отношение разложим на множители: 1*2/2*3 и каждый множитель умножаем на одно и то же число (например на 20), чтобы получить число зубьев из стандартного ряда.
Выбираем из «пяткового» набораz1= 20,z3= 40,z2= 40,z4= 60
i = (z1/z2)*(z3/z4) = 20/40 * 40/60 = 800/2400 = 2/6

2.2. Проверка правильности подсчета сменных зубчатых колес.

Чтобы проверить правильность подсчета сменных колес, нужно полученное передаточное отношение умножить на шаг ходового винта, при этом результат умножения должен дать шаг нарезаемой резьбы; это следует из формулы: Sp

Если же по формуле будет получен шаг резьбы, не соответствующий требуемому, то это покажет, что подсчет сменных колес сделан неверно.

а) Проверим правильность подсчета колес в предыдущем примере, где i = 20/40 * 40/60 и Sx =6 мм; Sp = i * Sx = 20/40 * 40/60 * 6 = 2 мм, т.е. колеса подобраны правильно.

2.3. Проверка сцепления сменных колес.

Подобранные расчетом колеса не всегда могут быть между собой сцеплены. Может случиться, что одно из них вплотную подойдет к пальцу гитары. Чтобы сменные зубчатые колеса можно было установить на гитаре, обеспечив их сцепление, необходимо выполнить следующее условие:

Сумма чисел зубьев первой пары колес (z1+z2) должна быть больше числа зубьев второго ведущего колеса (z3) не менее чем на 15, а сумма чисел зубьев второй пары колес (z3+z4) должны быть больше числа зубьев первого ведомого колеса (z2) тоже не менее чем на 15.

а) Проверим возможность сцепления колес, подобранных применительно к нашему примеру, где i = z1*z2/z3*z4 = 20/40 * 40/60.

— Разность между суммой чисел зубьев первой пары колес z1+z2 = 20+40 = 60 и числом зубьев z3 = 40 больше 15 и равно 20.

— Сумма чисел зубьев второй пары колес z3+z4 = 40+60 = 100 также больше числа зубьев z2 = 40 (разность равна 60). Следовательно, сцепление колес возможно.

Если бы условия сцепления не были выдержаны, то нужно сначала поменять местами ведомые или ведущие колеса. Если и такая перестановка не удовлетворит условиям сцепления, необходимо заново сделать подсчет.

1. Контрольные вопросы

1. В чем заключается настройка токарного станка для нарезания резьбы?
2. Как производится настройка станков?
3. Для чего служит первая группа шестерен?
4. Как определяется передаточное отношение нескольких пар зубчатых колёс?
5. Какие наборы шестерен применяются в качестве сменных колес?
6. Какие зубчатые колёса содержит «чётный» набор сменных зубчатых колёс?
7. Какие зубчатые колёса содержит «пятковый» набор сменных зубчатых колёс?
8. Какие два способа подбора сменных зубчатых колес обычно применяют на практике?

Вывод: в ходе выполнения практической работы ….

Настройка гитары по таблицам справочника.

С помощью таблиц справочника М.И. Петрика и В.А. Шишкова «Таблицы для подбора зубчатых колес» можно быстро решить рассматриваемую задачу. Методология работы подробно и понятно описана в самом начале книги.

Стандартный комплект В.А. Шишкова содержит 29 зубчатых колес с числами зубьев: 23; 25; 30; 33; 37; 40; 41; 43; 45; 47; 50; 53; 55; 58; 60; 61; 62; 65; 67; 70; 73; 79; 83; 85; 89; 92; 95; 98; 100.

Используем этот набор в решении нашей задачи.

Результат подбора по таблицам:

Z1=23 Z2=98 Z3=70 Z4=89

u’=(23*70)/(98*89)=0,184590690

δ=|(u-u’)/u|*100=|(0,184584124-0,184590690)/0,184584124| *100=0,003557%

Конструкция коробки подач токарно-винторезного станка 16К20

Коробка подач станка — унифицированный узел 16Б20П.070

и является типовой конструкцией закрытой коробки с передвижными блоками.

Связь шпинделя и суппорта станка для обеспечения оптимального режима резания осуществляется с помощью механизма подач, состоящего из реверсирующего устройства (трензеля) и гитары, которые осуществляют изменение направления и скорости перемещения суппорта.

Коробка подач закреплена на станине ниже шпиндельной (передней) бабки и имеет несколько валов, на которых установлены подвижные блоки зубчатых колес и переключаемые зубчатые муфты. В правом положении муфты получает вращение ходовой винт, а в левом ее положении (как показано на рисунке) через муфту обгона вращается ходовой вал.

Чертеж коробки подач токарного станка 16к20

Схема коробки подач токарного станка 16к20

Регулировка коробки подач станка 16К20

При ремонте станка особое внимание следует обратить на правильность монтажа механизма переключения зубчатых колес, смонтированного на плите 38, которая крепится к корпусу 3, коробки подач. Во избежание нарушения порядка сцепления зубчатых колес коробки подач при сборке нужно совместить риски, нанесенные на шестернях 51 и 52.

Гитара дифференциала в режиме on-line.

Заходите на сайт по адресу: sbestanko.ru/gitara.aspx и, если ваша модель станка присутствует в списке исходных данных, то задаете параметры нарезаемого колеса и червячной фрезы и ждете результат расчета. Иногда считает долго, иногда не находит решений.

Для нашего примера сервис не представил решений для точностей 5 и 6 разрядов после запятой. Зато для точности 4 знака после запятой выдал 136 вариантов. Мол — ковыряйтесь!

Лучший из представленных on-line сервисом результатов:

Z1=23 Z2=89 Z3=50 Z4=70

u’=(23*50)/(89*70)=0,184590690

δ=|(u-u’)/u|*100=|(0,184584124-0,184590690)/0,184584124| *100=0,003557%

Источник