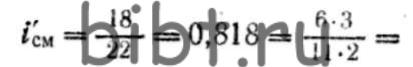§ 3. МЕТОДЫ ПОДБОРА СМЕННЫХ КОЛЕС ГИТАР.
(рис. 2) называется устройство, обеспечивающее правильное сцепление сменных зубчатых колес.
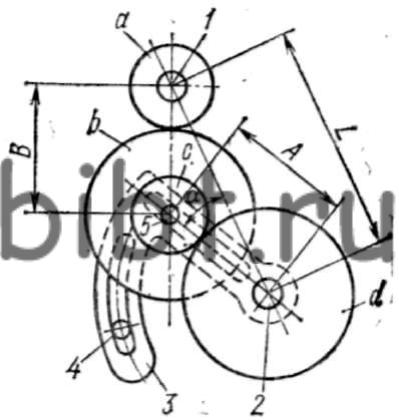
Рис. 2. Схема двухпарной гитары
Расстояние L между ведущим 1 и ведомым 2 валами является неизменным. На ведомом валу свободно установлен приклон гитары 3, закрепленный болтом 4. Ось 5 промежуточных колес b,с можно перемещать по радиальному пазу, тем самым изменяя расстояние А между центрами колес с и d. Дуговой паз позволяет регулировать размер В. Чтобы подобранные сменные зубчатые колеса не упирались во втулки валов 1, 2, необходимо соблюдать условия их сцепляемости:
При подборе колес необходимо учитывать и допускаемые пределы передаточных отношений пар сменных колес 1/5 с+(15-:-20) или 60+70>40+15;
c+d>b+(15-:-20) или 40+80>70+15.
Способ замены часто встречающихся чисел приближенными дробями заключается в том, что часто встречающиеся при нарезании дюймовых резьб, червяков и в других случаях числа π и 25,4 (числовое значение дюйма) заменяют приближенными значениями, удобными для подбора сменных колес, например:
1» ≈ 25,4 мм =127/5 мм; π≈22/7≈(19*21)/127 и т.д.
Полученная при этом погрешность не должна превышать заданной по условию. Абсолютная погрешность наладки
относительная погрешность наладки
где i см — заданное передаточное отношение; i’ см — полученное передаточное отношение сменных колес.
Способ подбора сменных колес на логарифмической линейке наименее точен. Край движка логарифмической линейки устанавливают против числа, соответствующего передаточному отношению гитары сменных колес. Передвижением бегунка находят риски, совпадающие на движке и на линейке. По полученным новым целым числам, которые дают при делении те же значения частного, подбирают числа зубьев сменных зубчатых колес:

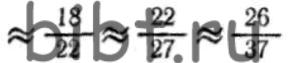
Выбирают наиболее точные и удобные значения i’ см для подбора колес: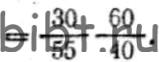
Способ подбора сменных колес по таблицам очень точен, но его следует применять лишь в тех случаях, когда нельзя подобрать колеса методом разложения на сомножители. Наиболее быстрый подбор сменных колес можно выполнить по таблицам, приведенным в работе [22].
Источник
Настройка гитары дифференциала

Если не вдаваться в подробности работы кинематической схемы зубофрезерного станка и технологического процесса нарезания зубьев червячной фрезой, то данная задача заключается в сборке двухступенчатого цилиндрического зубчатого редуктора с заданным передаточным отношением ( u ) из имеющегося комплекта сменных колес. Этот редуктор и есть гитара дифференциала. В комплект (приложение к станку) входит, как правило, 29 зубчатых колес (иногда более 50) с одинаковым модулем и диаметром посадочного отверстия, но с разным количеством зубьев. В наборе могут присутствовать по две-три шестерни с одинаковым количеством зубьев.
Схема гитары дифференциала изображена ниже на рисунке.
Настройка гитары дифференциала начинается с определения расчетного передаточного отношения ( u ) по формуле:
u = p *sin ( β )/( m * k )
p – параметр конкретной модели станка (число с четырьмя-пятью знаками после запятой).
Значение параметра ( p ) индивидуально для каждой модели, приводится в паспорте на оборудование и зависит от кинематической схемы привода конкретного зубофрезерного станка.
β – угол наклона зубьев нарезаемого колеса.
m – нормальный модуль нарезаемого колеса.
k – число заходов червячной фрезы, выбранной для работы.
После этого необходимо выбрать из набора такие четыре шестерни с числами зубьев Z1 , Z2 , Z3 и Z4 , чтобы, установленные в гитару дифференциала, они образовали редуктор с передаточным отношением ( u’ ) максимально близким к рассчитанному значению ( u ).
Как это сделать?
Подбор чисел зубьев шестеренок, обеспечивающий максимальную точность, можно выполнить четырьмя способами (по крайней мере, известными мне).
Рассмотрим кратко все варианты на примере зубчатого колеса с модулем m =6 и углом наклона зубьев β =8°00’00’’. Параметр станка p =7,95775. Червячная фреза – однозаходная k =1.
Для исключения ошибок при многократных расчетах составим простую программу в Excel, состоящую из одной формулы, для расчета передаточного числа.
Расчетное передаточное число гитары ( u ) считываем
в ячейке D8: =D3*SIN (D6/180*ПИ())/D5/D4 =0,184584124
Относительная погрешность подбора не должна превышать 0,01%!
δ =|( u — u’ )/ u |*100 u ) представляем приближениями в виде обычных дробей.
u =0,184584124≈5/27≈12/65≈79/428≈ 91/493 ≈6813/36910
Это можно сделать при помощи программы для представления многозначных констант приближениями в виде дробей с заданными точностями или в Excel подбором.
Выбираем подходящую по точности дробь и раскладываем ее числитель и знаменатель на произведения простых чисел. Простые числа в математике – это те, что делятся без остатка только на 1 и на себя.
u’ =91/493=0,184584178
91/493=(7*13)/(17*29)
Умножаем числитель и знаменатель выражения на 2 и на 5. Получаем результат.
Вычисляем относительную погрешность выбранного варианта.
δ =|( u — u’ )/ u |*100=|(0,184584124-0,184584178)/0,184584124| *100=0,000029% Z1 =23 Z2 =98 Z3 =70 Z4 =89
u’ =(23*70)/(98*89)=0,184590690
δ =|( u — u’ )/ u |*100=|(0,184584124-0,184590690)/0,184584124| *100=0,003557% Z1 =23 Z2 =89 Z3 =50 Z4 =70
u’ =(23*50)/(89*70)=0,184590690
δ =|( u — u’ )/ u |*100=|(0,184584124-0,184590690)/0,184584124| *100=0,003557% Уважающих труд автора приглашаю подписаться на анонсы статей, чтобы не пропустить появление возможно важной для вас информации (подписные формы — в конце статьи и наверху страницы).
Статьи с близкой тематикой
Отзывы
14 комментариев на «Настройка гитары дифференциала»
- tehotdel.nov 08 мая 2015 15:49
Пользуюсь вот Duncans Gear calculator, но хотелось бы оправославить все это дело в excel’е, т.к. там считаю передаточное — хотелось бы сразу все в одном месте иметь. Ума не приложу какие функции будут перебирать ряд колес (например, от 23 до 100) да еще чтоб дважды не перебирал одно и то же, считать их соотношение. А два числа сравнить то я уж сумею xD
Алгоритм решения этой задачи можно реализовать в Excel (Excel может всё!), но требуется поработать.
Ссылка на блок-схему алгоритма:
Ладно, скрипт так скрипт. Благодарю)
Александр, опираясь на Вашу статью разработал программу «Настройка гитары дифференциала» в VB6. Скачать ее можно на страничке twirpx.com/file/1676547/.
Использую ее в производстве.
Последнюю версию (значение угла можно вводить в формате ГГ.ММСС) могу выслать каждому желающему. (gerasimow1.narod.ru)
Спасибо за полезную информацию, как раз сейчас восстанавливаю себе зубофрезер 5к324. Для начала буду пользоваться Duncans, но на будущее планирую поставить электропривод, управляемый микроконтроллером, так, чтобы в сам микроконтроллер загонять данные колеса и фрезы, а он сам считал нужный коэффициент передачи и осуществлял с этим коэффициентом синхронизацию вращения шпинделя и стола.
Доброго времени . Подскажите где можно скачать программу настройки гитары дефферициала ? для мод 532 , К532А
Если Вы внимательно прочитаете еще раз статью, то сами ответите на свой вопрос.
Для модели 532 p=5,9683.
(p – параметр конкретной модели станка (число с четырьмя-пятью знаками после запятой)
У меня станок 5Е32П, а р я не знаю.Не подскажите?
Не подскажу. Поищите паспорт на свой станок в интернете.
Можете посчитать мне гитара дифференциала для шестерни
p – параметр конкретной модели станка (число с четырьмя-пятью знаками после запятой).
Значение параметра (p) индивидуально для каждой модели, приводится в паспорте на оборудование и зависит от кинематической схемы привода конкретного зубофрезерного станка.
β – угол наклона зубьев нарезаемого колеса.
m – нормальный модуль нарезаемого колеса.
k – число заходов червячной фрезы, выбранной для работы.
Какой набор колес для гитары дифференциала у вас есть в наличии (число зубьев / количество штук в наборе; полный список)?
Материал представляет интерес. Занимаемся вопросом давно. Можете выслать задание на создание набора колёс (минимальное и максимальное количества зубьев колёс набора, количество колёс в наборе, условие сцепляемости, другие требования) — решим. Можете выслать существующий набор — определим характеристики (диапазон реализуемых передаточных отношений и количество отношений, график плотности распределения в диапазоне, другое).
Здравствуйте, Александр! Проблема с настройкой станка 5324 на косозубую шестеню. Вернее, с самой кинематикой. Знаю, что для этого нужно разблокировать дифф-ал кулачковой муфтой. Та, что в паспотре на картинке не совсем понятна. Если я выложу кинематическую схему станка, Вы сможете подсказать, что и с чем нужно блокировать? Спасибо!
Андрей, здравствуйте. Ваш комментарий попал в спам, и я его не увидел. За 10 прошедших дней, думаю, разобрались с кинематикой?
Источник
Гитары сменных зубчатых колес. Подбор чисел зубьев сменных зубчатых колес Ремонт гитары сменных зубчатых колес токарный винторез
§ 3. МЕТОДЫ ПОДБОРА СМЕННЫХ КОЛЕС ГИТАР.
Гитарой (рис. 2) называется устройство, обеспечивающее правильное сцепление сменных зубчатых колес.
Рис. 2. Схема двухпарной гитары
Расстояние L между ведущим 1 и ведомым 2 валами является неизменным. На ведомом валу свободно установлен приклон гитары 3, закрепленный болтом 4. Ось 5 промежуточных колес b,с можно перемещать по радиальному пазу, тем самым изменяя расстояние А между центрами колес с и d. Дуговой паз позволяет регулировать размер В. Чтобы подобранные сменные зубчатые колеса не упирались во втулки валов 1, 2, необходимо соблюдать условия их сцепляемости:
При подборе колес необходимо учитывать и допускаемые пределы передаточных отношений пар сменных колес 1/5 с+(15-:-20) или 60+70>40+15;
c+d>b+(15-:-20) или 40+80>70+15.
Способ замены часто встречающихся чисел приближенными дробями заключается в том, что часто встречающиеся при нарезании дюймовых резьб, червяков и в других случаях числа π и 25,4 (числовое значение дюйма) заменяют приближенными значениями, удобными для подбора сменных колес, например:
1″» ≈ 25,4 мм =127/5 мм; π≈22/7≈(19*21)/127 и т.д.
Полученная при этом погрешность не должна превышать заданной по условию. Абсолютная погрешность наладки
относительная погрешность наладки
где i см — заданное передаточное отношение; i» см — полученное передаточное отношение сменных колес.
Способ подбора сменных колес на логарифмической линейке наименее точен. Край движка логарифмической линейки устанавливают против числа, соответствующего передаточному отношению гитары сменных колес. Передвижением бегунка находят риски, совпадающие на движке и на линейке. По полученным новым целым числам, которые дают при делении те же значения частного, подбирают числа зубьев сменных зубчатых колес.
У некоторых металлорежущих станков для наладки кинематических цепей применяют устройства, называемые гитарами (см. рисунок 11, г). Они обеспечивают необходимое сцепление сменных зубчатых колес. Для осуществления точных передаточных отношений используют двухпарные и трехпарные гитары. Каждая гитара снабжена определенным набором сменных колес.
Нормальные комплекты сменных зубчатых колес приведены, в таблице 4. Чтобы подобранные сменные зубчатые колеса могли поместиться на гитаре и не упирались во втулки валиков зубчатых колес, необходимо соблюдать следующие условия зацепляемости: а+Ь^Н-(15-22); с+ё^э+(15-22).
Суммы чисел сопряженных колес не должны превышать допустимого значения, определяемого конструкцией и размерами места, отведенного для размещения гитары на станке.
Существует несколько способов подбора чисел зубьев сменных зубчатых колес.
Способ разложения на простые множители применяют в том случае, если на них можно разложить числитель и знаменатель передаточного отношения, полученного по уравнению наладки.
Произведя разложение, сокращают дробь или вводят дополнительные множители, комбинируя их так, чтобы получить выражение дроби через числа зубьев, имеющихся в комплекте сменных колес.
 |
Способ замены часто встречающихся чисел приближенными дробями заключается в том, что часто встречающиеся числа 
приближенными величинами (таблица 7), дающими возможность с достаточной точностью получить передаточные отношения. Этот метод находит применение на токарно-винторезных станках при необходимости нарезания модульной или пит-чиевой резьбы, а также при нарезании дюймовой резьбы в случае отсутствия в наборе колеса с числом зубьев z=127.
П р и м е р 2. Подобрать сменные зубчатые колеса для нарезания дюймовой резьбы с числом ниток на один дюйм к=10 на токарно-винторезном станке с шагом винта рх, в = 6мм и постоянным передаточным отношением 1 П ост = 1-
Решаем этот пример пользуясь таблицей 7:
При применении приближенных способов подбора сменных колес, полученное передаточное отношение отличается от заданного, поэтому возникает необходимость в определении погрешности наладки. Например, в нашем случае
Абсолютная погрешность будет равна 0,42333-0,42307=0,00026
Например, для передаточного отношения
В соответствующей колонке таблиц В.А. Шишкова (см. таблицу 8) находим близкое значение логарифма lg i, которому соответствуют сменные зубчатые колеса гитары с передаточным отношением
В таблице 6 даны значения передаточных отношений меньше единицы, поэтому для i>l нужно брать логарифм обратной! величины передаточного отношения:
 |
Подбор чисел зубьев колес по логарифмической линейке. Край движка логарифмической линейки устанавливают против числа, соответствующего передаточному отношению. Передвижением визира находят риски, совпадающие на движке и на линейке. Риски должны соответствовать целым числам, которые дают при делении значение передаточного отношения. Затем подбирают числа зубьев сменных зубчатых колес, например, способом разложения на простые множители:
Оставив движок в полученном положении, передвигаем визир до тех пор, пока риски на движке и на линейке не совпадут. Тогда
Этот способ подбора колес при нарезании резьб применять, как правило нельзя, так как его точность обычно невысока.
Подбор чисел зубьев по таблицам М.В. Сандакова. Очень часто передаточное отношение содержит дробные числители и знаменатели или множители, некратные набору колес. В этом случае удобно подбирать числа зубьев зубчатых колес по таблицам М.В. Сандакова, содержащим 100 000 передаточных отношений. Заданное передаточное отношение в виде простой правильной дроби, неудобное для преобразования, нужно прежде всего обратить в десятичную дробь с шестью знаками после запятой. Если дробь неправильная, то необходимо разделить ее знаменатель на числитель, чтобы получить десятичную дробь меньше единицы. После этого в таблице находят десятичную дробь, равную полученной или ближайшую к ней, а рядом — соответствующую ей простую дробь. Получив простую дробь, далее
числа зубьев сменных колес подбирают обычным способом, например , от-
Гитара – это механизм со сменными зубчатыми колесами, предназначенный для ступенчатого изменения передаточного отношения расчетной кинематической цепи. Они применяются в основном в редко перенастраиваемых цепях при большом диапозоне и количестве передаточных отношений органа настройки расчетной цепи. Эти механизмы отличаются простотой конструкции. Основной недостаток гитар – трудоемкость настройки.
В станках используют гитары с одной, двумя и тремя парами сменных зубчатых колес. Гитара с одной парой сменных зубчатых колес (см. рис. 1.2) применяется в основном в цепях, не требующих точной настройки (органы настройки i v и i s ). Гитары с двумя и тремя парами сменных зубчатых колес используются, как правило, для точной настройки кинематических цепей (органы настройки i x , i y и т.п.). На рис. 2.19 показаны гитары с двумя и тремя парами сменных зубчатых колес.
Гитара с двумя парами колес (рис.2.19,а ) состоит из плиты 1, оси 2, фиксирующего болта 3 и сменных зубчатых колес a, в, c, d . Поскольку сумма зубьев сцепляемых колес при различных настройках различна, в плите гитары предусмотрен паз, позволяющий перемещать ось 2 и таким образом осуществлять зацепление сменных колес c и d различных диаметров. Болтом 3 фиксируют плиту гитары в требуемом положении для сцепления колес а и в.
Для подбора зубчатых колес пользуются единственным уравнением с четырьмя неизвестными
где i – передаточное отношение, полученное по ФН; a, b, c, d — числа зубьев колес гитары.
Число решений уравнения (*) ограничено следующими факторами:
Имеющимся набором сменных зубчатых колес;
а + в > с + (15…20) (**); с +d > в + (15…20) (***).
Для подбора сменных зубчатых колес используют в основном два следующих метода: основной и дополнительный.
Рис. 2.19. Гитары сменных зубчатых колес: а – с двумя парами
сменных колес; б – развертка гитары с двумя парами сменных
колес; в — гитара с тремя парами сменных колес
Основной метод – разложение на простые множители. Используется, когда i выражается простой дробью, числитель и знаменатель которой разлагаются на простые множители, удобные для подбора колес. Например,
Допустим, что в наборе сменных зубчатых колес станка имеются колеса с числами зубьев, кратными пяти от 20 до 100. Тогда,
Проверяем условия сцепляемости (**) по допустимому зачению
Возможно, что зубчатое колесо будет перерезать ведомый вал (рис.2.19,б) и, следовательно, монтаж колес невозможен. Поменяем местами колеса в числителе или знаменателе. Например,
Проверяем условия сцепляемости по большему допустимому значению: (**) 85 + 70 > 30 + 20; (***) 30 + 65 > 70 + 20.
Условия сцепляемости подтверждают возможность монтажа подобранных сменных зубчатых колес в гитаре.
Дополнительный метод – приближенный подбор. В этом случае используют способ непрерывных дробей или чаще табличный метод.
Пусть по формуле настройки i = 0, 309329. По таблицам (см., например, М.В. Сандаков и др. Таблицы для подбора шестерен: Справочник. – 6-е изд. М.: 1988. – 571 с.) подбираем соответствующую этой десятичной дроби простую дробь. После преобразований получим числа зубьев сменных колес

Такие зубчатые колеса имеются в нормальном наборе сменных зубчатых колес, например, зубофрезерных станков. Проверяем условия сцепляемости: (**) 21 + 65 > 45 + 20; (***) 45 + 47 > 65 + 20.
В ряде станков, например зубофрезерных, как правило, предусматривается более широкий диапозон настройки кинематических. Поэтому в таких станках используются гитары с тремя парами сменных зубчатых колес. В этих гитарах (рис.2. 19,в ) используется дополнительная пара зубчатых колес, а в ее плите выполняется два или три паза для промежуточных осей. Для подбора зубчатых колес используется уравнение с шестью неизвестными
Зубчатые колес e и f меняются значительно реже, чем колеса а,в,с,d . Как правило их передаточное отношение постоянно и равно 1; 1/2; 2. Это позволяет для данной пары колес использовать только четыре сменных зубчатых колеса, например с числами зубьев 40, 60, 60, 80.
Колеса а, в, с, d подбираются по правилам подбора колес для двухпарной гитары, а к условиям сцепляемости добавляется еще одно
Для различных групп станков комплекты сменных зубчатых колес различны. Однако все комплекты создаются на основе общего ряда чисел зубьев сменных колес: 20 – 23 — 25 – 30 – 33 – 34 – 37 – 40 — 41 – 43 – 45 – 47 – 50 – 53 – 55 – 58 – 59 – 60 – 62 – 65 – 67 – 70 – 71 – 73 -75 – 79 – 80 — 83 – 85 – 89 – 90 – 92 – 95 – 97 – 98 – 100 – 105 – 113 – 115 – 120 – 127 — всего 44 колеса.
Для токарно-винторезных станков принят набор колес, у которых числа зубьев кратны пяти (в комплекте 22 колеса).
Набор зубчатых колес для зуборезных станков ограничен колесом с числом зубьев 100. В затыловочных станках набор колес аналогичен общему, но в нем нет колеса со 113 зубьями. Для фрезерных станков (для настройки делительных головок) набор состоит из колес с числами зубьев: 25 – 25 – 30 – 35 – 40 – 50 – 55 – 60 – 70 – 80 – 90 – 100 (всего 12 колес).
Министерство общего и профессионального образования Российской Федерации
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Н.А. Молявко Н. Г. Переломов В.А. Шмаков
Кинематика и наладка. Учебное пособие
Часть 1
Работа 2. Настройка универсального зубофрезерного станка модели 5Д32 5
Работа 3. Настройка вертикального зубодолбежного станка модели 5В12 12
Работа 4. Настройка токарно-затыловочного станка модели 1Б811 16
Работа 5. Настройка зубофрезерного полуавтомата модели 5П23 20
Работа 6. Устройства кинематической настройки универсальных станков 24
Приложения 26
Санкт-Петербург
Современные металлорежущие станки — это высокоразвитые машины, включающие большое число механизмов и использующие механические, электрические, электронные, гидравлические, пневматические и другие методы осуществления движений и управления циклом. На станках обрабатывают как простые цилиндрические, так и поверхности, описываемые сложными математическими уравнениями.
Основы кинематики станков были разработаны проф. Г.М. Головиным. В разделе кинематики станков изучают методы кинематического расчета, наладки и формообразования деталей резанием.
При настройке кинематических цепей металлорежущих станков всегда движение одного конечного звена цепи строго координируется с движением другого конечного звена. В одних случаях требуется абсолютная точность в согласовании движений, в других — допускается некоторая погрешность, и согласование движений может быть приближенным.
Зубчатые колеса — одна из распространенных разновидностей деталей. Метод обкатки, обеспечивая высокую производительность и точность нарезания зубьев, дает возможность одним инструментом обрабатывать зубчатые колеса одного и того же модуля с любым числом зубьев.
Достаточно подробно рассмотрены кинематические структуры станков, реализующих метод обката, предназначенных для нарезания цилиндрических зубчатых колес с прямым и винтовым зубом, конических зубчатых колес с прямолинейным зубом. Некоторой спецификой обладают затыловочные станки, предназначенные для обработки задних поверхностей зубьев режущих инструментов. Особенностям настройки станков данного типа посвящен специальный раздел.
Материал пособия может служить дополнением к лекционному курсу. Его можно использовать при проведении лабораторных работ. В приложениях приведены индивидуальные задания для расчета настройки станков.
Работа 1. СПОСОБЫ ПОДБОРА СМЕННЫХ ЗУБЧАТЫХ КОЛЕС
Во многих станках звеном настройки в кинематических цепях является одно- или двух — парная гитара сменных зубчатых колес. После определения передаточного отношения звена настройки необходимо подобрать сменные зубчатые колеса гитары, тем самым, обеспечив конкретные расчетные перемещения конечных звеньев кинематической цепи. Точность настройки гитары зависит от назначения кинематической цепи. При этом могут быть использованы различные способы подбора сменных зубчатых колес: приближенный, способ Кнаппе, табличный и др. Обычно при настройке кинематических цепей станка приходится пользоваться вполне конкретным набором зубчатых колес, (такой набор сменных зубчатых колес поставляется со станком фирмой — изготовителем). Ограниченность набора приводит к тому, что не всегда возможно обеспечить абсолютное соответствие передаточного отношения эвена настройки заданному (расчетному) значению. Допускаемая погрешность настройки зависит от допускаемой погрешности заданного расчетного перемещения. Это можно показать на следующем примере.
Р
Рис. 1. Винторезная цепь токарного станка
ассмотрим кинематическую схему винторезной цепи токарного станка, представленную на рис.1,а. Назначение этой цепи: обеспечить нарезание на заготовке резьбы шага Т (варьируемый параметр) с помощью резца, связанного с ходовым винтом, имеющим постоянный шаг t.
Звено настройки — двух парная гитара сменных зубчатых колес с передаточным отношением i. Определим связь между погрешностью шага нарезаемой резьбы Т и погрешностью передаточного отношения i. Допустим, что с помощью набора сменных зубчатых колес обеспечивается передаточное отношение гитары i 1 , отличное от заданного i. Тогда абсолютная i и относительная погрешности определяются известными соотношениями: i = i — i 1 , =(i — i 1 )/ i .
При передаточном отношении гитары, равном i, шаг нарезаемой резьбы точно равен заданному: T = it .
Если передаточное отношение равно i 1 , то шаг нарезаемой резьбы будет отличен от заданного и равен: Ti = i 1 t.
Погрешность шага нарезаемой резьбы: Т = Т — Ti = t (I – i 1) = ti.
Следовательно, погрешность шага нарезаемой резьбы равна произведению шага ходового винта на абсолютную погрешность передаточного отношения звена настройки.
По такой схеме можно определять связь между погрешностью передаточного отношения звена настройки (гитары) и погрешностью расчетного перемещения и для других случаев.
Рассмотрим перечисленные выше способы подбора сменных зубчатых колес.
Способ замены заданного передаточного отношения приближенным
Этот способ применяется для настройки цепей, не требующих высокой точности (цепи главного движения, некоторые цепи подач). При его использовании заданное значение передаточного отношения заменяется простой дробью с небольшими значениями числителя и знаменателя, позволяющими затем перейти к конкретным числам зубьев сменных зубчатых колес.
Выбираем
Абсолютная погрешность: i=i-i 1 =0,044636.
Относительная погрешность:
Способ Кнаппе применяется для настройки кинематических цепей, у которых погрешность настройки должна быть минимальной (цепи обкатки, деления, дифференциала и др.). В основе способа лежит закономерность: если к числителю и знаменателю дроби прибавить (или вычесть) числа, находящиеся приблизительно в том же отношении, то значение дроби существенно не изменится. Последовательность подбора зубчатых колес по способу Кнаппе следующая:
а) записываем заданное передаточное отношение в виде простой дроби;
б) разбиваем полученную дробь на две — одну по величине примерно равную заданной с небольшими числителем и знаменателем и вторую — близкую к единице;
в) числитель и знаменатель второй дроби делим на разность между ними;
г) округляем полученные значения числителя и знаменателя;
д) преобразовываем эти дроби в конкретные числа зубьев сменных зубчатых колес.
Пример: Пусть задано передаточное отношение в виде десятичной дроби i= 0,944636
Абсолютная погрешность i=0,000364.
Относительная погрешность =0,039%.
Табличный способ
Применяется в тех случаях, когда необходима высокая точность настройки. Имеются специальные таблицы с переводом передаточных отношений, выраженных десятичными дробями, в простые дроби, числители и знаменатели которых можно разложить на сомножители, обычно не превышающие 47. По заданному передаточному отношению из таблицы выбирается ближайшее значение и соответствующая простая дробь, которая раскладывается на сомножители. Далее они преобразуются в числа зубьев сменных колес.
Пример. Задано передаточное отношение i = 0,944636.
Ниже приведена выдержка из таблицы
0,944606 324: 343
0,944633 836: 885
0,944643 529: 500
0,944653 1007: 1066
Ближайшее число в таблице
Ему соответствует решение:
Абсолютная погрешность передаточного отношения i=i-i 1 =0,000001. Данные таблицы применимы для комплекта сменных колес, в котором числа зубьев образуют арифметическую профессию с разностью, равной 5.
Условия зацепляемости сменных зубчатых колес
После определения чисел зубьев сменных зубчатых колес необходимо проверить их зацепляемость. Условия зацепляемости, которые определяют возможность установки колес в двухпарной гитаре (см. рис. 1,6), выражаются следующими неравенствами: R 1 +R 2 >R 3 ; R 3 +R 4 >R 2 , где Rj — радиусы делительных окружностей зубчатых колес.
Так как r i =mz i , то условия зацепляемости можно выразить через числа зубьев:
Эти соотношения не учитывают наружных размеров зубчатых колес и диаметров валов, на которых они устанавливаются. В окончательном варианте условия зацепляемости будут выглядеть следующим образом:
Пример. Проверим условие, зацепляемости колес, числа зубьев которых получены в предыдущем примере: Z 1 =84, Z 2 =68, Z 3 =65, z 4 =85. Имеем: 84+68=152 >80=65+15, 65+85=150>83=68+15, следовательно, условия зацепляемости выполняются.
1. Подобрать сменные колеса для двухпарной гитары станка тремя способами (передаточное отношение звена настройки задается преподавателем).
2. Определить абсолютную и относительную погрешности настройки каждым из способов.
3. Проверить условия зацепляемости подобранных сменных колес. При подборе использовать набор сменных зубчатых колес для гитар обкатки, подач и дифференциала станка 5Д32 (см. стр. 10).
1.Сандаковм.В. Таблицы для подбора шестерен. Москва-Свердловск. Маш-гиз,1960.
2. Петрик М.И. Прецизионные настройки гитар станков, м.: Машгиз, 1963.
3. Петрик М.И., Шишков В.А. Таблицы для подбора зубчатых колес. М.: Машгиз, 1964.
При вычислении передаточного отношения гитары производят деление на логарифмической линейке. Оставив движок неподвижным, передвигают визир и находят риски, совпадающие на движке и линейке.
На шкале линейки находим:
Используем второе отношение как наиболее точное:
Метод разложения на множители
Этот метод применим при небольших значениях числителя и знаменателя передаточного отношения.
Суть метода заключается в следующем:
Числитель и знаменатель разлагают на множители и, умножая на следующее число, находят числа зубьев сменных зубчатых колес.
Пример . Имеем: разлагаем дробь на множители.


(такие зубчатые колеса в комплекте станка имеются).
1. Авраамова Т.М., Бушуев В.В., Гиловой Л.Я. и др. Металлорежушие станки. Т.1. – М.: Машиностроение, 2011. – 608с.
2. Авраамова Т.М., Бушуев В.В., Гиловой Л.Я. и др. Металлорежушие станки. Т.2. – М.: Машиностроение, 2011. – 608с.
3. Ачеркан Н.С. Металлорежущие станки. – М.: Машиностроение, 1965, т. 1. – 764 С., т.2. – 628 с.
4. Ковалев Н.М., Переломов Н.Г. Фрезерные станки. – Л.: Машиностроение, 1964. – 110 с.
5. Кучер А.М., Кучер И.М., Ансеров Ю.М. Токарные станки и приспособления. – Л.: Машиностроение, 1969. – 376 с.
6. Кучер А.М., Киватицкий М.М., Покровский А.А. Металлорежущие станки, — Л.: Машиностроение 1972. – 305 с.
7. Металлорежущие станки: Учебник для машиностроительных втузов /Под редакцией В.Э. Пуша. – М.: Машиностроение, 1985. – 256 с.
8. Металлорежущие станки и автоматы: Учебник для машиностроительных втузов /Под ред. А.С. Проникова. – М.: Машиностроение, 1981. – 479 с.
10. Металлорежущие станки. Тепинкичиев В.К., Красниченко Л.В., Тихонов А.А., Колев Н.С. – М.: Машиностроение, 1970. – 464 с.
11. Металлорежущие станки: Учебное пособие для вузов по специальности “Технология машиностроения, металлорежущие станки и инструменты” /Н.С. Колев, Л.В. Красниченко, Н.С. Никулин и др. – М.: Машиностроение, 1980. – 500 с.
12. Назариков С.В. Настройка делительных головок. – Л.: Машиностроение, 1967. – 72 с.
13. Гулячкин К.Н. Лабораторные работы по курсу Металлорежущие станки. – М.: Машиностроение, 1963. – 230 с.
14. Руководство к лабораторным работам по курсу Металлорежущие станки /Под ред. П.Г. Петрухи. – М.: Высш. школа, 1973. – 150 с.
15. ГОСТ 12.4.113-82 ССБТ. Работы учебные лабораторные. Общие требования безопасности. – М.: Издательство стандартов, 1982. – 32с.
16. ГОСТ 12.4.026-76. Цвета сигнальные и знаки безопасности. – М.: Издательство стандартов, 1976. – 36 с.
17. ГОСТ 2.770-68. ЕСКД. Обозначения условные графические в схемах. – М.: ИПК Издательство стандартов, 2001. С 64 – 76.
18. ГОСТ 2.701-84. ЕСКД. Правила выполнения схем. – М.: Государственный комитет СССР по стандартам, 1987. – 136 с.
Источник