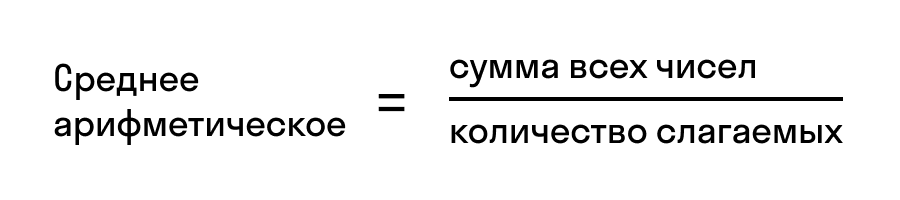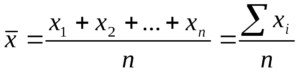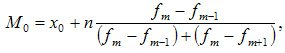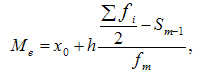Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
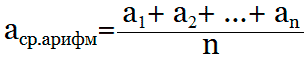
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
Источник
Среднее арифметическое пианино баян
Цели урока
Образовательные:
- ввести понятие среднего арифметического; вывести правило для его нахождения;
- научить решать задачи, связанные с нахождением среднего арифметического;
- отрабатывать навыки действий с десятичными дробями;
- развивать умение составлять задачи, используя цифровые данные из жизни.
Развивающие:
- содействовать развитию у школьников логического мышления, математической речи;
- способствовать развитию познавательного интереса;
- развивать умение анализировать, делать выводы на основе полученных результатов;
- способствовать формированию правильной математической речи;
- создать условия для развития у учащихся умений осуществлять самоконтроль и самооценку учебной деятельности.
Воспитательные:
- содействовать осознанию учащимися ценности изучаемого предмета;
- активизировать познавательную и творческую деятельность учащихся;
- показать значение математических знаний в жизни, побудить применять эти знания в жизни.
Тип урока: урок открытия новых знаний.
Формы работы: индивидуальная, фронтальная, групповая.
Оборудование: презентация к уроку, проектор, экран.
Предварительная подготовка.
Для эффективности работы было дано предварительное домашнее задание:
- класс поделен на 3 группы по рядам;
- измерить и записать рост каждого обучающегося в группе.
Ход урока:
I. Мотивирование к учебной деятельности (организационный момент) — 1-2 минуты
Посмотрите, всё ль в порядке:
Книжки, ручки и тетрадки.
Прозвенел сейчас звонок.
Учитель приветствует обучающихся, проверяет готовность к уроку, отмечает отсутствующих.
Каждый ученик получает лист «Моё настроение», на котором отмечает смайлик, соответствующий его настроению.
II.Актуализация и фиксирование индивидуального затруднения в пробном учебном действии — 4-5 минут
1.Устное решение задач.
Задача 1.
У Иванова Ивана по математике в журнале стоят оценки
4 5 3 4 5 4 3 3 4
Как вы думаете, какую оценку в четверти получит Иван? И почему?
Задача 2.
К доске приглашаются три ученика.
Вопросы:
Кто самый высокий?
Кто самый низкий?
Кто средний по росту?
Какие «особенные слова» вы заметили в условиях всех задач?
Часто мы и в жизни слышим фразы со словом “средний”, например: средний возраст, средний рост, средняя температура и т.д. Как вы понимаете эти выражения?
В математике тоже есть свои понятия со словом “средний” и сегодня мы познакомимся с одним из этих понятий.
2. Устный счёт.
Тема сегодняшнего урока состоит из двух слов. Вы её сможете прочитать, если верно решите примеры и вставите буквы в таблицу ответов.
7,3 · 3 Е
64,24 : 8 А
12 – 2,6 И
68,2 : 2 О
45,4 + 0,6 С
12 · 0,1 Р
43,1 · 10 Д
81,1 : 0,1 Н
60 – 0,9 Ф
4,13 + 3,87 М
6,45 – 6,4 Т
0,1 · 0,1 К
7 · 0,01 Ч
III. Постановка учебной задачи — 4-5 минут
Ребята, назовите тему урока. («Среднее арифметическое»)
Запишем число и тему урока.
Рассмотрим задачу:
У Ани 14 конфет, у Кати 9 конфет, а у Оли 10 конфет. Сколько конфет достанется каждой девочке, если конфеты разделить между ними поровну?
Решение обсуждается с учащимися.
14 + 9 + 10 = 33 (конфеты)
33 : 3 = 11 (конфет)
Число 11 называют средним арифметическим чисел 14; 9 и 10.
Рассмотрим еще задачу :
Миша, Петя и Коля были в походе. Подойдя к лесу, они решили сделать привал. У Миши было 2 пирожка, у Пети 4 и у Коли 6. Все пирожки мальчики разделили поровну и съели. Сколько пирожков съел каждый?
Совместно с учащимися получается:
2 + 4 + 6 = 12 (пирожков)
12 : 3 = 4 (пирожка)
Число 4 называется средним арифметическим чисел 2; 4 и 6.
Ребята, что же называется средним арифметическим чисел? ( Ответы учащихся)
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на число слагаемых.
Как найти среднее арифметическое нескольких чисел? (Ответы ребят)
Среднее арифметическое = (Сумма чисел) : (количество слагаемых)
(Учащиеся записывают в тетрадях)
IV. Открытие нового знания (построение проекта выхода из затруднения) 7-8 минут
Из какой сказки вы прослушали отрывок?
1. Братья сеяли три поля по 200 га каждое. На первом поле собрали 7220ц пшеницы, на втором – 7560ц, а на третьем – 7090ц пшеницы. Определите урожайность на каждом поле и найдите среднюю урожайность.
Вопросы:
Как найти урожайность одного поля?
Как найти среднюю урожайность трёх полей?
7220 : 200 = 36,1(ц.) – урожайность на первом поле.
7560 : 200 = 37,8(ц.) – урожайность на втором поле.
7090 : 200 = 35,45(ц.) – урожайность на первом поле.
(36,1 + 37,8 + 35,45) : 3 = 36,45(ц.) – средняя урожайность трёх полей.
- Задание на сообразительность:
Подключите свои знания, смекалку, сообразительность, чувство юмора и попытайтесь отыскать «среднее арифметическое» не чисел, а предметов, которые нас окружают.
Итак, среднее арифметическое:
- Велосипеда и мотоцикла. (Мопед.)
- Трамвая и поезда. (Электричка.)
- Апельсина и лимона. (Грейпфрут.)
- Туфельки и сапога. (Ботинок.)
- Пианино и баяна. (Аккордеон.)
- Холодильника и вентилятора. (Кондиционер.)
- Портфеля и рюкзака. (Ранец.)
- Носка и чулка. (Гольф.)
V. Первичное закрепление — 4-5 минут
1 . Задача № 1502 (из учебника)
Участница соревнований по фигурному катанию на коньках получила оценки
5,3; 4,8; 5,4; 5,0; 5,3; 5,4; 5,3; 5,2; 5,1.
Найдите среднюю оценку этой участницы.
Как найти среднее арифметическое нескольких чисел?
Решение с коментированием:
(5,3 + 4,8 + 5,4 + 5,0 + 5,3 + 5,4 + 5,3 + 5,2 + 5,1) : 9 = 5,2
2. Задача № 1504 (из учебника)
Поезд шёл 4 ч со скоростью 70 км/ч и 3ч со скоростью 84 км/ч. Найдите среднюю скорость поезда на пройденном за это время пути.
Как найти среднюю скорость?
Решение у доски по действиям или выражением:
(70 · 4 + 84 · 3) : 7 = 76(км/ч)
Средняя скорость =(Весь пройденный путь): (всё время движения).
3 . Игра – задание «Полёт в космос»
А сейчас мы с вами отправимся в космос, посетим планету Меркурий. Но до полета надо размяться, привести себя в форму, космическую.
Физминутка
Быстро встали, улыбнулись
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали. Сели, встали.
И на месте побежали.
Известно, что на планете Меркурий средняя температура +15°. Можно предположить, что возможна жизнь человека на этой планете. Но на самом деле температура на Меркурии колеблется от 150º мороза до 350°жары.
VI. Самостоятельная работа с самопроверкой по образцу (эталону) — 4-5 минут.
Тест по теме: «Среднее арифметическое чисел»
Ответ на вопрос обведите кружком
1. Найдите среднее арифметическое чисел 1,5 и 2,3
2. Среднее арифметическое чисел 2, 4, 6, и 0 равно:
3. Незнайка по математике получил следующие оценки 5, 3, 1, 4, 4, 1. Найдите среднюю оценку Незнайки.
4. Вини — Пух съел 18 конфет, Пятачок — 9 конфет, Кролик — 3 конфеты. Сколько конфет в среднем съел каждый?
5. Найдите среднее арифметическое чисел: 20,22 и 18,26
Источник
3 простых формулы, чтобы посчитать среднее арифметическое
О чем эта статья:
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Вот так:
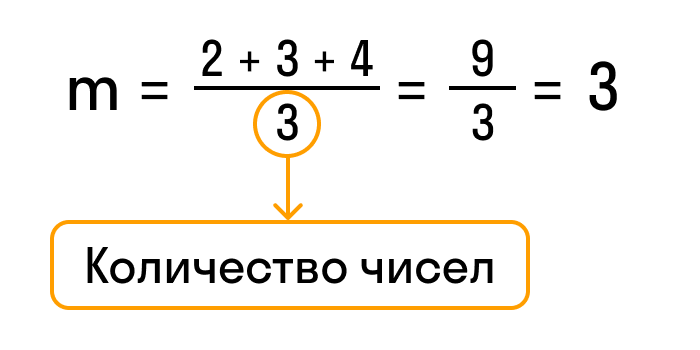
Например, найдем среднее арифметическое чисел 5, 6 и 7. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на три.
Так получилась формула среднего арифметического:
Способы вычисления среднего арифметического
Стандартная формула. Чтобы найти среднее арифметическое, нужно сложить все числа и поделить эту сумму на их количество. Формула выглядит так:
- x — среднее арифметическое;
- xⁿ — конкретное значение;
- n — количество значений.
- подходит при нормальном распределении значений в выборке;
- легко считать;
- интуитивно доступно.
- сложно представить распределение значений;
- можно запутаться в разных величинах.
Вычисление моды или наиболее часто встречающегося значения. Формула такая:
- M₀ — мода;
- x₀ — нижняя граница интервала, который содержит моду;
- n — величина интервала;
- fm — частота (сколько раз в ряду встречается то или иное значение);
- fm-1 — частота интервала предшествующего модальному;
- fm+1 — частота интервала следующего за модальным.
- подходит для формирования общественного мнения;
- подходит для нечисловых данных;
- доступно для понимания.
- моды может не быть при отсутствии повторов;
- мод может быть несколько (многомодальное распределение).
Не обязательно быть одаренным ребенком, чтобы хватать пятерки по математике. Нейробиологи говорят, что разница только в том, с какой скоростью дети учатся: обычный ребенок может выучить все то же самое, что и одаренный, только ему потребуется больше времени и усилий.
В современной школе Skysmart верят, что математика — для всех, просто каждому нужен свой подход. Запишите ребенка на бесплатный пробный урок, чтобы начать заниматься в своем темпе, с внимательным личным учителем и в удовольствие.
Вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. Если такого значения нет, за медиану принимают среднее число между границами половин выборки. Формула выглядит так:
- Mₑ — медиана;
- x₀ — нижняя граница интервала, который содержит медиану;
- h — величина интервала;
- f i — частота (сколько раз в ряду встречается то или иное значение);
- Sm-1 — сумма частот интервалов предшествующих медианному;
- fm — число значений в медианном интервале (его частота).
- дает самую реалистичную оценку;
- устойчива к выбросам.
- сложнее вычислить из-за необходимости упорядочивать.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: в магазине, на работе, в диалоге с другом или во время презентации перед инвесторами. Еще пригодятся, чтобы рассчитать среднюю скорость движения.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Посчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
В 5 классе можно искать среднее арифметическое с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Источник