- Расчет и конструкция октавной группы труб органа заданной октавы
- Обязательные элементы духовых музыкальных инструментов: голосовой механизм, мундштук, труба и раструб. Длина и диаметр октавной группы труб органа первой октавы. Масса соколеблющегося воздуха у входа закрытой трубы. Основной тон звучания закрытой трубы.
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
- Физические процессы в органных трубах
Расчет и конструкция октавной группы труб органа заданной октавы
Обязательные элементы духовых музыкальных инструментов: голосовой механизм, мундштук, труба и раструб. Длина и диаметр октавной группы труб органа первой октавы. Масса соколеблющегося воздуха у входа закрытой трубы. Основной тон звучания закрытой трубы.
| Рубрика | Музыка |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 15.12.2013 |
| Размер файла | 24,9 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Все духовые музыкальные инструменты состоят из таких обязательных элементов, как: голосовой механизм, мундштук, труба и раструб. Несмотря на важность каждого из элементов, все-таки основным звукообразующим элементом духового музыкального инструмента (ДМИ) является труба, а именно объем воздуха, заключенного в этой трубе. Труба принимает непосредственное участие в формировании звука, влияя на его громкость, тембр, высоту и т. д.
Колебания воздуха в трубе происходят в автоколебательном режиме на ее собственных частотах и из-за того, что эти колебания очень быстро затухают, необходима постоянная энергетическая подпитка для поддержания свободных колебаний. Автоколебания воздуха в трубе реализуется в виде стоячих волн. Свободные стоячие волны образуются только на собственных частотах трубы при поступлении внешней энергии неколебательного характера, например от постоянного потока воздуха.
В ДМИ используются трубы двух типов — открытые и закрытые. Под закрытыми трубами понимаются трубы с одним открытым и одним закрытым входами. Формирование стоячих волн подчиняется возможностям, которые определяются условиями на входах (концах) трубы. К примеру, на закрытом конце трубы воздух не может колебаться, следовательно, в этом месте должен образоваться узел, а на открытом конце трубы обязательно образуется «максимум» или пучность.
В данной работе рассматривается группа октавных труб закрытого типа, где необходимо рассчитать их параметры, а также выполнить эскиз.
Необходимо рассчитать длину и диаметр октавной группы труб органа первой октавы. Начиная с ноты «До» первой октавы и заканчивая нотой «До» второй октавы. Длину первой трубы рассчитаем, используя известное значение звука «До» первой октавы (261, 6 Гц) и соотношение, которое определяет частоту основного тона закрытой трубы:
Затем найдем ее диаметр, задавшись мензурой , из формулы:
Последующие длины труб будем рассчитывать из соотношения:
Диаметры этих труб найдем из . Длину и диаметр 13-ой трубы вычислим, зная значение ноты «До» второй октавы (523, 2 Гц). Результаты вычислений сведены в таблицу 1. 1
Источник
Физические процессы в органных трубах
Источник: « В мире науки » , №3, 1983. Авторы: Невиль Х. Флетчер и Сусанна Туэйтс
Величественное звучание органа создаётся благодаря взаимодействию строго синхронизированных по фазе воздушной струи, проходящей через разрез в трубе, и воздушного столба, резонирующего в её полости.
Ни один музыкальный инструмент не может сравниться с органом по силе, тембру, диапазону, тональности и величественности звучания. Подобно многим музыкальным инструментам, устройство органа постоянно совершенствовалось благодаря усилиям многих поколений искусных мастеров, медленно накапливавших опыт и знания. К концу XVII в. орган в основном приобрёл свою современную форму. Два наиболее выдающихся физика XIX в. Герман фон Гельмгольц и лорд Рэлей выдвинули противоположные теории, объясняющие основной механизм образования звуков в органных трубах, но из-за отсутствия необходимых приборов н инструментов их спор так и не был решён. С появлением осциллографов н других современных приборов стало возможным детальное изучение механизма действия органа. Оказалось, что как теория Гельмгольца, так и теория Рэлея справедливы для определённых величин давления, под которым воздух нагнетается в органную трубу. Далее в статье будут изложены результаты последних исследований, которые во многом не совпадают с объяснением механизма действия органа, приводимым в учебниках.
Трубки, вырезанные из камыша или других растений с полым стеблем, были, вероятно, первыми духовыми музыкальными инструментами. Они издают звуки, если дуть поперёк открытого конца трубки, или дуть в трубку, вибрируя губами, или, защемив конец трубки, вдувать воздух, заставляя вибрировать её стенки. Развитие этих трёх видов простейших духовых инструментов привело к созданию современной флейты, трубы и кларнета, из которых музыкант может извлекать звуки в довольно большом диапазоне частот.
Параллельно создавались и такие инструменты, в которых каждая трубка предназначалась для звучания на одной определённой ноте. Простейший из таких инструментов – это свирель (или «флейта Пана»), которая обычно имеет около 20 трубок различной длины, закрытых с одного конца и издающих звуки, если дуть поперёк другого, открытого конца. Самым большим и сложным инструментом этого типа является орган, содержащий до 10000 труб, которыми органист управляет при помощи сложной системы механических передач. Орган ведёт своё происхождение из глубокой древности. Глиняные фигурки, изображавшие музыкантов, играющих на инструменте из многих труб, снабжённых мехами, были изготовлены в Александрии ещё во II в. до н.э. К X в. орган начинает использоваться в христианских церквях, и в Европе появляются написанные монахами трактаты об устройстве органов. По преданию, большой орган, построенный в Xв. для Винчестерского собора в Англии, имел 400 металлических труб, 26 мехов и две клавиатуры с 40 клавишами, где каждая клавиша управляла десятью трубами. На протяжении последующих столетий устройство органа совершенствовалось в механическом и музыкальном отношении, и уже в 1429 г. в Амьенском соборе был построен орган, имевший 2500 труб. В Германии к концу XVII в. органы уже приобрели свою современную форму.
Орган, установленный в 1979 г. в концертном зале Сиднейского оперного театра в Австралии, является самым большим и технически совершенным органом в мире. Спроектирован и построен Р. Шарпом. В нем имеется около 10500 труб, управляемых с помощью механической передачи пятью ручными и одной ножной клавиатурами. Орган может управляться автоматически магнитной лентой, на которой в цифровой форме ранее было записано исполнение музыканта.
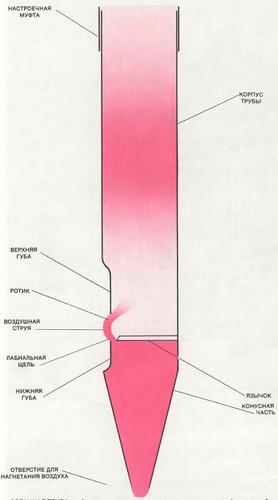
Термины, применяемые для описания устройства органа, отражают их происхождение от трубчатых духовых инструментов, в которые воздух вдувался ртом. Трубы органа сверху открыты, а снизу имеют суженную конусообразную форму. Поперёк сплющенной части, над конусом, проходит «ротик» трубы (разрез). Внутри трубы помешен «язычок» (горизонтальное ребро), так что между ним и нижней «губой» образуется «лабиальное отверстие» (узкая щель). Воздух нагнетается в трубу большими мехами и поступает в её конусообразное основание под давлением от 500 до 1000 паскалей (от 5 до 10 см вод. ст.). Когда при нажатии соответствующей педали и клавиши воздух входит в трубу, он устремляется вверх, образуя при выходе из лабиальной щели широкую плоскую струю. Струя воздуха проходит поперёк прорези «ротика» и, ударяясь о верхнюю губу, взаимодействует с воздушным столбом в самой трубе; в результате создаются устойчивые колебания, которые и заставляют трубу «говорить». Сам по себе вопрос, каким образом происходит в трубе этот внезапный переход от молчания к звучанию, очень сложен и интересен, но в данной статье он не рассматривается. Разговор в основном будет идти о процессах, которые обеспечивают непрерывное звучание органных труб и создают их характерную тональность.
Органная труба возбуждается воздухом, поступающим в её нижний конец и образующим струю при прохождении через щель между нижней губой и язычком. В разрезе струя взаимодействует с воздушным столбом в трубе у верхней губы и проходит то внутри трубы, то вне её. В воздушном столбе создаются установившиеся колебания, заставляющие трубу звучать. Давление воздуха, изменяющееся по закону стоячей волны, показано цветной штриховкой. На верхний конец трубы насаживается съемная муфта или заглушка, которые позволяют при настройке слегка изменять длину воздушного столба.
Может показаться, что задача описания воздушной струи, порождающей и сохраняющей звучание органа, полностью относится к теории потоков жидкостей и газов. Выяснилось, однако, что весьма трудно теоретически рассмотреть движение даже постоянного, плавного, ламинарного потока, что же касается полностью турбулентной струи воздуха, которая движется в органной трубе, то её анализ невероятно сложен. К счастью, турбулентность, представляющая собой сложный вид движения воздуха, в действительности упрощает характер воздушного потока. Если бы этот поток был ламинарным, то взаимодействие струи воздуха с окружающей средой зависело бы от их вязкости. В нашем случае турбулентность заменяет вязкость в качестве определяющего фактора взаимодействия в прямой зависимости от ширины воздушного потока. При строительстве органа особое внимание уделяется тому, чтобы воздушные потоки в трубах были полностью турбулентны, что достигается с помощью мелких нарезок по кромке язычка. Как ни удивительно, в отличие от ламинарного турбулентный поток устойчив и может быть воспроизведён.
Полностью турбулентный поток постепенно смешивается с окружающим воздухом. Процесс расширения и замедления при этом сравнительно несложен. Кривая, изображающая изменение скорости потока в зависимости от расстояния от центральной плоскости его сечения, имеет вид перевёрнутой параболы, вершина которой соответствует максимальному значению скорости. Ширина потока возрастает пропорционально расстоянию от лабиальной щели. Кинетическая энергия потока остаётся неизменной, поэтому уменьшение его скорости пропорционально корню квадратному из расстояния от щели. Эта зависимость подтверждается как расчётами, так и результатами эксперимента (при учёте небольшой области перехода вблизи лабиальной щели).
В уже возбуждённой и звучащей органной трубе воздушный поток попадает из лабиальной щели в интенсивное звуковое поле в прорези трубы. Движение воздуха, связанное с генерацией звуков, направлено через прорезь и, следовательно, перпендикулярно плоскости потока. Пятьдесят лет назад Б. Брауну из колледжа Лондонского университета удалось сфотографировать ламинарный поток задымлённого воздуха в звуковом поле. На снимках было отмечено образование извилистых волн, увеличивающихся по мере их продвижения вдоль потока, пока последний не распадался на два ряда вихревых колец, вращающихся в противоположных направлениях. Упрошенная интерпретация этих и подобных им наблюдений привела к неверному описанию физических процессов в органных трубах, которое можно найти во многих учебниках.
Более плодотворный метод изучения действительного поведения воздушной струи в звуковом поле заключается в экспериментировании с отдельно взятой трубой, в которой звуковое поле создаётся с помощью репродуктора. В результате таких исследований, проведённых Дж. Колтманом в лаборатории компании Westinghouse Electric Corporation и группой с моим участием в Университете Новой Англии в Австралии, были разработаны основы современной теории физических процессов, происходящих в органных трубах. Фактически ещё Рэлей дал тщательное и почти полное математическое описание ламинарных потоков невязких сред. Поскольку обнаружилось, что турбулентность не усложняет, а упрощает физическую картину воздушной струн, оказалось возможным использовать метод Рэлея с небольшими изменениями для описания воздушных потоков, экспериментально полученных и исследованных Колтманом и нашей группой.
Если бы в трубе не было лабиальной щели, то можно было бы ожидать, что воздушная струя в виде полосы движущегося воздуха просто смещалась бы назад и вперёд вместе со всем остальным воздухом в прорези трубы под воздействием акустических колебаний. В действительности же при выходе струи из щели она эффективно стабилизируется самой щелью. Этот эффект можно сравнить с результатом наложения на общее колебательное движение воздуха в звуковом поле строго сбалансированного смешения, локализованного в плоскости горизонтального ребра. Это локализованное смешение, которое имеет ту же частоту и амплитуду, что и звуковое поле, и в результате создаёт у горизонтального ребра нулевое смешение струи, сохраняется в движущемся потоке воздуха и создаёт извилистую волну.
Пять труб разной конструкции производят звуки одинаковой высоты, но разного тембра. Вторая труба слева – это дульсиана, обладающая нежным, тонким звучанием, напоминающим звучание струнного инструмента. Третья труба – открытый диапазон, дающий светлый, звонкий звук, который наиболее характерен для органа. У четвертой трубы звук сильно приглушённой флейты. Пятая труба – Waldflote ( « лесная флейта») с мягким звучанием. Деревянная труба слева закрыта заглушкой. Она имеет ту же основную частоту колебаний, что и другие трубы, но резонирует на нечётных обертонах, частоты которых в нечётное число раз больше основной частоты. Длина остальных труб не совсем одинакова, так как для получения одинаковой высоты тона производится «коррекция конца».
Как показал Рэлей для исследованного им типа струи и как мы всесторонне подтвердили для случая с расходящейся турбулентной струёй, волна распространяется вдоль потока со скоростью несколько меньшей половины скорости движения воздуха в центральной плоскости струи. При этом по мере движения вдоль потока амплитуда волны возрастает почти по экспоненте. Как правило, она увеличивается вдвое при перемещении волны на один миллиметр и её воздействие быстро становится преобладающим по отношению к простому возвратно-поступательному боковому перемещению, вызываемому звуковыми колебаниями.
Было установлено, что наибольшая скорость увеличения волны достигается в том случае, когда её длина вдоль потока в шесть раз превышает ширину потока в данной точке. С другой стороны, если длина волны оказывается меньше ширины потока, то амплитуда не увеличивается и волна может вообще исчезнуть. Поскольку воздушная струя расширяется и замедляет движение по мере удаления от щели, распространяться по длинным потокам с большой амплитудой могут только длинные волны, то есть низкочастотные колебания. Это обстоятельство окажется немаловажным при последующем рассмотрении создания гармонического звучания органных труб.
Рассмотрим теперь воздействие на воздушную струю звукового поля органной трубы. Нетрудно представить, что акустические волны звукового поля в прорези трубы заставляют кончик воздушной струи перемешаться поперёк верхней губы прорези, так что струя оказывается то внутри трубы, то вне её. Это напоминает картину, когда толкают уже раскачивающиеся качели. Воздушный столб в трубе уже колеблется, и, когда порывы воздуха входят в трубу синхронно с колебанием, они сохраняют силу колебаний, несмотря на различные потери энергии, связанные с распространением звука и трением воздуха о стенки трубы. Если же порывы воздуха не совпадают с колебаниями воздушного столба в трубе, они будут подавлять эти колебания и звук будет затухать.
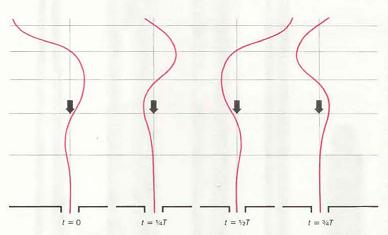
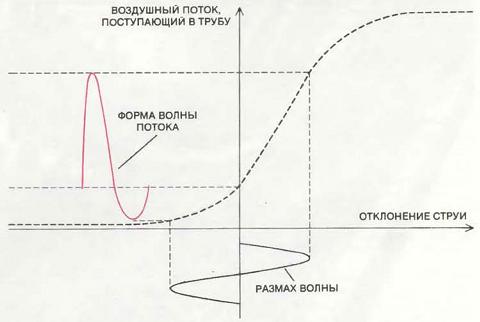
Форма воздушной струи показана на рисунке в виде ряда последовательных кадров при выходе из лабиальной щели в движущееся акустическое поле, создаваемое в «ротике» трубы воздушным столбом, который резонирует внутри трубы. Периодическое смещение воздуха в разрезе ротика создаёт извилистую волну, движущуюся со скоростью вдвое меньшей скорости движения воздуха в центральной плоскости струи и увеличивающейся по экспоненте, пока её амплитуда не превысит ширину самой струи. Горизонтальные сечения показывают отрезки пути, которые волна в струе проходит за последовательные четверти периода колебаний Т. Секущие линии сближаются с уменьшением скорости струи. В органной трубе верхняя губа расположена в месте, указанном стрелкой. Воздушная струя попеременно выходит из трубы и входит в неё.
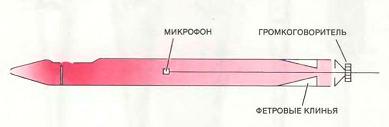
Измерение звукопроизводящих свойств воздушной струи можно осуществить, помещая в открытый конец трубы фетровые или пенопластовые клинья, препятствующие звучанию, и создавая звуковую волну небольшой амплитуды с помощью громкоговорителя. Отражаясь от противоположного конца трубы, звуковая волна взаимодействует у разреза «ротика» с воздушной струёй. Взаимодействие струи со стоячей волной внутри трубы измеряется с помощью переносного микрофона-тестера. Таким способом удается обнаружить, увеличивает или уменьшает воздушная струя энергию отраженной волны в нижней части трубы. Для того чтобы труба звучала, струя должна увеличивать энергию. Результаты измерения выражаются в величине акустической «проводимости», определяемой как отношение акустического потока на выходе из разреза « ротика» к звуковому давлению непосредственно за резрезом. Кривая значений проводимости при различных сочетаниях давления нагнетания воздуха и частоты колебаний имеет форму спирали, как показано на следующем рисунке.
Связь между возникновением акустических колебаний в прорези трубы и моментом поступления очередной порции воздушной струи на верхнюю губу прорези определяется отрезком времени, за который волна в воздушном потоке проходит расстояние от лабиальной щели до верхней губы. Мастера по изготовлению органов называют это расстояние «подрезом». Если «подрез» велик или давление (а следовательно, и скорость движения) воздуха низкое, то время движения будет большим. И наоборот, если «подрез» мал или давление воздуха высокое, то время движения будет небольшим.
Для того чтобы точно определить фазовое соотношение между колебаниями воздушного столба в трубе и поступлениями порций воздушной струи на внутреннюю кромку верхней губы, необходимо более подробно изучить характер воздействия этих пропорций на воздушный столб. Гельмгольц считал, что главным фактором здесь является объем воздушного потока, доставляемого струёй. Поэтому для того, чтобы порции струи сообщали как можно больше энергии колеблющемуся воздушному столбу, они должны поступать в тот момент, когда давление у внутренней части верхней губы достигает максимума.
Рэлей выдвигал другое положение. Он доказывал, что, поскольку прорезь находится сравнительно недалеко от открытого конца трубы, акустические волны у прорези, на которые воздействует воздушная струя, не могут создавать большое давление. Рэлей считал, что воздушный поток, поступая в трубу, фактически наталкивается на преграду и почти останавливается, что быстро создаёт в нём высокое давление, которое и оказывает воздействие на его движение в трубе. Поэтому, по мнению Рэлея, воздушная струя будет передавать максимальное количество энергии в том случае, если она будет поступать в трубу в момент, когда максимальным будет не давление, а сам поток акустических волн. Сдвиг между этими двумя максимумами составляет одну четверть периода колебаний воздушного столба в трубе. Если провести аналогию с качелями, то это различие выражается в толкании качелей, когда они находятся в верхней точке и обладают максимальной потенциальной энергией (по Гельмгольцу), и в момент, когда они находятся в самой нижней точке и обладают максимальной скоростью (по Рэлею).
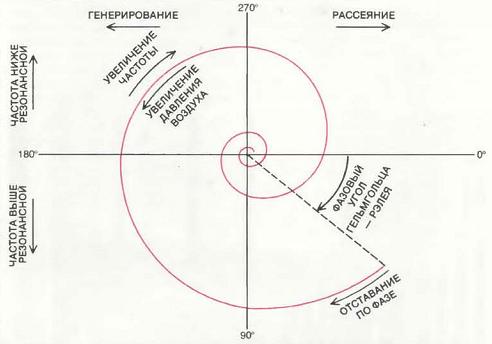
Кривая акустической проводимости струи имеет форму спирали. Расстояние от начальной точки указывает величину проводимости, а угловое положение – сдвиг фаз между акустическим потоком на выходе из прорези и звуковым давлением за прорезью. Когда поток совпадает по фазе с давлением, значения проводимости лежат в правой половине спирали и происходит рассеяние энергии струи. Для того чтобы струя генерировала звук, значения проводимости должны находиться в левой половине спирали, что имеет место при компенсации или задержке по фазе движения струи по отношению к давлению за разрезом трубы. В этом случае длина отраженной волны выше длины падающей волны. Величина опорного угла зависитот того, какой из двух механизмов доминирует в возбуждении трубы: механизм Гельмгольца или механизм Рэлея. При проводимости, соответствующей верхней половине спирали, струя понижает собственную резонансную частоту трубы, а когда значение проводимости находится в нижней части спирали, повышает собственную резонансную частоту трубы.
График движения воздушного потока в трубе (пунктирная кривая) при данном отклонении струи несимметричен по отношению к нулевой величине отклонения, поскольку губа трубы устроена так, чтобы разрезать струю не по её центральной плоскости. Когда отклонение струи происходит по простой синусоиде с большой амплитудой (сплошная кривая черного цвета), воздушный поток, поступающий в трубу (цветная кривая), «насыщается» сначала у одной крайней точки отклонения струи, когда она полностью выходит из трубы. При ещё большей амплитуде происходит насыщение воздушного потока и у другой крайней точки отклонения, когда струя полностью входит в трубу. Смещение губы придает потоку асимметричную волновую форму, обертоны которой имеют частоты, кратные частоте отклоняющей волны.
На протяжении 80 лет задача оставалась нерешённой. Более того, новые исследования фактически не проводились. И лишь теперь она нашла удовлетворительное решение благодаря работам Л. Кремера и X. Лизинга из Института им. Генриха Герца в Зап. Берлине, С. Эллера из Военно-морской академии США, Колтмана и нашей группы. Коротко говоря, и Гельмгольц, и Рэлей оба были отчасти правы. Соотношение между двумя механизмами воздействия определяется давлением нагнетаемого воздуха и частотой звука, причём механизм Гельмгольца оказывается основным при низких давлениях и высоких частотах, а механизм Рэлея – при высоких давлениях и низких частотах. Для органных труб стандартной конструкции механизм Гельмгольца играет обычно более важную роль.
Колтман разработал простой и эффективный способ изучения свойств воздушной струи, который был несколько модифицирован и усовершенствован в нашей лаборатории. В основе этого метода лежит изучение воздушной струи у прорези органной трубы, когда дальний конец её закрыт фетровыми или пенопластовыми звукопоглощающими клиньями, не дающими трубе звучать. Затем из репродуктора, помещённого у дальнего конца, вниз по трубе подаётся звуковая волна, которая отражается от края прорези сначала при наличии нагнетаемой струи, а потом без неё. В обоих случаях падающая и отражённая волны взаимодействуют внутри трубы, создавая стоячую волну. Измеряя с помощью небольшого микрофона-зонда изменения в конфигурации волны при подаче воздушной струи, можно определить, увеличивает или уменьшает струя энергию отражённой волны.
В наших экспериментах фактически измерялась «акустическая проводимость» воздушной струи, которая определяется отношением акустического потока на выходе из прорези, создаваемого присутствием струи, к акустическому давлению непосредственно внутри прорези. Акустическая проводимость характеризуется величиной и фазовым углом, которые можно представить графически в виде функции частоты или давления нагнетания. Если представить график проводимости при независимом изменении частоты и давления, то кривая будет иметь форму спирали (см. рисунок). Расстояние от начальной точки спирали указывает величину проводимости, а угловое положение точки на спирали соответствует запаздыванию фазы извилистой волны, возникающему в струе под воздействием акустических колебаний в трубе. Запаздывание на одну длину волны соответствует 360° по окружности спирали. Вследствие особых свойств турбулентной струи оказалось, что при умножении величины проводимости на квадратный корень из величины давления все величины, измеренные для данной органной трубы, укладываются на одной и той же спирали.
Если давление остаётся постоянным, а частота поступающих звуковых волн растёт, то точки, указывающие величину проводимости, приближаются по спирали к её середине по часовой стрелке. При постоянной частоте и увеличении давления эти точки удаляются от середины в противоположном направлении.
Внутренний вид органа Сиднейского оперного театра. Видны некоторые трубы его 26 регистров. Большая часть труб сделана из металла, некоторые изготовлены из дерева. Длина звучащей части трубы удваивается через каждые 12 труб, а диаметр трубы удваивается примерно через каждые 16 труб. Многолетний опыт мастеров – создателей органов позволил им найти наилучшие пропорции, обеспечивающие устойчивый тембр звучания.
Когда точка величины проводимости находится в правой половине спирали, струя отбирает энергию у потока в трубе, и поэтому происходит потеря энергии. При положении точки в левой половине струя передаст энергию потоку и тем самым действует как генератор звуковых колебаний. При положении значения проводимости в верхней половине спирали струя понижает собственную резонансную частоту трубы, а когда эта точка находится в нижней половине, струя повышает собственную резонансную частоту трубы. Величина угла, характеризующего отставание по фазе, зависит от того, по какой схеме – Гельмгольца или Рэлея – осуществляется основное возбуждение трубы, а это, как было показано, определяется величинами давления и частоты. Однако этот угол, отсчитываемый от правой части горизонтальной оси (правая четверть), никогда не бывает значительно больше нуля.
Поскольку 360° по окружности спирали соответствует отставанию по фазе, равному длине и извилистой волны, распространяющейся вдоль воздушной струи, величины такого отставания от значительно меньших четверти длины волны до почти трёх четвёртых её длины будут лежать на спирали от центральной линии, то есть в той части, где струя действует как генератор звуковых колебаний. Мы также видели, что при постоянной частоте отставание по фазе является функцией давления нагнетаемого воздуха, от которой зависят как скорость самой струи, так и скорость распространения извилистой волны вдоль струи. Поскольку скорость такой волны составляет половину скорости струи, которая в свою очередь прямо пропорциональна корню квадратному из величины давления, изменение фазы струи на половину длины волны возможно лишь при значительном изменении давления. Теоретически давление может меняться в девятикратном размере, прежде чем труба перестаёт производить звучание на своей основной частоте, если другие условия не нарушаются. На практике, однако, труба начинает звучать на более высокой частоте до достижения указанного высшего предела изменения давления.
Следует отметить, что для восполнения потерь энергии в трубе и обеспечения устойчивости звука, несколько витков спирали может уйти далеко влево. Заставить трубу звучать может только ещё один такой виток, местоположение которого соответствует примерно трём полуволнам в струе. Так как проводимость струн в этой точке низка, продуцируемый звук слабее любого звука, соответствующего точке на внешнем витке спирали.
Форма спирали проводимости может ещё больше усложниться, если величина отклонения у верхней губы превышает ширину самой струи. При этом струя почти полностью выдувается из трубы и вдувается в неё обратно на каждом цикле перемещения, и количество энергии, которую она сообщает отражённой волне в трубе, перестаёт зависеть от дальнейшего увеличения амплитуды. Соответственно снижается и эффективность воздушной струн в режиме генерации акустических колебаний. В этом случае увеличение амплитуды отклонения струи приводит лишь к уменьшению спирали проводимости.
Снижение эффективности струи мри увеличении амплитуды отклонения сопровождается возрастанием потерь энергии в органной трубе. Колебания в трубе быстро устанавливаются на более низком уровне, при котором энергия струи точно компенсирует потери энергии в трубе. Интересно отметить, что в большинстве случаев потери энергии вследствие турбулентности и вязкости значительно превышают потери, связанные с рассеянием звуковых волн через прорезь и открытый коней трубы.
Разрез органной трубы диапазонного типа, на котором видно, что язычок имеет насечку для соэданияоднородного турбулентного движения струи воздуха. Труба изготовлена из «краплёного металла» – сплава с большим содержанием олова и добавкой свинца. При изготовлении листового материала из этого сплава на нём закрепляется характерный рисунок, который хорошо виден на фотографии.
Разумеется, действительное звучание трубы в органе не ограничено одной определённой частотой, но содержит и звуки более высокой частоты. Можно доказать, что эти обертоны являются точными гармониками основной частоты и отличаются от неё в целое число раз. При постоянных условиях воздухонагнетания форма звуковой волны на осциллографе остаётся совершенно одинаковой. Малейшее отклонение частоты гармоник от величины, строго кратной основной частоте, приводит к постепенному, но чётко видимому изменению формы волны.
Это явление представляет интерес, потому что резонансные колебания воздушного столба в органной трубе, как и в любой открытой трубе, устанавливаются на частотах, которые несколько отличаются от частот гармоник. Дело в том, что при увеличении частоты рабочая длина трубы становится немного меньше из-за изменения акустического потока у открытых концов трубы. Как будет показано, обертоны в органной трубе создаются за счёт взаимодействия воздушной струи и губы прорези, а сама труба служит для обертонов более высокой частоты главным образом пассивным резонатором.
Резонансные колебания в трубе создаются при наибольшем движении воздуха у её отверстий. Другими словами, проводимость в органной трубе должна достигать своего максимума у прорези. Отсюда следует, что резонансные колебания и трубе с открытым длинным концом возникают на частотах, при которых в длине трубы укладывается целое число полуволн звуковых колебаний. Если обозначить основную частоту как f1, то более высокие резонансные частоты будут 2f1, 3f1 и т.д. (В действительности, как уже было указано, высшие резонансные частоты всегда немного превышают эти значения.)
В трубе с закрытым или заглушенным дальним конном резонансные колебания возникают на частотах, при которых в длине трубы укладывается нечётное число четвертей длины волны. Поэтому для звучания на той же самой ноте закрытая труба может быть вдвое короче открытой, и её резонансные частоты будут f1, 3f1, 5f1 и т.д.
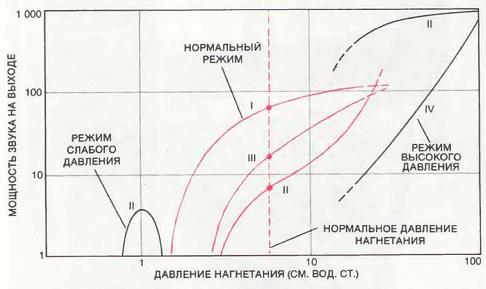
Результаты влияния изменения давления нагнетаеого воздуха на звук в обычной органной трубе. Римскими цифрами обозначены первые несколько обертонов. Главный режим трубы (в цвете) охватывает диапазон хорошо сбалансированного нормального звучания при нормальном давлении. При увеличении давления звучание трубы переходит на второй обертон; при понижении давления создается ослабленный второй обертон.
Теперь вернёмся к воздушной струе в органной трубе. Мы видим, что волновые возмущения высокой частоты постепенно затухают по мере увеличения ширины струи. Вследствие этого конец струи у верхней губы колеблется почти по синусоиде на основной частоте звучания трубы и почти независимо от более высоких гармоник колебаний акустического поля у прорези трубы. Однако синусоидальное движение струи не создаст такого же движения воздушного потока в трубе, поскольку поток «насыщается» за счёт того, что при крайнем отклонении в любую сторону он полностью течёт либо с внутренней, либо с внешней стороны верхней губы. Кроме того, губа обычно несколько смещена и разрезает поток не точно по его центральной плоскости, так что насыщение оказывается несимметричным. Поэтому колебание потока в трубе имеет полный набор гармоник основной частоты со строго определённым соотношением частот и фаз, а относительные амплитуды этих высокочастотных гармоник быстро возрастают с увеличением амплитуды отклонения воздушной струи.
В обычной органной трубе величина отклонения струи в прорези соизмерима с шириной струи у верхней губы. В результате в воздушном потоке создаётся большое число обертонов. Если бы губа разделяла струю строго симметрично, чётные обертоны в звучании отсутствовали бы. Поэтому обычно губе придаётся некоторое смешение, чтобы сохранить все обертоны.
Как и следовало ожидать, открытая и закрытая трубы создают звук разного качества. Частоты обертонов, создаваемых струёй, кратны основной частоте колебаний струи. Столб воздуха в трубе будет сильно резонировать на определённый обертон только при большой акустической проводимости трубы. При этом будет отмечаться резкое увеличение амплитуды на частоте, близкой к частоте обертона. Поэтому в закрытой трубе, где создаются лишь обертоны с нечётными номерами резонансной частоты, происходит подавление всех других обертонов. В результате получается характерный «глухой» звук, в котором чётные обертоны слабы, хотя и не отсутствуют полностью. Напротив, а открытой трубе получается более «светлый» звук, поскольку он сохраняет все обертоны, производные от основной частоты.
Резонансные свойства трубы в большой степени зависят от потерь энергии. Эти потери бывают двух типов: потери на внутреннее трение и теплоотдачу и потери на излучение через прорезь и открытый конец трубы. Потери первого типа более значительны в узких трубах и при низкой частоте колебаний. Для широких труб и при высокой частоте колебаний существенными являются потери второго типа.
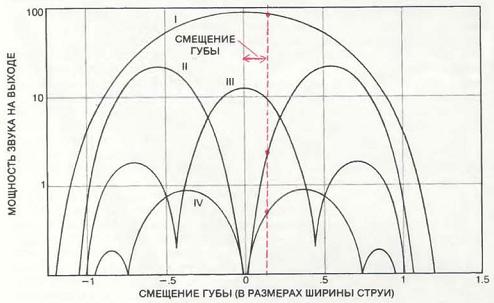
Влияние места расположения губы на создание обертонов свидетельствует о целесообразности смещения губы. Если бы губа разделяла струю строго по центральной плоскости, в трубе создавался бы только звук основной частоты (I) и третий обертон (III). При смещении губы, как показано пунктирной линией, возникают второй и четвёртый обертоны, значительно обогащающие качество звука.
Отсюда следует, что при данной длине трубы, а следовательно, и определённой основной частоте широкие трубы могут служить хорошими резонаторами только для основного тона и ближайших нескольких обертонов, образующих приглушенный «флейтоподобный» звук. Узкие трубы служат хорошими резонаторами для широкого диапазона обертонов, и поскольку излучение на высоких частотах происходит более интенсивно, чем на низких, то образуется высокий «струнный» звук. Между этими двумя звучаниями находится звонкий сочный звук, стать характерный для хорошего органа, который создаётся так называемыми принципалами или диапазонами.
Кроме того, в большом органе могут быть ряды труб с коническим корпусом, перфорированной заглушкой или иными разновидностями геометрической формы. Такие конструкции предназначены для модификации резонансных частот трубы, а иногда для увеличения диапазона высокочастотных обертонов с целью получения тембра особой звуковой окраски. Выбор материала, из которого изготавливается труба, не имеет большого значения.
Существует большое число возможных видов колебаний воздуха в трубе, и это в ещё большей степени усложняет акустические свойства трубы. Например, при увеличении давления воздуха в открытой трубе до такой степени, что в струе будет как раз создаваться первый обертон f1одной четверти длины основной волны, точка на спирали проводимости, соответствующая этому обертону, перейдёт на её правую половину и струя перестанет создавать обертон данной частоты. В то же время частота второго обертона 2f1 соответствует полуволне в струе, и он может быть устойчивым. Поэтому звучание трубы перейдёт на этот второй обертон, почти на целую октаву выше первого, причём точная частота колебаний будет зависеть от резонансной частоты трубы и давления нагнетания воздуха.
Дальнейшее увеличение давления нагнетания может привести к образованию следующего обертона 3f1 при условии, что «подрез» губы не слишком велик. С другой стороны, часто бывает, что низкое давление, недостаточное для образования основного тона, постепенно создаёт один из обертонов на втором витке спирали проводимости. Подобные звуки, создаваемые при излишке или недостатке давления, представляют интерес для лабораторных исследований, но в самих органах применяются крайне редко, лишь для достижения какого-то особого эффекта.
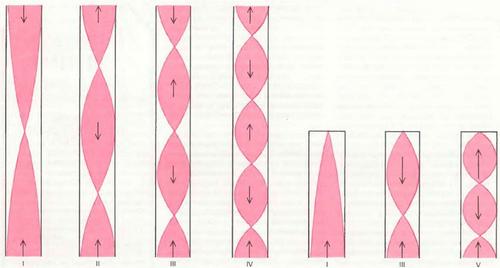
Вид стоячей волны при резонансе в трубах с открытым и закрытым верхним концом. Ширина каждой цветной линии соответствует амплитуде колебаний в различных частях трубы. Стрелками указано направление движения воздуха во время одной половины колебательного цикла; во второй половине цикла направление движения меняется на обратное. Римскими цифрами обозначены номера гармоник. Для открытой трубы резонансными являются все гармоники основной частоты. Закрытая труба должна быть вдвое короче для создании той же ноты, но для нее резонансными являются только нечетные гармоники. Сложная геометрия «ротика» трубы несколько искажает конфигурацию волн ближе к нижнему концу трубы, не меняя их « основного » характера.
После того как мастер при изготовлении органа сделал одну трубу, обладающую необходимым звучанием, основная и наиболее трудная его задача – создать весь ряд труб соответствующей громкости и гармоничности звучании по всему музыкальному диапазону клавиатуры. Этого нельзя достичь простым набором труб одинаковой геометрии, различающихся только своими размерами, поскольку у таких труб потери энергии от трения и излучения будут по-разному влиять на колебания различной частоты. Чтобы обеспечить постоянство акустических свойств по всему диапазону, необходимо варьировать целым рядом параметров. Диаметр трубы меняется при изменении её длины и зависит от неё как степень с показателем k, где k меньше 1. Поэтому длинные басовые трубы делают более узкими. Расчётная величина k составляет 5/6, или 0,83, но с учётом психофизических особенностей человеческого слуха она должна быть уменьшена до 0,75. Это значение kочень близко к тому, которое эмпирически определили великие мастера органов XVII и XVIII вв.
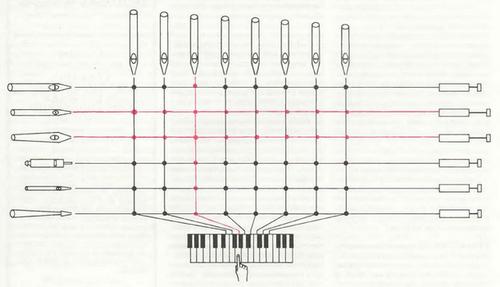
В заключение рассмотрим вопрос, важный с точки зрения игры на органе: каким образом осуществляется управление звучанием множества труб в большом органе. Основной механизм этого управления прост и напоминает ряды и колонки матрицы. Трубы, располагаемые по регистрам, соответствуют рядам матрицы. Все трубы одного регистра обладают одним тембром, и каждая труба соответствует одной ноте на ручной или ножной клавиатуре. Подача воздуха к трубам каждого регистра регулируется специальным рычагом, на котором указано название регистра, а подача воздуха непосредственно к трубам, связанным с данной нотой н составляющим колонку матрицы, регулируется соответствующей клавишей на клавиатуре. Труба будет звучать лишь в том случае, если передвинут рычажок регистра, в котором она находится, и нажата нужная клавиша.
Размещение органных труб напоминает ряды и колонки матрицы. На этой упрощённой схеме каждый ряд, именуемый регистром, состоит из однотипных труб, каждая из которых производит одну ноту (верхняя часть схемы). Каждая колонка, связанная с одной нотой на клавиатуре (нижняя часть схемы), включает трубы разных типов (левая часть схемы). Рычажком на консоли (правая часть схемы) обеспечивается доступ воздуха ко всем трубам регистра, а нажатием клавиши на клавиатуре воздух нагнетается во все трубы данной ноты. Доступ воздуха в трубу возможен только при одновременном включении ряда и колонки.
В наше время можно применять самые различные способы осуществления подобной схемы с использованием цифровых логических устройств и электрически управляемых клапанов на каждой трубе. На старых органах использовались простые механические рычажки и пластинчатые клапаны для подачи воздуха в клавишные каналы и механические ползуны с отверстиями для управления поступлением воздуха к целому регистру. Эта простая и надёжная механическая система, помимо своих конструктивных достоинств, позволяла органисту самому регулировать скорость открытия всех клапанов и как бы делала ему более близким этот уж слишком механический музыкальный инструмент.
В XIX в начале XX в. строились большие органы со всевозможными электромеханическими и электропневматическим устройствами, но в последнее время предпочтение опять отдаётся механическим передачам от клавиш и педалей, а сложные электронные устройства используются для одновременного включения сочетаний регистров во время игры на органе. Например, самый большой орган в мире с механической передачей был установлен в концертном зале Сиднейского оперного театра в 1979 г. В нем 10500 труб в 205 регистрах, распределённых между пятью ручными и одной ножной клавиатурами. Клавишное управление осуществляется механическим способом, но оно дублируется электрической передачей, к которой можно подключаться. Благодаря этому исполнение органиста может быть записано в кодированной цифровой форме, которую затем можно использовать для автоматического воспроизведения на органе первоначального исполнения. Управление регистрами и их сочетаниями осуществляется с помощью электрических или электропневматических устройств и микропроцессоров с памятью, что позволяет широко варьировать управляющую программу. Таким образом, великолепное богатое звучание величественного органа создаётся сочетанием самых передовых достижений современной техники и традиционных приёмов и принципов, которые на протяжении многих столетий использовались мастерами прошлого.
Источник