Звукоизвлечение на классической гитаре
| автор Джон Тэйлор |
Глава 1. Музыкальный звук
1.1 Музыкальные и физические термины
Если попросить музыканта перечислить свойства отдельной ноты, сыгранной на каком-либо инструменте, то он, скорее всего, приведет следующие: высота, качество, громкость, продолжительность, атака, затухание, вибрато. Каждое из перечисленных свойств имеет свой физический эквивалент и, в принципе, может быть измерено.
Извлечение ноты на инструменте вызывает быстро чередующиеся колебания давления окружающего воздуха. Эти колебания давления, распространяющиеся в пространстве как звуковые волны, вызывают соответствующие колебания барабанной перепонки. С точки зрения физика, физические свойства этих колебаний определяют звучание ноты в понятных ему терминах
Нижеприведенное представляет собой краткое описание связи между некоторыми основными физическими величинами и эквивалентными им музыкальными свойствами. Мы пренебрегаем такими «усложнениями», вытекающими из особенностей слухового восприятия, как преобразование колебаний барабанной перепонки в электрические сигналы и интерпретация их головным мозгом. Также мы не будем пытаться затронуть все факторы звучания ноты. Цель этой главы … ввести читателя без предварительных знаний музыкальной акустики в курс дела для лучшего понимания остальной части данной книги.
1.2 Высота тона: частота
Музыкальный звук отличается от шума тем, что форма его колебаний представляет не случайный набор пиков и провалов, а закономерную периодичную последовательность. Количество колебаний в секунду называется частотой и измеряется в Герцах (Гц). Диапазон частот, различаемых средним человеческим ухом, лежит где-то в диапазоне от 20 Гц до 20 КГц. С повышением частоты повышается и высота тона, с понижением она уменьшается. На Рис. 1.1 показаны некоторые ноты на гитаре вместе с соответствующими им частотами. Частоты нот рассчитаны для равномерно темперированной шкалы (см. раздел 2.5). Частоты, большие 100 Гц, округлены до ближайшего целого.
Рис. 1.1 Частоты некоторых нот гитары
Музыкальный интервал между двумя нотами характеризуется не разностью, а отношением соответствующих нотам частот. Например, нота Ре (147 Гц) находится на чистую кварту выше ноты Ля (110 Гц) и на ту же чистую кварту ниже ноты Соль (196 Гц). Очевидно, что разность 196-147 не равна 147-110, но отношения 196/147 и 147/110 очень близки к 4/3. Читатель может проверить, что все приведенные в примере интервалы, дающие чистую кварту, имеют одинаковое отношение частот.
Наиболее простое отношение частот имеют ноты, отстоящие друг от друга на октаву: это соотношение в точности равно 2 к 1. Соответственно, ноты, отстоящие друг от друга на две октавы, имеют соотношение частот 4/1, на три октавы … 8/1 и т.д. Упомянутый выше диапазон, который воспринимает человеческий слух, покрывает чуть меньше 10 октав, что дает нам соотношение частот между крайними звуками этого диапазона примерно 1000 к 1.
Прямая связь между нотой и ее частотой пригодится нам в следующих главах. Читатель может потратить некоторое время для исследования рис 1.1 и рассчитать соотношения частот для других интервалов (например, чистой квинты и большой терции), что пригодится в дальнейшем.
1.3 Качество звучания: смесь частотных компонентов
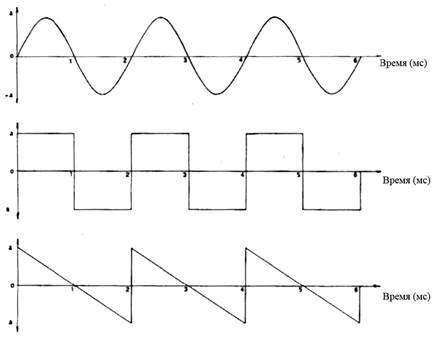
Мы заметили, что волновая форма музыкального звука повторяется во времени с определенной частотой. На Рис. 1.2 показаны 3 различных формы волны, которые несложно сгенерировать электрическим генератором волн. Каждый график представляет собой небольшой участок непрерывных колебаний. Горизонтальная ось графика поделена на равные отрезки, обозначающие тысячные доли секунды (миллисекунды). Изменения давления около среднего значения отмечаются расстояниями выше и ниже оси времени. В каждом из случаев полный цикл длится 2 миллисекунды, что соответствует частоте 500 Гц. Амплитуды в каждом цикле также равны в любой момент времени.
Рис. 1.2 Три различные формы волны
Любой, кто использовал синтезатор, знает, что эти три типа волн дают звуки совершенно разных качеств. По сравнению с пронзительным звучанием пилообразной волны, синусоида звучит гладкой, но бесхарактерной и скучной. Точно так же, два различных инструмента, играющих одну и ту же ноту с одинаковой динамикой будут звучать поразному. Эти различия в качестве вызваны различиями в формах волн, которые производят эти инструменты.
Анализ различных форм волны зависит от очень важного математического принципа: любая сложная форма волны может рассматриваться как совокупность ряда простых волновых форм. При этом сложная форма получается сложением простых волн. Достаточно легко представить, что при сложении двух волн с одинаковой частотой получится волна с той же частотой. Также легко показать, что если к волне прибавить волну с удвоенной (вообще говоря, умноженной на любое целое положительное число) частотой, то результирующая волна изменит форму, но не изменит период колебаний. Если, например, к волне с частотой колебаний в 100 Гц прибавить волны с частотами 200, 300, 400 и т.д., то результирующая волна имеет частоту те же 100 Гц.
Вообще, любую форму регулярно повторяющейся волны можно рассматривать как суперпозицию волн, частоты которых связаны именно таким способом. Единственное исключение … синусоида, которая состоит только из одной частоты. По этой же причине синусоиды называются простыми звуками (тонами) и рассматриваются как окончательно-неделимые «строительные блоки» сложной волны. Такие синусоидальные компоненты, частоты которых … точные кратные числа от фундаментальной частоты, называют гармоническими обертонами, или просто обертонами (или гармониками).
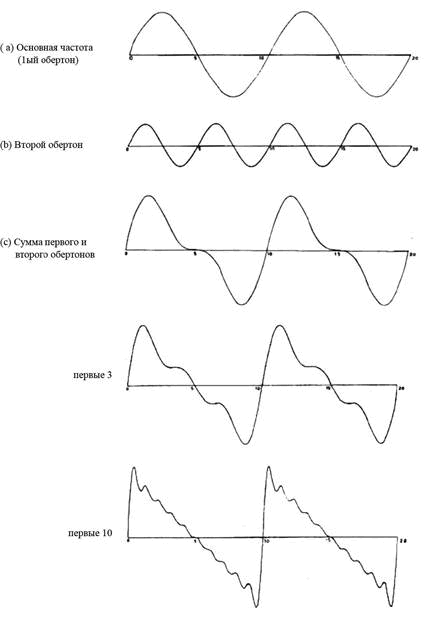
На Рис. 1.3 показан пример синтеза волны из простых тонов. Первый обертон (основной тон) имеет частоту 100 Гц, второй обертон имеет половину амплитуды основного тона и удвоенную частоту. При сложении этих двух волн (a) и (b) получается новая волна (c) с той же частотой повторений, как и у основного тона.
Рис. 1.3 Синтез пилообразной волны
Добавление третьей волны с частотой 300 Гц и 1/3 величины амплитуды основного тона дает форму волны (d). Если продолжить добавлять волны с частотами 400, 500 и т.д. и, соответственно, с амплитудами 1/4, 1/5,ѓ от амплитуды основной волны, то результат будет все больше и больше напоминать пилообразную форму, показанную на Рис. 1.2. Сумма первых десяти волн обертонов показана на Рис. 1.3. Сумма первых ста обертонов дает уже сносный результат, но все еще не точный, так как синусоида не имеет острых узлов, подобных «зубам» пилы. Теоретически для точного синтеза пилообразной волны потребовалось бы бесконечное количество обертонов. Однако острые углы вызывают резкие (неприятные) изменения звучания и практически не встречаются в природе. (Электронные синтезаторы обычно немного сглаживают углы, чтобы избежать резкого звука). Количество обертонов при извлечении на гитаре одиночного звука измеряется скорее десятками, чем сотнями.
Пронзительное звучание пилообразной волны связано с более или менее острыми углами и недостатком симметрии формы волны по сравнению с формой простого тона. Другими словами, для получения таких характеристик звука необходимы все возможные обертоны, с частотами, простирающимися по нескольким октавам. Пронзительность проявляется из-за присутствия большого количества обертонов с заметными амплитудами.
Конечно, музыкальная волна не обязательно должна содержать все возможные обертоны. (Волна, например, может быть сформирована только из обертонов с нечетными номерами). Сам основной тон может даже отсутствовать; если присутствует достаточное количество его обертонов, то ухо само «добавляет» недостающее и легко определяет высоту тона такого звука. Однако отсутствие основного тона проявляется в недостатке полноты звука. Ярким примером такого явления является прослушивание игры контрабаса, основные частоты нот которого лежат около 50 Гц, на транзисторном приемнике, динамик которого не реагирует на частоты ниже 200 Гц. В этом случае слышны только обертоны от четвертого и выше, но, несмотря на это, ухо определяет высоту тона равной основному, только звук кажется неестественно писклявым.
Не существует специальной системы словесного описания качества звука, кроме того, используемые слова сами по себе не музыкальной природы. («Яркий», «тусклый», «темный», «теплый», «округлый», «жесткий» и т.д.) Также верно и то, что слов не хватает, чтобы описать все бесконечное многообразие музыкальных звуков. Однако мы все же будем использовать множество описательных слов, чтобы примерно описывать смесь обертонов в звучании.
«Плотность» связывают с присутствием в звуке основного тона и низких обертонов, «блеск» … с присутствием некоторых высоких обертонов. Если высокие обертоны выделяются сильнее, звук может стать «жестким» и «колким/острым», если же высокие подавлены, то звучание может измениться от «округлого» и «теплого» к «толстому» и «тусклому». Если низкие обертоны слабы, звучание будет «тонким».
Кроме этих общих тенденций, каждый обертон передает свой собственный специфический аромат, который связан с его музыкальным интервалом выше основного тона. Многие из высоких обертонов, начиная с седьмого, производят диссонансные интервалы, и это, как полагают, является причиной резкости звучания, которую они создают. Интервалы между обертонами будут рассматриваться в следующей главе.
1.4 Громкость: амплитуда
Так как звук переносится изменениями давления воздуха, то кажется очевидным, что громкость звука напрямую связана с амплитудой колебаний давления. Верно, что, если прочие параметры формы волны остаются неизменными, то увеличение амплитуды увеличивает громкость. Однако если менять частота даже простого тона, восприятие громкости изменяется сложным образом и зависит как от амплитуды, так и от частоты; в случае звучания смеси обертонов расчеты громкости еще больше усложняются. Глубокое изучение таких свойств выходит за рамки данной книги, но мы все же затронем некоторые моменты, в связи с тем, что умение управлять широким динамическим диапазоном имеет особое значение для гитариста.
Зависимость громкости от частоты исследуется с помощью простого тона постоянной мощности. Если простой тон звучит с частотой, близкой к частоте первой открытой струны (330 Гц), то с понижением частоты покажется, что громкость так же уменьшается. На частоте открытой шестой струны (82.4 Гц) громкость звука может показаться вполовину меньше, а с понижением частоты ниже примерно 20 Гц звук становится неслышимым. При росте частоты от 330 Гц до примерно 1000 Гц, громкость плавно уменьшается, а затем резко возрастает, достигая своего пика в районе 3000 Гц, где громкость звука кажется удвоенной по сравнению с частотой 330 Гц. На еще более высоких частотах громкость снова уменьшается, но до 20000 Гц звуки остаются слышимы, особенно для детей и подростков. Следует четко запомнить, что человеческий слух особенно чувствителен к частотам около 3000 Гц, но заметно менее чувствителен к более высоким частотам и частотам, меньшим 100 Гц.
Если тот же самый эксперимент провести с уменьшением мощности источника звука, таким образом, что постоянная амплитуда давления уменьшается, то громкость на низких и высоких частотах снижается значительно быстрее. Если мощность источника очень мала, то любой звук с частотой менее 200 Гц будет практически неслышимым. (Вот почему некоторые усилители звука оборудованы так называемым «контуром громкости», предотвращающим исчезновение басов и низких звуков при малых уровнях громкости.)
Если регулировать мощность звукового источника, поддерживая субъективный уровень громкости на одной и той же величине, изменения мощности могут быть весьма значительными. Например, мощность звукового источника, дающая достаточно громкий звук на частоте 500 Гц, может быть увеличена стократно (соответствуя увеличению амплитуды давления в 10 раз) для создания такого же уровня громкости на частоте 50 Гц и десятикратно уменьшена для получения этого же уровня на частоте 3000 Гц. Если первоначальная мощность ниже, то соотношения могут быть еще больше. Однако эти значения необходимо рассматривать относительно исключительного диапазона слуха человека. Амплитуда давления простого тона, достаточно громкого, чтобы вызвать физическую боль может быть в миллион раз больше, чем амплитуда едва различимого тона той же частоты. Это соответствует отношению мощностей (или интенсивностей) в миллион миллионов раз к одному!
В более ограниченном диапазоне интенсивностей, в котором обычно воспринимается музыка, можно приблизительно сказать, что громкость ноты удваивается, если ее мощность увеличивается в десять раз. Именно поэтому для удвоения громкости одной скрипки требуется не две, а десять скрипок, если они будут играть в унисон. Но, по-видимому, это правило не распространяется на ноты разной частоты, так что две скрипки, играющие разные ноты, вполне могут звучать в два раза громче, чем каждая по отдельности. Что еще интереснее, обертоны отдельной ноты в этом отношении могут вести себя как разные источники звука2.
В вышеприведенной информации заключены подсказки к ответу на вопрос, почему громкость ноты может зависеть от ее качества. Например, если нижнюю Ми (82.4 Гц) извлечь таким образом, чтобы почти вся ее мощность была сосредоточена в основной частоте, то она прозвучит не очень громко по двум причинам. В первую очередь, основная частота будет звучать всего лишь в два раза громче, чем если бы на нее приходилось 10% мощности, вложенной в ноту, тогда как если ту же мощность распределить более равномерно среди, скажем, первых шести обертонов, то можно получить звук, почти в шесть раз более громкий, чем каждый из них в отдельности. Во вторых, ухо менее чувствительно к основной частоте этой ноты, чем к частотам ее высших обертонов, особенно лежащим около четвертого. Способы, которыми исполнитель может управлять относительной мощностью, которая вкладывается в различные обертоны, будут изложены позднее; кроме того, позднее будет рассмотрен также и отклик корпуса гитары … еще один существенный фактор, влияющий на громкость. В настоящий момент можно с уверенностью сказать, что если нота на гитаре должна прозвучать громко и ясно, то она должна содержать много обертонов, покрывающих широкий частотный диапазон. И наоборот, нота, имеющая «толстый» характер (то есть с подавленными высшими обертонами) вряд ли будет звучать очень громко, разве что корпус гитары будет особенно восприимчив к основной частоте этой ноты.
В пункте (b) содержится объяснение еще одной известной характеристики гитары … она слабо звучит, если играть на ней слишком мягко. Это относится ко многим инструментам, но небольшая мощность и относительно низкий регистр гитары делают ее особенно восприимчивой к этой проблеме. Аналогично, любой инструмент звучит слабо на некотором удалении, но гитару на дальнем конце очень большого помещения будет простонапросто не слышно. В этом случае хорошо слышными будут только те обертоны, которые лежат в частотном диапазоне примерно от 1000 до 5000 Гц; однако акустические свойства помещения могут влиять на звук множеством способов3.
Это всего лишь некоторые из интересных гитаристу выводов касательно факторов, влияющих на громкость. Читатель может вспомнить другие факторы, применимые к конкретным музыкальным ситуациям, однако даже простое знание о разнообразии вовлеченных факторов, без подробных знаний о каждом из них, может быть полезно в том смысле, что поможет ему поверить своим ушам. Управление динамикой это нечто большее, чем игра с большим или меньшим усилием, и динамические контрасты, достигаемые изменением качества звука, а не его общей мощностью, не менее реальны и могут быть столь же эффективны.
1.5 Атака, затухание и вибрато
В объяснении качества звука, изложенном в разделе 1.3 использовалось чрезвычайно упрощающее предположение о том, что форма волны музыкального звука должна всегда в точности повторяться. Однако это невыполнимо во время звучания нот, сыгранных на любом реальном инструменте. В этом разделе будут рассмотрены некоторые из отклонений от равномерности, которые увеличивают интересность ноты4.
Устойчивые колебания никогда не начинаются мгновенно, а требуют некоторого времени для нарастания. Гитара имеет необычно быструю атаку, но практически никогда не достигает устойчивых колебаний, потому что каждая нота начинает затухать, как только достигается полная амплитуда. Однако эти факты не противоречат теории о том, что тембр инструмента зависит от конкретной суммы обертонов. Одно время существовала идея о том, что можно электронно синтезировать звуки инструментов, наложив подходящие характеристики атаки и затухания на форму волны, созданную сложением синусоидальных волн в нужной пропорции. Но такие синтезированные звуки не могли обмануть слух ни на секунду, что позволяет предположить, что звук музыкального инструмента это нечто большее.
В последнее время распространяется понимание того, что нерегулярное поведение в начале ноты, называемое стартовым переходом, является такой же характеристикой инструмента, как и устойчивые колебания, которые следуют за ним. Стартовые переходы возникают в основном от взаимодействия между различными деталями инструмента. Гитара, например, состоит из двух зависимых вибраторов … струны и корпуса. Сама по себе струна колебалась бы более или мене регулярно с момента высвобождения, но для получения звука ее колебания должны быть переданы корпусу. Корпус, имеющий свои отдельные собственные формы колебаний, не начинает мгновенно колебаться вместе со струной, а сначала сложным образом откликается на воздействие, что вызывает стартовый переход.
Существует несколько способов изучения стартовых переходов5, особенно поразительным является метод записи ноты на пленку, после чего часть пленки, содержащая стартовый переход, вырезается. Изменения звука, вносимые этой процедурой, могут быть впечатляющи, и уже будет не так просто определить инструмент (можно легко спутать виолончель и фагот, или кларнет и гобой). Я слышал записи нот, сыгранных на гитаре, у которых была отрезана начальная десятая доля секунды, и получившиеся звуки напоминали более синтезатор, нежели любой реальный инструмент, однако их характер, тем не менее, значительно менялся при изменении положения точки защипывания на струне.
В общем случае ноты звучат намного более интересно со стартовым переходом, чем без него. Это еще раз подтверждает общий принцип, заключающийся в том, что слуху предпочтительнее некоторая степень вариации, чем точное повторение, даже во время звучания одной ноты. Нота, сыгранная на гитаре, неизбежно изменяется за время звучания, не только по громкости, но также и по характеру, так как разные обертоны затухают с различными скоростями.
Гитара далеко не единственный инструмент, который производит звуки, постепенно затухающие и изменяющиеся во время звучания. Что отличает ее от таких инструментов как фортепиано, клавесин и арфа, так это возможность выполнять вибрато. Так называется периодическое изменение высоты ноты (то есть ее основной частоты), хотя амплитуда и характер также могут изменяться в некоторой степени. Исследования показали, что хорошие оркестровые музыканты предпочитают скорость вибрато 6 или 7 Гц, что, весьма неожиданно, совпадает с естественной скоростью, с которой певцы модулируют голос6. Вероятно, вибрато приятно слуху потому, что оно вносит человеческие качества в звук инструмента. Диапазон изменения высоты обычно составляет четверть тона в каждую сторону у певцов, и вполовину меньше у скрипачей он. «Размах» вибрато в значительной степени зависит от вкуса и моды. Излишнее вибрато воспринимается как одна из отвратительнейших вещей; тем не менее, считается, что вибрато примерно оптимальной частоты и умеренного размаха вообще не воспринимается как изменение высоты, но ощущается как появление в звуке «жизненности», «теплоты» или «силы». Однако не стоит думать, что существуют единственные и неизменные оптимальные скорость и размах для вибрато. Необходимо помнить, что постоянное и не изменяющееся вибрато (как у электрооргана) для человеческого слуха может звучать практически также скучно и неестественно, как полное его отсутствие. Принцип изменения применим здесь в той же мере, и при игре на гитаре может быть особенно эффективными усиливать ноту с помощью вибрато после того, как она начала звучать. Многие считают гибкое и изобретательное использование вибрато наиболее ценным инструментом гитариста для придания звуку окраски и выразительности.
Источник